正则化
regularization
在介绍Ridge和Lasso回归之前,我们先了解一下正则化
过拟合和欠拟合
(1) under fit:还没有拟合到位,训练集和测试集的准确率都还没有到达最高。学的还不 到位。
(2) over fit:拟合过度,训练集的准确率升高的同时,测试集的准确率反而降低。学的过 度了,做过的卷子都能再次答对,考试碰到新的没见过的题就考不好。
(3) just right:过拟合前训练集和测试集准确率都达到最高时刻。学习并不需要花费很多 时间,理解的很好,考试的时候可以很好的把知识举一反三。真正工作中我们是奔着过 拟合的状态去调的,但是最后要的模型肯定是没有过拟合的。
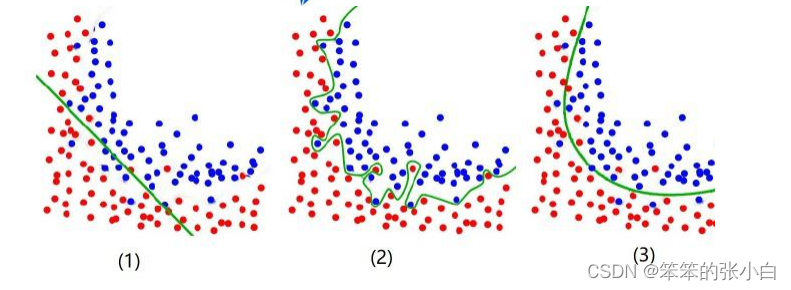
正则化就是防止过拟合,增加模型的鲁棒性 robust,鲁棒是 Robust 的音译,也就是 强壮的意思。就像计算机软件在面临攻击、网络过载等情况下能够不死机不崩溃,这就是该 软件的鲁棒性。鲁棒性调优就是让模型拥有更好的鲁棒性,也就是让模型的泛化能力和推广 能力更加的强大。举以下例子:下面两个式子描述同一条直线那个更好?
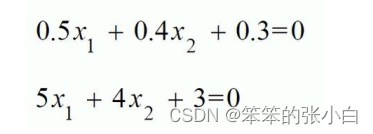
第一个更好,因为下面的公式是上面的十倍,当 w 越小公式的容错的能力就越好。因 为把测试集带入公式中如果测试集原来是 100 在带入的时候发生了一些偏差,比如说变成 了 101,第二个模型结果就会比第一个模型结果的偏差大的多。公式中 y w x T = ^ 当 x 有一点 错误,这个错误会通过 w 放大从而影响 z。但是 w 不能太小,当 w 太小时正确率就无法保 证,就没法做分类。想要有一定的容错率又要保证正确率就要由正则项来决定。
所以正则化(鲁棒性调优)的本质就是牺牲模型在训练集上的正确率来提高推广能力, W 在数值上越小越好,这样能抵抗数值的扰动。同时为了保证模型的正确率 W 又不能极小。 故而人们将原来的损失函数加上一个惩罚项,这里面损失函数就是原来固有的损失函数,比 如回归的话通常是 MSE,分类的话通常是 cross entropy 交叉熵,然后在加上一部分惩罚 项来使得计算出来的模型 W 相对小一些来带来泛化能力。
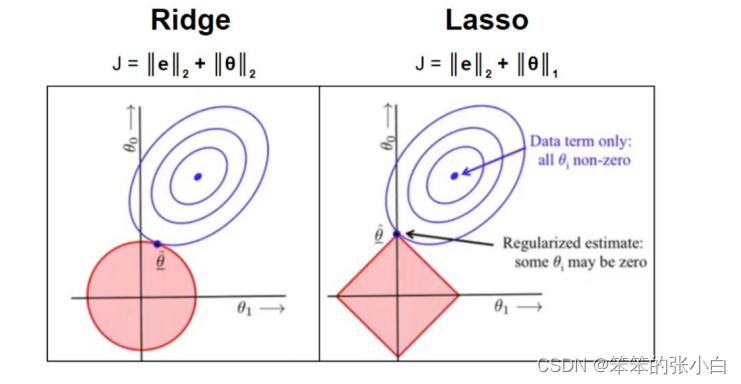
常用的惩罚项有 L1 正则项或者 L2 正则项:

其实 L1 和 L2 正则的公式数学里面的意义就是范数,代表空间中向量到原点的距离。
当我们把多元线性回归损失函数加上 L2 正则的时候,就诞生了 Ridge 岭回归。当我们 把多元线性回归损失函数加上 L1 正则的时候,就孕育出来了 Lasso 回归。其实 L1 和 L2 正 则项惩罚项可以加到任何算法的损失函数上面去提高计算出来模型的泛化能力的。
Ridge 回归
代码实现
# 同样从 sklearn.linear_model 下导入
import numpy as np
from sklearn.linear_model import Ridge# 创建 X,y 数据
X = 2*np.random.rand(100, 1)
y = 4 + 3*X + np.random.randn(100, 1)# 调用模型
ridge_reg = Ridge(alpha=0.4, solver='sag')
ridge_reg.fit(X, y)
print(ridge_reg.predict([[1.5]])) # 带入数据进行结果预测
print(ridge_reg.intercept_) # 截距
print(ridge_reg.coef_) # 系数[[8.6487326]]
[4.11689518]
[[3.02122495]]这里 alpha 设置为 0.4 对应的就是公式中的α正则项系数,solver=’sag’就是使用随机梯 度下降法来求解最优解
源码解析
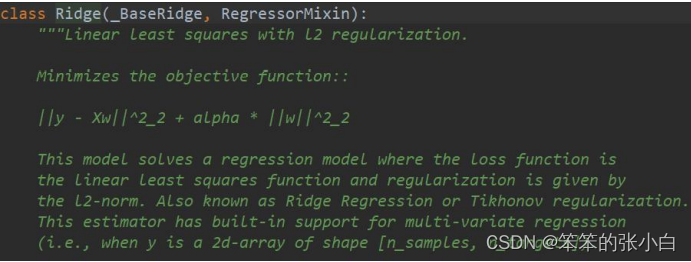
alpha:正则项系数
fit_intercept:是否计算 W0 截距项
normalize:是否做归一化
max_iter:最大迭代次数
solver:优化算法的选择
使用SGDRegressor实现同样的算法
# 同样从 sklearn.linear_model 下导入
import numpy as np
from sklearn.linear_model import SGDRegressor# 创建 X,y 数据
X = 2*np.random.rand(100, 1)
y = 4 + 3*X + np.random.randn(100, 1)# 调用模型
sgd_reg = SGDRegressor(penalty='l2', max_iter=10000)
sgd_reg.fit(X, y.reshape(-1,))
print(sgd_reg.predict([[1.5]]))
print(sgd_reg.intercept_)
print(sgd_reg.coef_)[8.45801805]
[3.5372549]
[3.28050876]Lasso 回归
代码实现
import numpy as np
from sklearn.linear_model import Lasso
# 创建数据集
X = 2*np.random.rand(100, 1)
y = 4 + 3*X + np.random.randn(100, 1)
# 调用模型
lasso_reg = Lasso(alpha=0.01, max_iter=30000)
lasso_reg.fit(X, y)
# 打印结果
print(lasso_reg.predict([[1.5]])) # 带入数据进行预测
print(lasso_reg.intercept_) # 截距
print(lasso_reg.coef_) # 系数[8.46496349]
[3.93328286]
[3.02112042]使用SGDRegressor实现同样的算法
import numpy as np
from sklearn.linear_model import Lasso
from sklearn.linear_model import SGDRegressorX = 2*np.random.rand(100, 1)
y = 4 + 3*X + np.random.randn(100, 1)sgd_reg = SGDRegressor(penalty='l1', max_iter=10000)
sgd_reg.fit(X, y.ravel())
print(sgd_reg.predict([[1.5]]))
print(sgd_reg.intercept_)
print(sgd_reg.coef_)
[8.4622419]
[3.62090517]
[3.22755782]这里 ravel()操作是扁平化
eg:



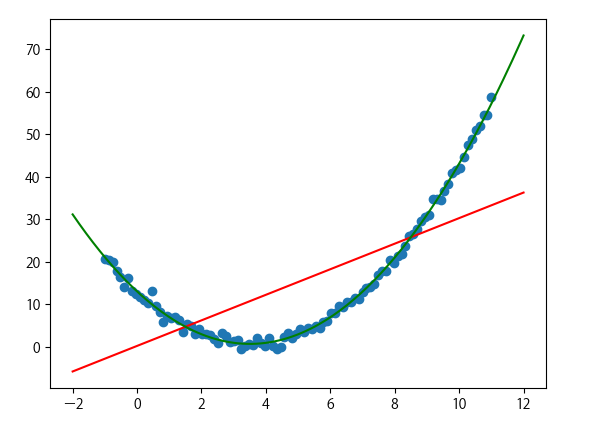






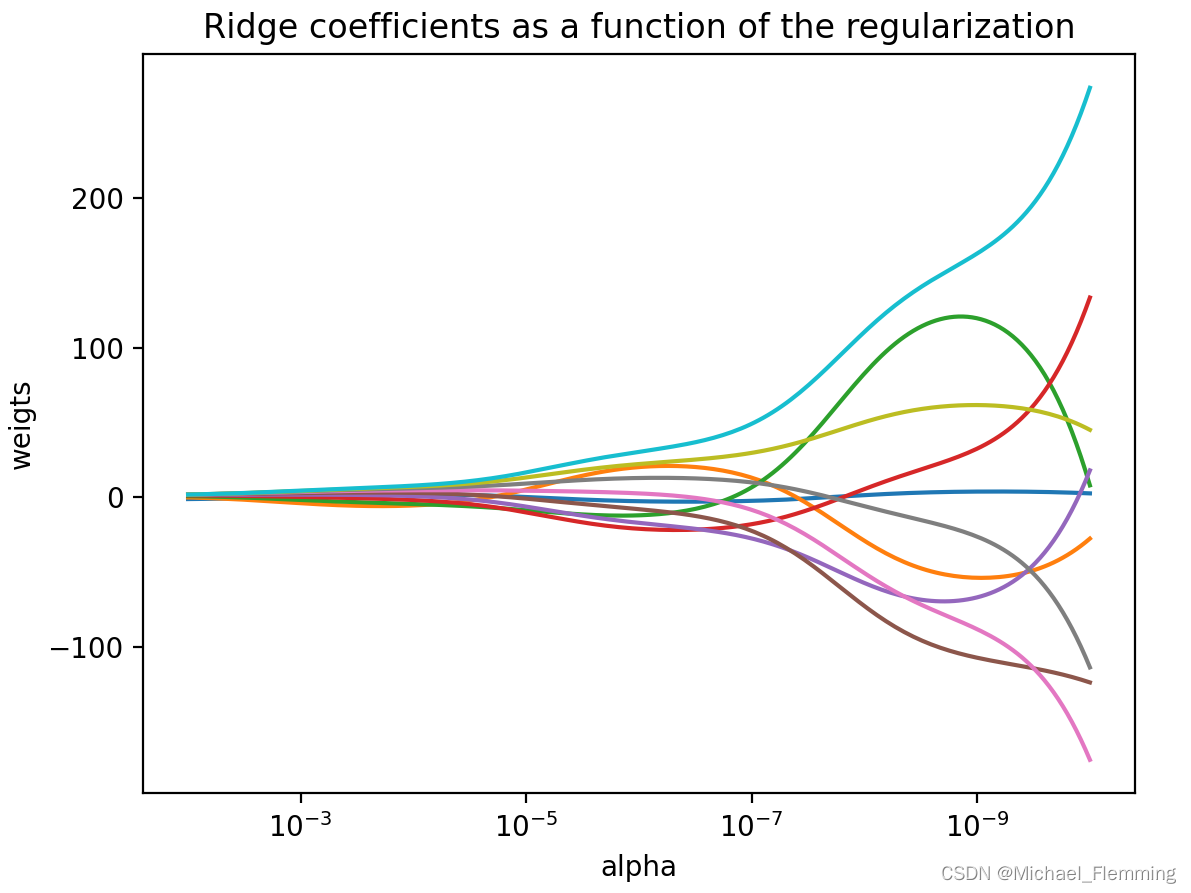
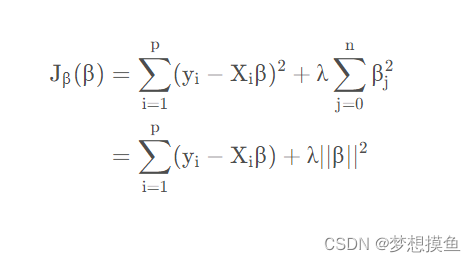


![[组原]初识-地址总线,地址寄存器,存储单元,存储字长](https://img-blog.csdnimg.cn/fec3f6f79ccb4139a78eac6fde3ece22.png)