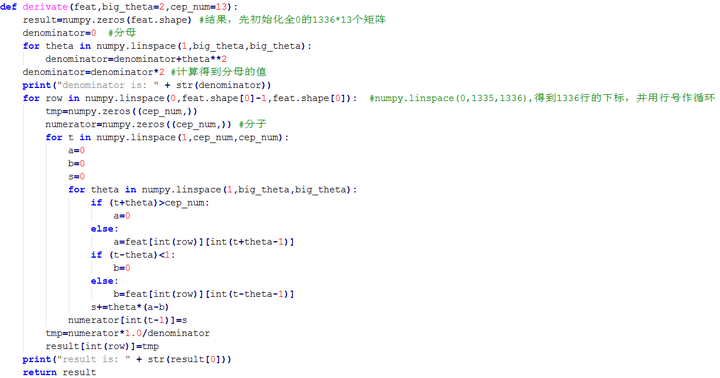
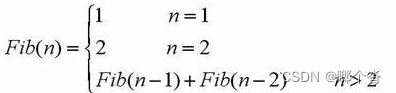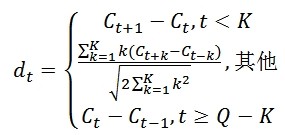斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……。在数学上，斐波那契数列以如下被以递推的方法定义：F(1)=1, F(2)=1, F(n)=F(n - 1)+F(n - 2)（n ≥3，n ∈ N*），我们用C语言来实现它： 

最不适用于用递归函数的经典题目：斐波那契数列

第一种 递归法：斐波那契数列的规律为：Fibon(n) = Fibon(n-1) + Fibon(n-2)  

 我们先看一个求位数少的（代码1），这个很快就算出来了。再看一个位数多的（代码2）

代码1：

#include<stdio.h>
int Fibon(int n)
{if (n == 1|| n == 2){return 1;}else{return Fibon(n-1)+ Fibon(n-2);}
}
int main()
{for (int i = 1; i <= 10; i++){printf("%d ", Fibon(i));}return 0;
}

调试结果：

代码2：

#include<stdio.h>
int Fibon(int n)
{if (n == 1|| n == 2){return 1;}else{return Fibon(n-1)+ Fibon(n-2);}
}
int main()
{for (int i = 1; i <= 40; i++){printf("%d ", Fibon(i));}return 0;
}

调试结果如下：

此时的结果就出的很慢，原因是什么？因为它超出堆栈的默认1MB的大小所以就结果出的很慢。

对于斐波那契数列我们最好还是使用for循环来写。

第二种 for 循环：（简单高效）

#include<stdio.h>
int Fibon1(int n)
{int f1 = 1;//1//2int f2 = 1;//2//3int f3 = 1;//2//3for(int i=2; i<n; i++){f3 = f1+f2;f1 = f2;f2 = f3;}return f3;
}
int main()
{for (int i = 1; i <= 10; i++){printf("%d ", Fibon1(i));}return 0;
}

调试结果如下：只要求的斐波那契数超过40，for循环都可一瞬，而递归的方法就会慢很多。