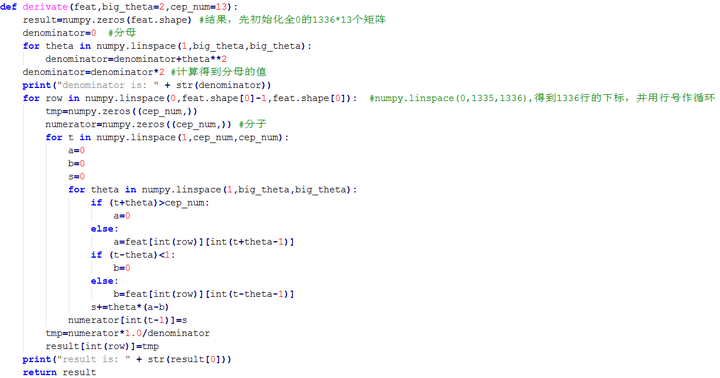
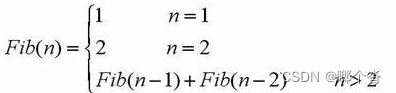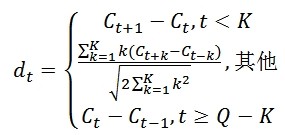1. 定义：

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、55、...... 这个数列从第3项开始，每一项都等于前两项之和。

2. 求第n个斐波那契数的方法：

（1）递归

#include<stdio.h>
int Fib(int n)
{if (n <= 2){return 1;}else{return Fib(n - 1) + Fib(n - 2);}
}
int main()
{int n = 0;printf("input n: ");scanf("%d", &n);printf("%d\n",Fib(n));return 0;
}

我们输入50，看一下第50个斐波那契数是什么

可以看见，光标一直在闪，说明程序是一直在执行的状态，但是没有输出结果，这是为什么呢？

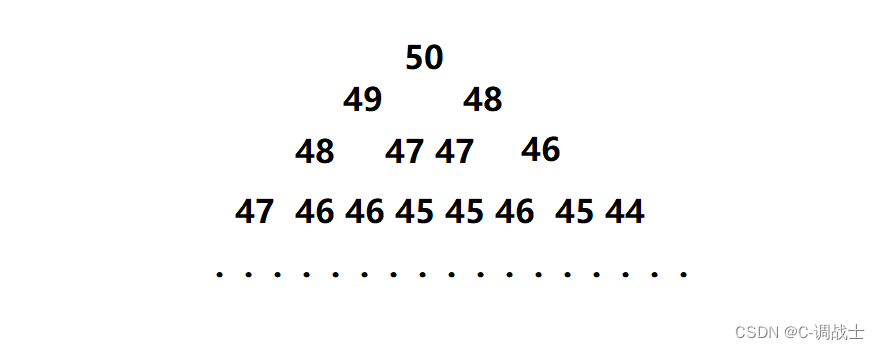
 可见，重复计算的数有很多，是个不小的工程量，我们可以计算一下某个斐波那契数被重复计算的次数

统计一下计算第40个斐波那契数时第3个斐波那契数被重复计算的次数（代码如下）：

//递归法
#include<stdio.h>
int count = 0;//全局变量int Fib(int n)
{//统计的是 第3个斐波那契数被重复计算的次数if (3 == n){count++;}if (n <= 2){return 1;}else{return Fib(n - 1) + Fib(n - 2);}
}
int main()
{int n = 0;printf("input n: ");scanf("%d", &n);printf("%d\n",Fib(n));printf("count= %d\n", count);return 0;
}

 由此可见，计算机的计算量非常大，时间复杂度和空间复杂度都极高，很容易造成栈溢出和超时。所以这里使用递归显然不是一个明智的选择。

（2）迭代

//迭代法
#include<stdio.h>
int Fib(int n)
{int a = 1;int b = 1;int c = 1;while (n>2){c = a + b;a = b;b = c;n--;}return c;
}
int main()
{int n = 0;printf("input n: ");scanf("%d", &n);printf("%d\n",Fib(n));return 0;
}

循环迭代方法的效率大大高于递归，只是相比于递归代码可读性稍微差一些。

3. 提示：

（1）许多问题是以递归的形式进行解释的，这只是因为它们比非递归的形式更为清晰。

（2）但是这些问题的迭代实现往往比递归实现效率更高，虽然代码的可读性稍微差一些。

（3）当一个问题相当复杂，难以用迭代实现时，此时递归实现的简洁性便可以补偿它所带来的运行时的开销。