1.质数：又称素数。是一个大于1的自然数（最小质数为2）。除了1和它自身外，不能被其他自然数整除的数。
=>质数：用n除[2,n-1]的所有数,不能整除就是n就是质数。

2.[2,n-1]缩小到[2,√n]效果相同

原因：判断一个n（n>1，自然数）是否是质数？
n=xy，x、y为整数，n=√n√n，此时就当x，y都等于√n，x取小于√n的某整数时，若能被n整除，得到y大于√n的某整数，也能被n整除，保持乘积还是n。x、y两个约数在√n两边。判断是否素数，需要n除[2,n-1]的所有数，使用√n分为[2,√n]和[√n,n-1]，n在[2,√n]有约数，在[√n,n-1]也有约数，n在[2,√n]没有约数，在[√n,n-1]也没有约数。
其实只需要[2,√n]就能起到判断质数作用。

//求100000以内的质数？class PrimeNumberTest {public static void main(String[] args) {//方法1long start = System.currentTimeMillis(); //开始时间for(int i = 2; i<=100000; i++){if(i==2){System.out.print(i+" ");}for(int j=2; j<=i-1; j++){if(i % j != 0){//不能被整除if(j != i-1){//不是最后一个数，继续遍历continue;}else{//是最后一个数System.out.print(i+" ");}}else{//遍历过程中,只要有一个数能被整除，跳出内循环break;}}}long end = System.currentTimeMillis(); //结束时间System.out.println("消耗时间" + (end - start));System.out.println();//方法2（未优化）long start1 = System.currentTimeMillis(); for(int i=2; i<=100000; i++){boolean isFlag = true;for(int j = 2; j<=i-1; j++){if(i % j == 0){isFlag = false;}}if(isFlag == true){System.out.print(i+" ");}}long end1 = System.currentTimeMillis(); System.out.println("消耗时间" + (end1 - start1));System.out.println();//方法2（优化）long start2 = System.currentTimeMillis(); for(int i=2; i<=100000; i++){boolean isFlag = true;for(int j = 2; j<=Math.sqrt(i); j++){//优化1，对质数。[2,这个数-1]->[2,√这个数]if(i % j == 0){isFlag = false;break;//优化2，对非质数。在遍历是否整除过程中，只要出现整除的，立马终止循环，不除后续的数。}}if(isFlag == true){System.out.print(i+" ");}}long end2 = System.currentTimeMillis(); System.out.println("消耗时间" + (end2 - start2));System.out.println();//方法3long start3 = System.currentTimeMillis(); laber:for(int i=2; i<=100000; i++){//对这个for循环打个标签laberfor(int j = 2; j<=Math.sqrt(i); j++){if(i % j == 0){continue laber;//不是质数，结束外层for循环的当次循环（这个数不是质数换个数继续判断）}}//执行到此处的都是质数System.out.print(i+" ");}long end3 = System.currentTimeMillis(); System.out.println("消耗时间" + (end3 - start3));}
}

方法1：
方法2（未优化）：
方法2（优化）：
方法3：

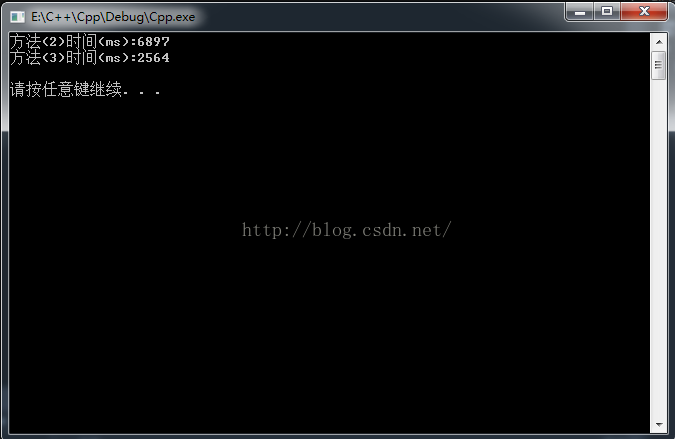
可以看出方法2（优化）执行效率最快。