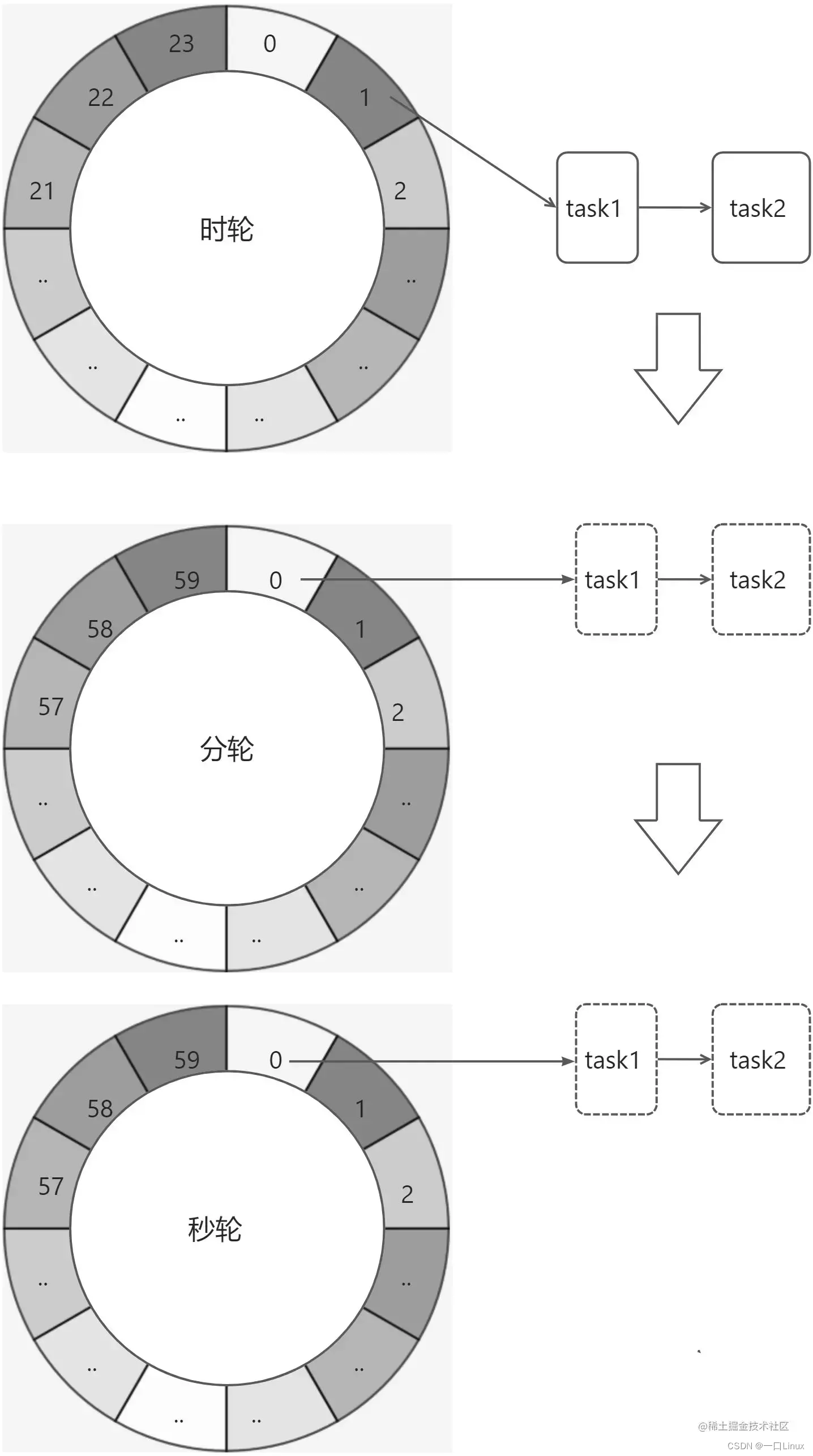
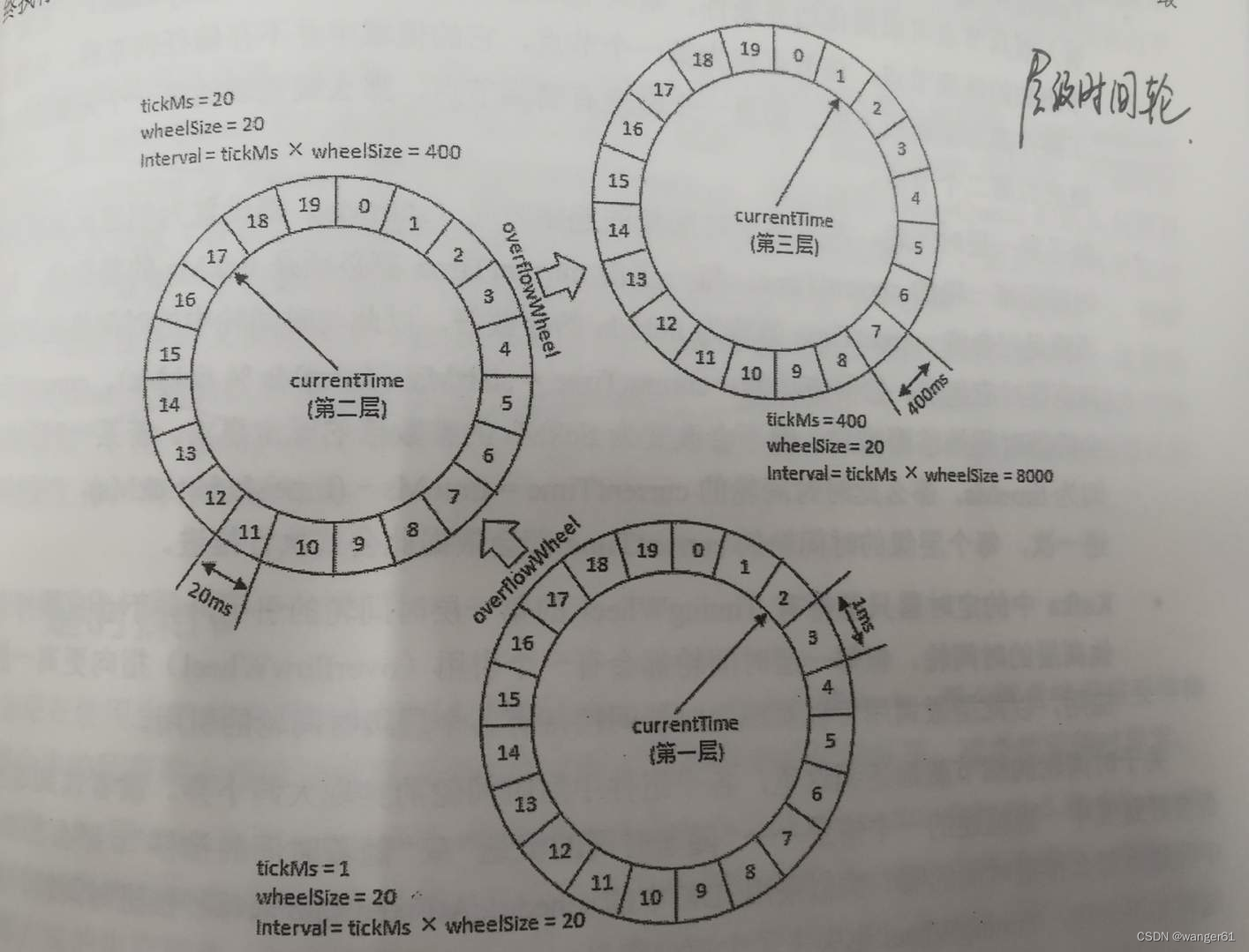
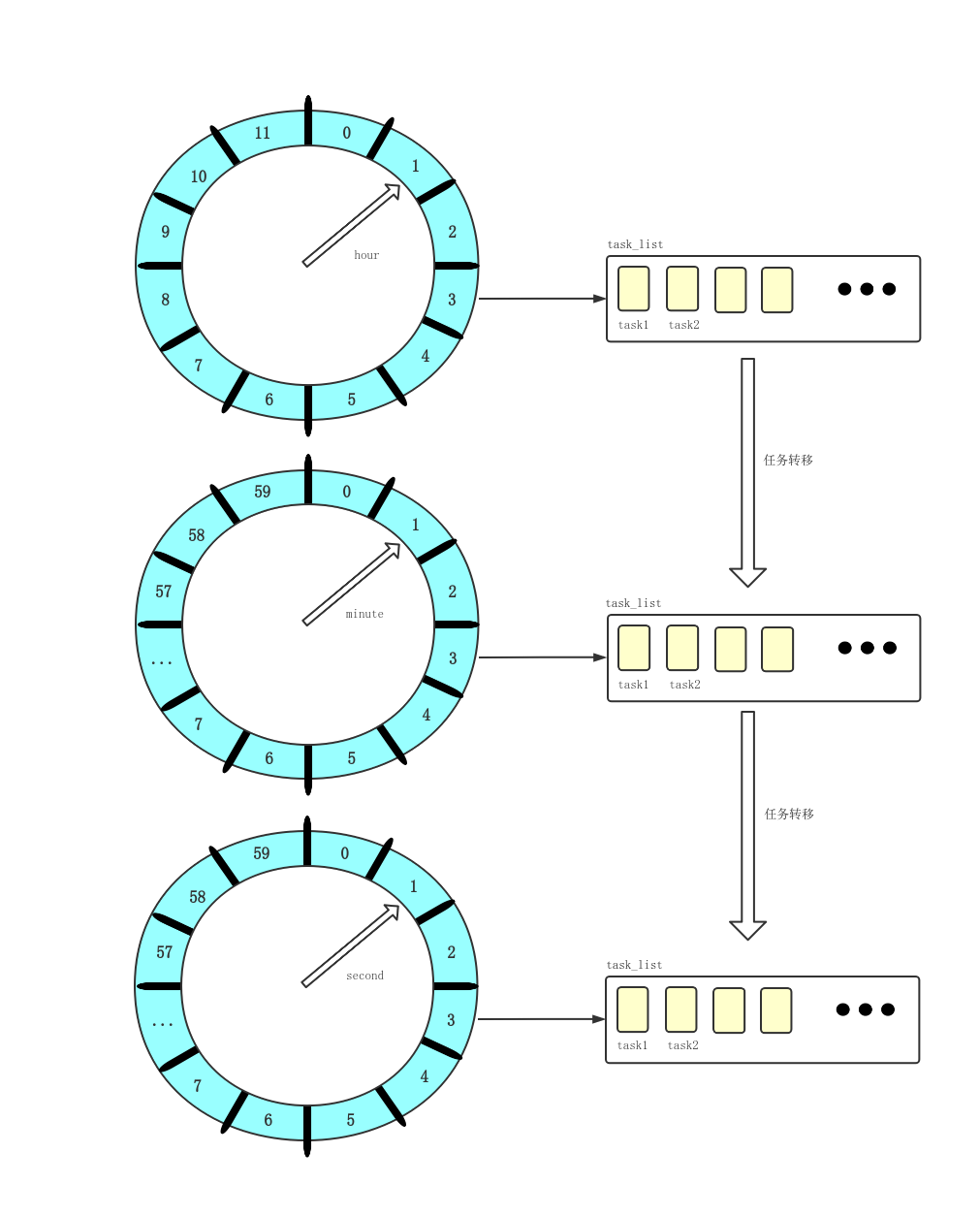
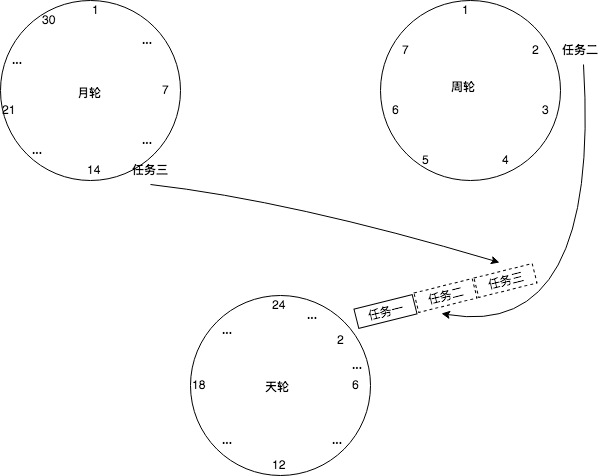
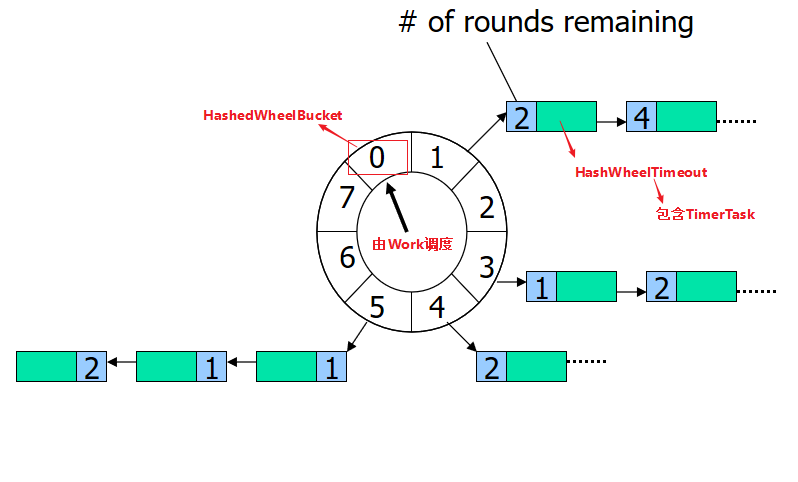
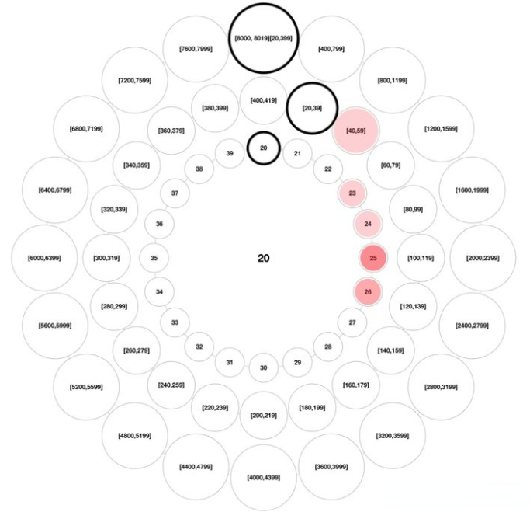
在前面的文章《时间轮-理论篇》讲了时间轮的一些理论知识，然后根据理论知识。我们自己来实现一个简单的时间轮。

1. 理论抽象

将时间轮的理论进行抽象，主要有两个方面：

• 时间轮的转动
• 每一个时间间隔任务的处理，从时间间隔的Buket中取出要执行的任务，删除已经关闭的任务。将任务提交给线程池进行执行处理

2.Java实现

接口：

public interface Timer {void createTimerTask(TimerTask task, long delay, TimeUnit unit);}public interface TimerTask {void run();}

实现类：

public class TimeWheel implements Timer {private ExecutorService service = Executors.newFixedThreadPool(Runtime.getRuntime().availableProcessors());private BlockingQueue<TimerTaskWrapper> addQueue = new ArrayBlockingQueue<>(128);//每一个tick时间间隔默认1毫秒private final long duration;//时间轮启动时间private volatile long startTime;private Thread timeWheelThread;private CountDownLatch startLatch = new CountDownLatch(1);//时间轮的tick数量private int tickNum = 128;private Bucket[] buckets;private boolean started = false;public TimeWheel(long duration, TimeUnit unit) {long nanos = unit.toNanos(duration);if (TimeUnit.MILLISECONDS.toNanos(1) > nanos) {this.duration = 1;} else {this.duration = unit.toMillis(duration);}this.timeWheelThread = new Thread(new Worker());this.buckets = new Bucket[tickNum];for (int i = 0; i < tickNum; ++i) {this.buckets[i] = new Bucket();}}@Overridepublic void createTimerTask(TimerTask task, long delay, TimeUnit unit) {start();long deadline = System.currentTimeMillis() + unit.toMillis(delay) - startTime;System.out.println("deadline="+deadline);addQueue.offer(new TimerTaskWrapper(task, deadline));}private void start() {if (started) {return;}started = true;timeWheelThread.start();try {startLatch.await();System.out.println("启动完成");} catch (Exception e) {e.printStackTrace();}}//处理时间轮的转动class Worker implements Runnable {//记录tick的次数private long tick;@Overridepublic void run() {startTime = System.currentTimeMillis();startLatch.countDown();System.out.println("Worker 启动完成..........");for (; ; ) {long time = nextTick();if (time <= 0) {continue;}int bucketIndex = (int) (tick & (tickNum - 1));System.out.println("bucketIndex="+bucketIndex);Bucket bucket = buckets[bucketIndex];//处理阻塞队列中的taskdoHandleQueneTask();//处理过期数据bucket.expire(time);tick++;}}private void doHandleQueneTask() {for (int i = 0; i < 1024; ++i) {TimerTaskWrapper taskWrapper = addQueue.poll();//队列为空if (taskWrapper == null) {break;}long taskTicks = taskWrapper.deadline / duration;taskWrapper.rounds = (taskTicks - tick) / tickNum;final long ticks = Math.max(taskTicks, tick);int bucketIndex = (int) (ticks & (tickNum - 1));System.out.println("inster bucketIndex = " + bucketIndex);Bucket bucket = buckets[bucketIndex];bucket.addTimerTask(taskWrapper);}}private long nextTick() {long deadline = duration * (tick + 1);for (; ; ) {long current = System.currentTimeMillis() - startTime;long sleepTime = deadline - current;if (sleepTime <= 0) {return current;}try {Thread.sleep(sleepTime);} catch (Exception e) {e.printStackTrace();}}}}class TimerTaskWrapper implements Runnable {private TimerTask task;//任务执行截止时间protected long deadline;//多少圈protected long rounds;TimerTaskWrapper prev;TimerTaskWrapper next;public TimerTaskWrapper(TimerTask task, long deadline) {this.task = task;this.deadline = deadline;}@Overridepublic void run() {task.run();}public void expire() {service.execute(this);}}class Bucket {TimerTaskWrapper head;TimerTaskWrapper tail;public void addTimerTask(TimerTaskWrapper task) {if (task == null) {return;}if (head == null) {tail = task;head = tail;} else {tail.next = task;task.prev = tail;tail = task;}}public TimerTaskWrapper removeTimerTask(TimerTaskWrapper task) {TimerTaskWrapper next = task.next;if (task.prev != null) {task.prev.next = next;}if (task.next != null) {task.next.prev = task.prev;}if (task == head) {if (task == tail) {head = null;tail = null;} else {head = next;}} else if (task == tail) {tail = task.prev;}task.prev = null;task.next = null;return next;}public void expire(long deadline) {TimerTaskWrapper task = head;while (task != null) {TimerTaskWrapper next = task.next;if (task.rounds <= 0) {next = removeTimerTask(task);if (task.deadline <= deadline) {task.expire();}} else {//减少时间轮的圈数task.rounds--;}task = next;}}}
}

编写一个测试案例来测试一下：

public class Test {public static void main(String[] args) {final TimeWheel wheel = new TimeWheel(1, TimeUnit.SECONDS);wheel.createTimerTask(new TimerTask() {@Overridepublic void run() {System.out.println(1111);wheel.createTimerTask(this, 4, TimeUnit.SECONDS);}}, 3,TimeUnit.SECONDS);}
}

运行打印结果：

说明：从日志的打印可以发现，在延迟三秒的情况下你会发现打印了 bucketIndex=xxx 四次。为什么会这样打印四次呢？因为当时间轮的tick在当前的时间间隔内，这个时间是不算的，从下个开始的。所以打印了四次。

3. 总结

从上面的实现可以看出来，时间间隔越长调用的就越不准确。例如刚开始的时候添加了任务到时间轮中，那么当前时间间隔就需要多消耗，实际的添加任务的执行时间为：当前时间轮剩下的时间+任务延迟执行的时间。所以如果对任务执行需要精确时间时间轮不适合。

我是蚂蚁背大象，文章对你有帮助点赞关注我，文章有不正确的地方请您斧正留言评论~谢谢！