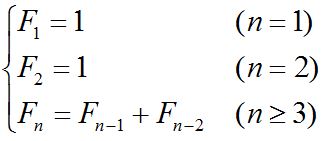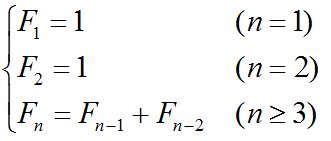时间轮算法的应用非常广泛，在 Dubbo、Netty、Kafka、ZooKeeper、Quartz 的组件中都有时间轮思想的应用，甚至在 Linux 内核中都有用到。

其思想理论基础可以参考论文：http://www.cs.columbia.edu/~nahum/w6998/papers/ton97-timing-wheels.pdf

任务队列的模型设计

实际生产中常用的消息处理组件 Kafka、Redis、MQ 都是基于消息队列的定时任务实现的。归纳来说，一个基本的任务队列模型需要能够支持依赖几个功能：

• 定时任务的添加
• 定时任务的删除/获取
• 定时任务的执行（通常将任务分配给异步线程池来处理）

一个最直接的想法是，为了方便向任务对列表添加或者删除任务，通常选择双向链表作为任务队列的数据结构。每个任务都是指定一个时间戳字段，用以标识当前任务的执行时间。此时任务队列的实现策咯为：任务队列的轮询线程不断扫描每一个任务，比较其时间戳与当前时间，判断是否达到任务的执行时刻。但是如果大部分任务都没有达到指定的执行时间，那么线程会不停地进行轮询的动态，实现效率非常差。

一种改良的方案是，每次插入定时任务时都保证队列的有序性，将任务队列升级成一个按照任务执行时间递增的有序队列。此时任务队列的执行策咯为：轮询线程从头开始遍历任务队列，发现当前任务未达到执行时间时，就可以停止遍历。甚至在时间间隔较大时，轮询线程还可以进行休眠，以避免空轮询消耗资源。但是，保证有序性需要的代价是复杂度为 O(n) 的任务插入动作，与复杂度为 O(1) 的普通任务队列插入相比，性能上有一定的牺牲。

在此基础上再加入“分而治之”的思想进行改良，我们可以将这个可能很大的任务队列拆分成多个小队列，减小有序插入定时任务时实际的性能消耗，同时采用多轮询线程的方式分别对每个队列进行遍历，这样就能将队列规模进行简化，提升任务队列处理的效率。然而多轮询线程的存在增加了CPU的系统调度，如果定时任务数量极大时，多线程轮询的方式反而降低了系统的执行效率。

上述的方案都各自有其优缺点，没有绝对正确或者错误的方案，在特定的场景中都有其适用的因素。但是在一个量级非常大的高并发场景中，我们就需要结合上述方案的长处，设计出一个充分利用时间和空间效率的任务队列算法，以达到最佳的性能效果。时间轮算法就是其中一个可选的方案。

时间轮基本方案

基于上面的分析，我们可以归纳出一个高效的定时任务队列模型需要考虑一下几个因素：

• 合理的数据结构：任务队列保证有序性的同时，还要保证轮询线程的执行效率；
• 基本的并发响应：多线程轮询可以提升任务队列的遍历效率，但数量不宜太多，避免影响系统的 CPU 性能。

时间轮就是一种高效利用线程资源的任务调度模型，把大批量的调度任务全部整合到一个调度器中，对任务进行统一的调度管理。针对诸如定时任务、延时任务、通知任务等事件的管理具有很不错的效率。

时间轮本质上是一个环形队列，底层采用了数组进行实现，数组的索引代表其参考的任务执行的时间，数组中的每个元素可以存放一个定时任务列表。定时任务列表同样是一个环状的双向链表，其中每一项代表一个可执行的定时任务项。因此，时间轮的结构可以看作是将同一时刻执行的定时任务聚合在一个任务队列中，并挂在相应时间的数组索引上

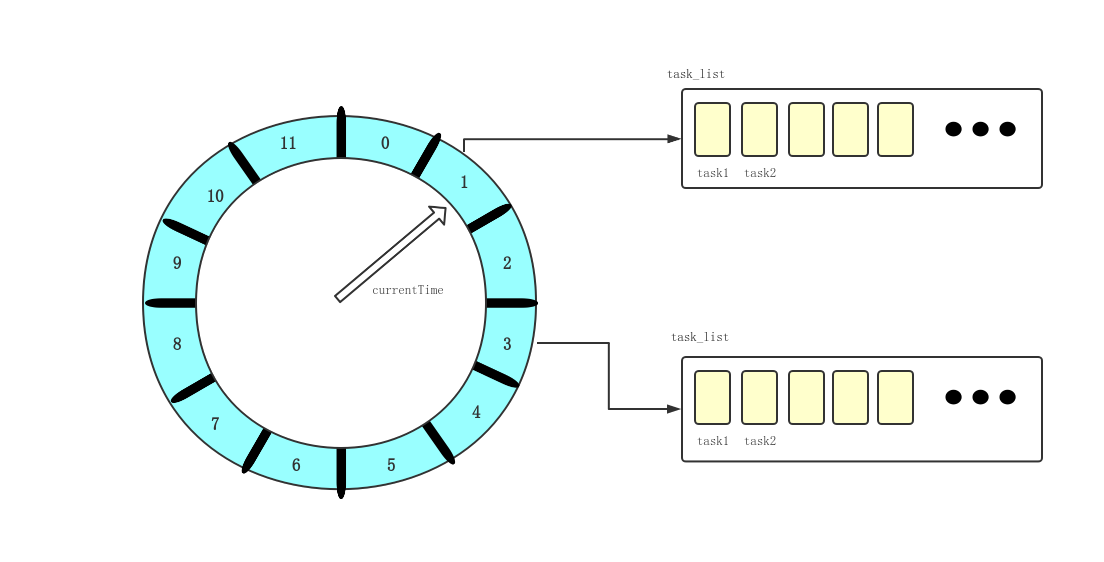
这里先对时间轮的一些概念进行定义：

• tickMs：基本时间跨度。时间轮由多个时间格组成，每个时间格代表当前时间轮的基本时间跨度。
• wheelSize：时间格个数。一个时间轮完成定义后，其时间格的个数是固定的。
• interval：时间跨度。一个时间轮的总体时间跨度 interval = tickMs * wheelSize。
• currentTime：当前时间。相当于时间轮的表盘指针，表示当前所处的时间，其取值通常是 tickMs 的整数倍。已经被指向的时间格属于到期部分，其对应的任务队列都需要被取出执行。

随着时间的不断推移，指针 currentTime 的位置不断向前推进。当有一个新的定时任务进来时，则在当前 currentTime 位置的基础上，加上对应的相对时间，则为新任务应该插入的队列位置。

简单时间轮算法

任务队列在加入时间轮时已经按照其执行时间完成了有序的归位，因此当轮询线程遍历到某一个时间格时，当前时间格对应的任务队列中的所有任务就可以开始直接执行，不需要再检查任务执行的时间戳是否已达到。

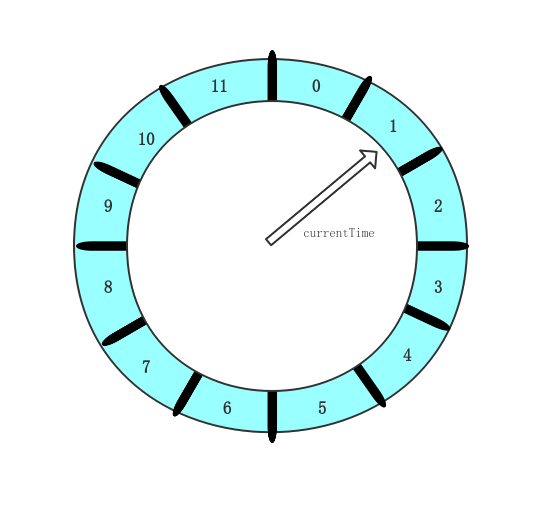
类比钟表表盘的形象，我们的时间轮可以以小时为粒度，每个时间格代表一个小时，但在实际应用中，定时任务的调度常常精确到分钟或者秒钟的粒度。如果一个定时任务需要指定在每天的某一个时刻执行，精确到秒，那么时间轮则需要支持一天 24 * 60 * 60 = 86400 个刻度。其占用的内存空间很大，但实际任务占用的可能只有几个甚至几十个，严重浪费系统资源。

round 的时间轮算法

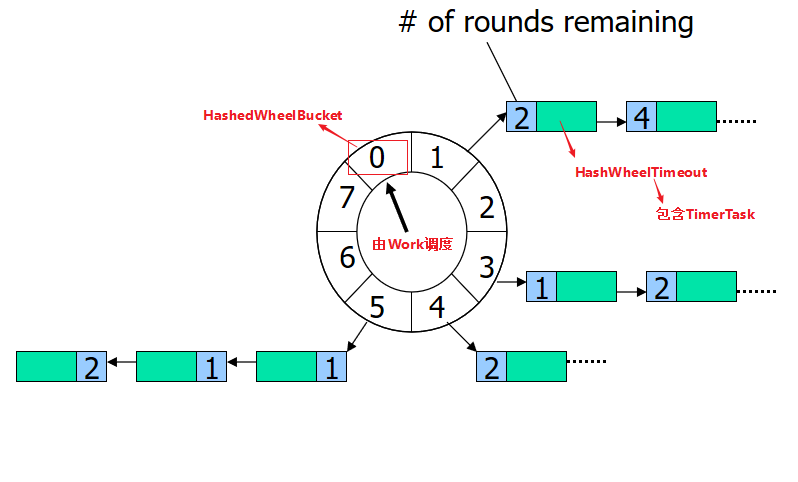
为了处理上面提到的问题，我们可以在每个定时任务中增设一个 round 字段，用以标识当前任务还需要在时间轮中遍历几轮，才进入执行的时间判断轮。其执行逻辑为：每次遍历到一个时间格后，其任务队列上的所有任务 round 字段减 1，如果 round 字段变为 0，则将任务移出队列，提交给异步线程池来执行其内容。如果这是一个重复任务，那么提交后再将它重新添加到任务队列中。

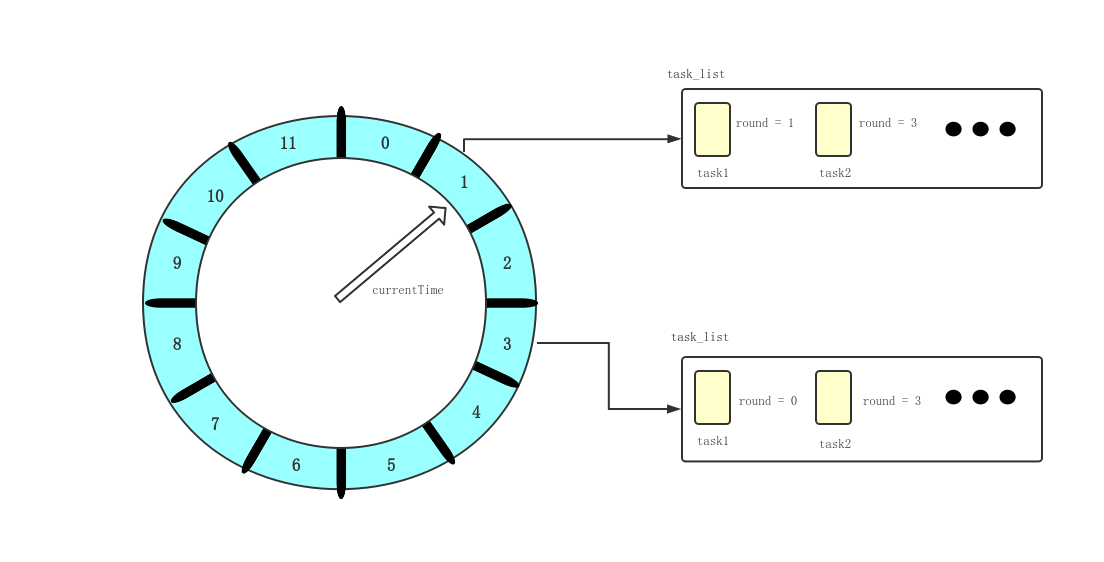
假设现在将时间轮的精度设置为秒，时间轮共有 60 个时间格，那么一个 130 秒后执行的任务，可以将其 round 字段设为 2，并将任务加入到时间刻度为 10 的任务队列中。即对于间隔时间为 x 的定时任务：

• round = x / 60 （整除）
• 刻度位置 pos = x % 60

这种方式虽然减少了时间轮的刻度个数，但并没有减少轮询线程的轮询次数，其效率还是相对比较低。时间轮每遍历一个时间刻度，就要完成一次判断和执行的操作，其运行效率与一般的任务队列差别不大，并没有太大的效率提升。完成了一次遍历，但是并没有提交可执行的任务，这种现象可以称之为“空轮询”。

分层时间轮算法

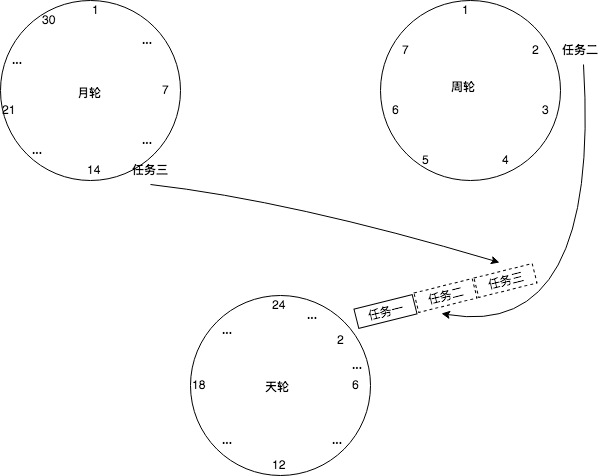
另一种对简单时间轮算法改良的方案，可以参照钟表中时、分、秒的设计，设置三个级别的时间轮，分别代表时、分、秒，且每个轮分别带有 24、60、60 个刻度。这样子三个时间轮结合使用，就能表达一天内所有的时间刻度了。

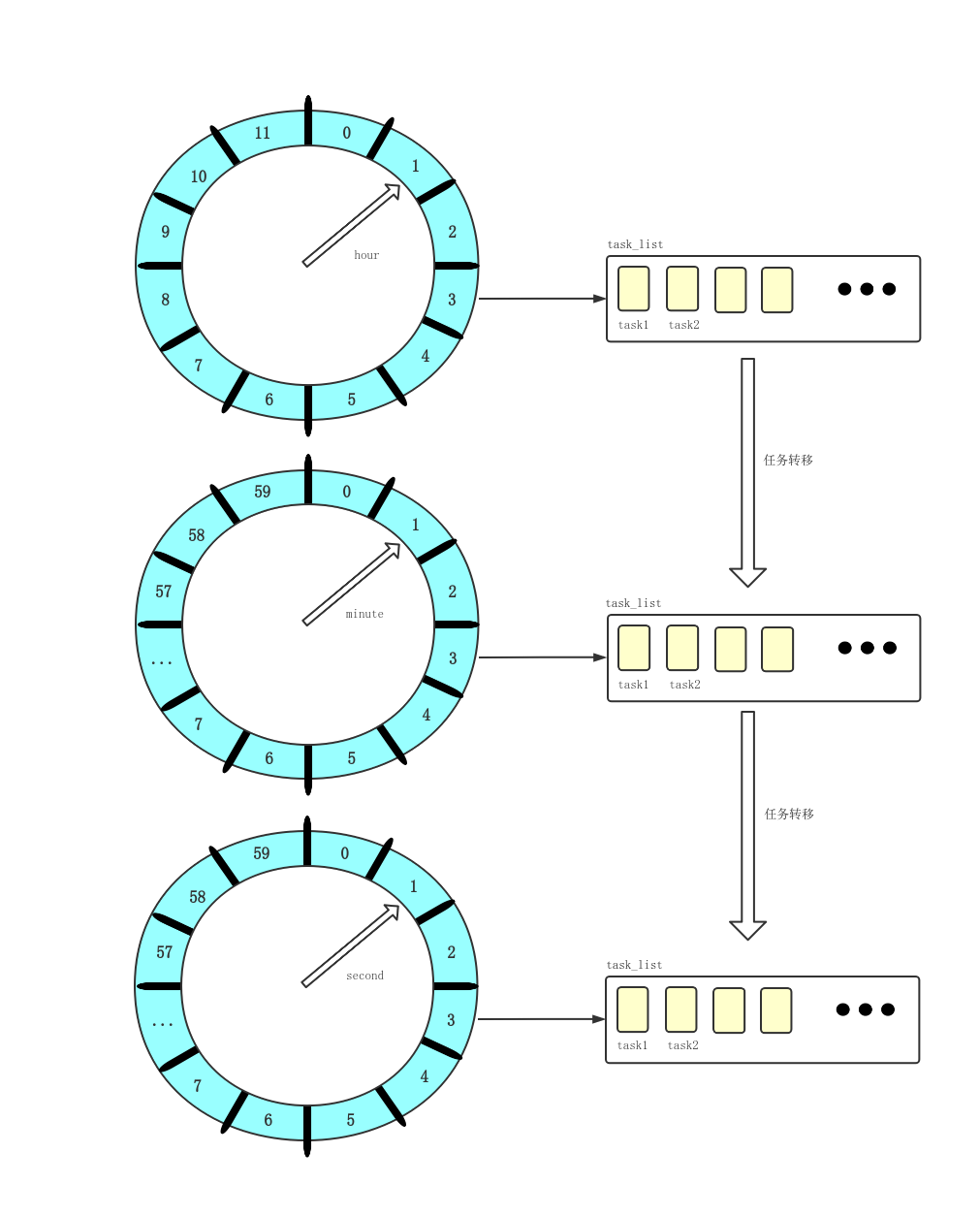
当 hour 时间轮的轮询线程轮询到执行的时间格时，其对应的任务队列已达到其执行的 hour 时间。此时这些任务需转移到下一层 minute 时间轮中，根据其执行时间的 minute 位，插入到对应的任务队列中。后续的步骤都类似，直至到最后一层 second 的时间轮中，被轮询到的队列即可提交其所有的任务到异步执行线程池中。

采用分层时间轮的方式，不需要引入 round 字段，只要在最后一级遍历到的任务队列，必然是可提交执行的，进而避免了空轮询的问题，提高了轮询的效率。每个时间轮的遍历由不同的轮询线程实现，虽然引入的线程并发，但是线程数仅仅跟时间轮的级数有关，并不会随着任务数量的增加的增加。

时间轮算法的进一步优化

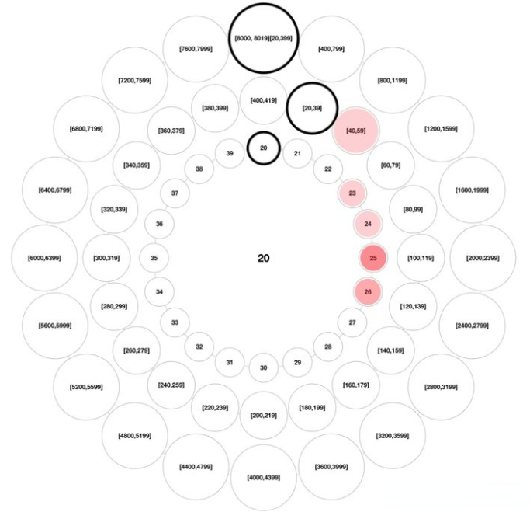
通过分层时间轮，我们可以将一系列定时任务根据其执行时间进行分组和排序，依次分配到时间轮的对应时间格中。只要时间轮的指针到达特定时间格，相应任务队列中的所有任务即可提交执行。但是在实际应用中，真正需要执行任务的时间格在所有时间格中的占比是很小的。假如第一个待执行的任务列表的 expiration 为 100s，以每秒推进一格的方案来看，在获取到第一个可执行的任务列表前，会出现 99 次的空轮询，也就是时间轮指针推进了，但并没有任务执行的情况。这种空轮询的存在，并没有太大的业务含义，白白耗费了系统的性能资源。

为了处理好空轮询的问题，这里可以再引入 DelayQueue 来维护每个定时任务列表，进而减少空轮询的次数，实现精确轮询。具体方案就是，根据 DelayQueue 中前后相邻的任务队列的 expiration 来确定时间轮指针推进的时间，精确地在下一个任务执行的时间点时对该列表进行轮询。

性能分析

一个初级的定时任务框架，可以采用有序任务队列 + 轮询线程的方式进行实现，有序任务队列通常基于优先队列（堆）进行实现，因此其任务的插入和删除的时间复杂度为 O(log N) 。而时间轮算法，能够将时间复杂度降低至 O(1)，效率明显得到提升。而算法的主要性能损耗，则体现在多个时间轮轮询线程的时间推进，以及他们与任务执行线程之间的切换。这方面的复杂度，明显小于基本的时间轮算法还有普通的任务队列。

定义：

• n - 任务数量
• k - 多线程轮询的线程数
• 常数 M - 全时段时间轮刻度数量（空间单位数）
• 常数 L - 单 round 时间轮刻度数量（空间单位数）
• $l_i$ - 第 i 层时间轮刻度数量（空间单位数）
• T - 存在任务队列的空间单位数

模型	插入复杂度	删除复杂度	轮询复杂度	空间复杂度
普通双向链表	O(1)	O(n)	O(n)	O(n)
有序双向链表	O(n)	O(n)	O(n)	O(n)
k 个分组的有序双向链表	O(n)	O(n)	O(n / k) ; CPU的系统调度	O(n)
简单时间轮	O(1)	O(1)	M	M
round 时间轮	O(1)	O(1)	M	L
分层时间轮	O(1)	O(1)	$\Sigma l_i$	$\Sigma l_i$
分层时间轮 + 延时队列	O(1)	O(1)	T ( <= $\Sigma l_i$ )	$\Sigma l_i$

实现 demo 可以参考资源：https://download.csdn.net/download/sinat_36645384/86800184