关于中国邮递员问题和欧拉图应用

 

中国邮递员问题：

1962年有管梅谷先生提出中国邮递员问题（简称CPP）。一个邮递员从邮局出发，要走完他所管辖的每一条街道，可重复走一条街道，然后返回邮局。任何选择一条尽可能短的路线。

这个问题可以转化为：给定一个具有非负权的赋权图G，

（1）用添加重复边的方法求G的一个Euler赋权母图G*，使得尽可能小。

（2）求G*的Euler 环游。

人们也开始关注另一类似问题，旅行商问题（简称TSP）。TSP是点路优化问题，它是NPC的。而CPP是弧路优化问题，该问题有几种变形，与加权图奇点的最小完全匹配或网络流等价，有多项式算法。[1]

 

欧拉图：

图G中经过每条边一次并且仅一次的回路称作欧拉回路。存在欧拉回路的图称为欧拉图。

 

无向图欧拉图判定：

       无向图G为欧拉图，当且仅当G为连通图且所有顶点的度为偶数。

 

有向图欧拉图判定：

       有向图G为欧拉图，当且仅当G的基图[2]连通，且所有顶点的入度等于出度。

 

欧拉回路性质：

性质1　设C是欧拉图G中的一个简单回路，将C中的边从图G中删去得到一个新的图G’，则G’的每一个极大连通子图都有一条欧拉回路。

性质2　设C1、C2是图G的两个没有公共边，但有至少一个公共顶点的简单回路，我们可以将它们合并成一个新的简单回路C’。

 

欧拉回路算法：

1             在图G中任意找一个回路C；

2             将图G中属于回路C的边删除；

3             在残留图的各极大连通子图中分别寻找欧拉回路；

4             将各极大连通子图的欧拉回路合并到C中得到图G的欧拉回路。

由于该算法执行过程中每条边最多访问两次，因此该算法的时间复杂度为O(|E|)。

如果使用递归形式，得注意|E|的问题。使用非递归形式防止栈溢出。

如果图 是有向图，我们仍然可以使用以上算法。

http://acm.hdu.edu.cn/showproblem.php?pid=1116  有向图欧拉图和半欧拉图判定

http://acm.pku.edu.cn/JudgeOnline/problem?id=2337 输出路径

 

中国邮递员问题①：

一个邮递员从邮局出发，要走完他所管辖的每一条街道，可重复走一条街道，然后返回邮局。所有街道都是双向通行的，且每条街道都有一个长度值。任何选择一条尽可能短的路线。

       分析：

              双向连通，即给定无向图G。

              如果G不连通，则无解。

              如果G是欧拉图，则显然欧拉回路就是最优路线。

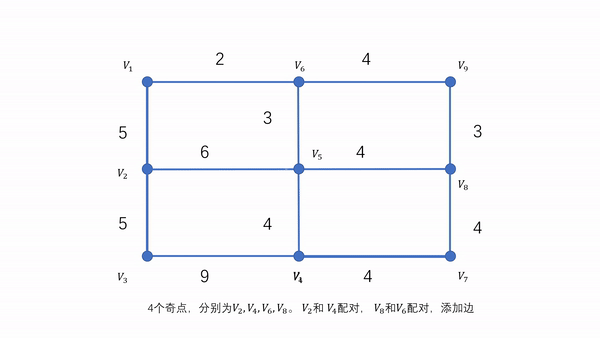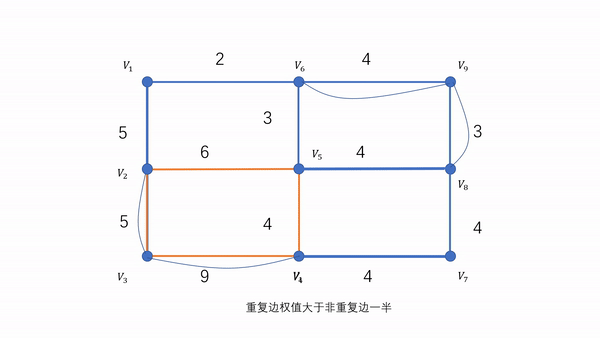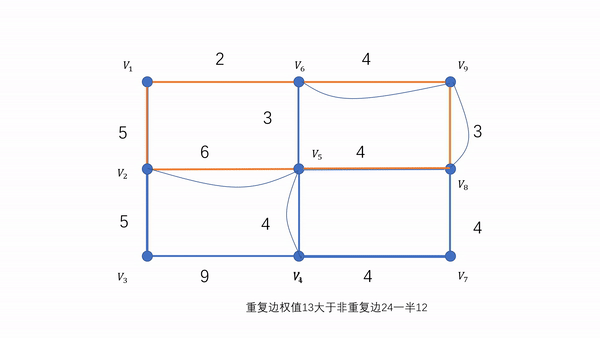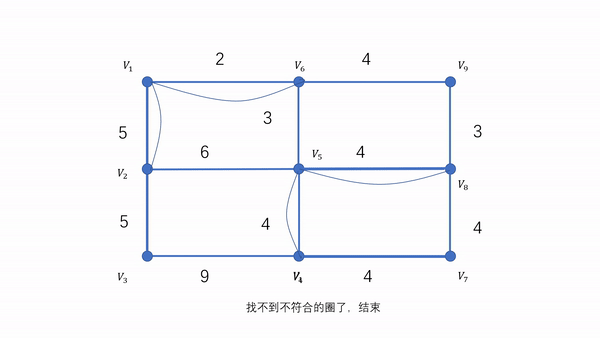
              如果G连通，但不是欧拉图，说明图中有奇点[3]。奇点都是成对出现的，证明从略。

对于最简单情况，即2个奇点，设（u，v）。我们可以在G中对（u，v）求最短路径R，构造出新图G’ = G ∪ R。此时G’就是欧拉图。

证明：u和v加上了一条边，度加一，改变了奇偶性。而R中其他点度加二，奇偶性不变。

由此可知，加一次R，能够减少两个奇点。推广到k个奇点的情况，加k/2个R就能使度全为偶数。

 

接下的问题是求一个k个奇点的配对方案，使得k/2个路径总长度最小。

这个就是无向完全图最小权匹配问题。有一种Edmonds算法，时间复杂度O（N^3）。[4]

也可转换为二分图，用松弛优化的KM算法，时间复杂度也是O（N^3）。

             

              完整的算法流程如下：

1         如果G是连通图，转2，否则返回无解并结束；

2         检查G中的奇点，构成图H的顶点集；

3         求出G中每对奇点之间的最短路径长度，作为图H对应顶点间的边权；

4         对H进行最小权匹配；

5         把最小权匹配里的每一条匹配边代表的路径，加入到图G中得到图G’；

6         在G’中求欧拉回路，即所求的最优路线。

 

中国邮递员问题②：

和①相似，只是所有街道都是单向通行的。

分析：

       单向连通，即给定有向图G。

       和①的分析一样，我们来讨论如何从G转换为欧拉图G’。

首先计算每个顶点v的入度与出度之差 d’（v）。如果G中所有的v都有d’（v）=0，那么G中已经存在欧拉回路。

d’（v）>0 说明得加上出度。d’（v）<0说明得加上入度。

而当d’（v）=0，则不能做任何新增路径的端点。

可以看出这个模型很像网络流模型。

顶点d’（v）>0对应于网络流模型中的源点，它发出d’（v）个单位的流；顶点d’（v）<0对应于网络流模型中的汇点，它接收-d’（v）个单位的流；而d’（v）=0的顶点，则对应于网络流模型中的中间结点，它接收的流量等于发出的流量。在原问题中还要求增加的路径总长度最小，我们可以给网络中每条边的费用值 设为图 中对应边的长度。这样，在网络中求最小费用最大流，即可使总费用最小。

 

这样构造网络N：

1         其顶点集为图G的所有顶点，以及附加的超级源 和超级汇 ；

2         对于图G中每一条边(u,v)，在N中连边(u,v)，容量为∞，费用为该边的长度；

3         从源点 向所有d’(v)>0的顶点v连边(s,v)，容量为d’(v)，费用为0；

4         从所有d’(v)<0的顶点 向汇点t连边(u,t)，容量为-d’(v)，费用为0。

 

　　       完整的算法流程如下：

1         如果G的基图连通且所有顶点的入、出度均不为0，转2，否则返回无解并结束；

2         计算所有顶点v的d’(v)值；

3         构造网络N；

4         在网络N中求最小费用最大流；

5         对N中每一条流量f(u,v)的边(u,v)，在图G中增加f(u,v)次得到G’；

6         在G’中求欧拉回路，即为所求的最优路线。

 

      NPC问题：

如果部分街道能够双向通行，部分街道只能单向通行。这个问题已被证明是NPC的。[5]