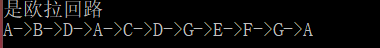中国邮递员问题的求解实例
前面已经讲过,对于欧拉图,可以直接用Fleury算法找出一条欧拉巡回路线;对于半欧拉图,可以先求出奇点u和v之间的最短路径P,令G =G P,贝U G *为欧拉图,然后用Fleury算法来确定一个G *的欧拉巡回,它就是G的最优巡回。
当G有2n个奇点(n>1),可以用Edmonds算法解决,步骤如下:
(1) 用Floyd算法求出所有奇点之间的最短路径和距离矩阵。
(2) 用匈牙利法或0-1规划法求出所有奇点之间的最佳配对。
(3) 在原图上添加最佳配对所包含的两两顶点之间的最短路得到欧拉图G *。
⑷用Fleury算法确定一个G *的欧拉巡回,这就是G的最优巡回。
以上步骤的关键是找出2n个奇点的最佳配对,举例如下。
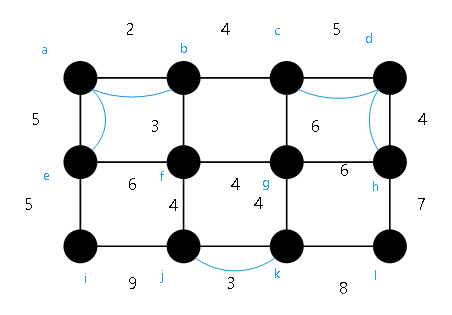
例图3是某区街道示意图,各边的长度数据如下表所示。现在需要对每条街道
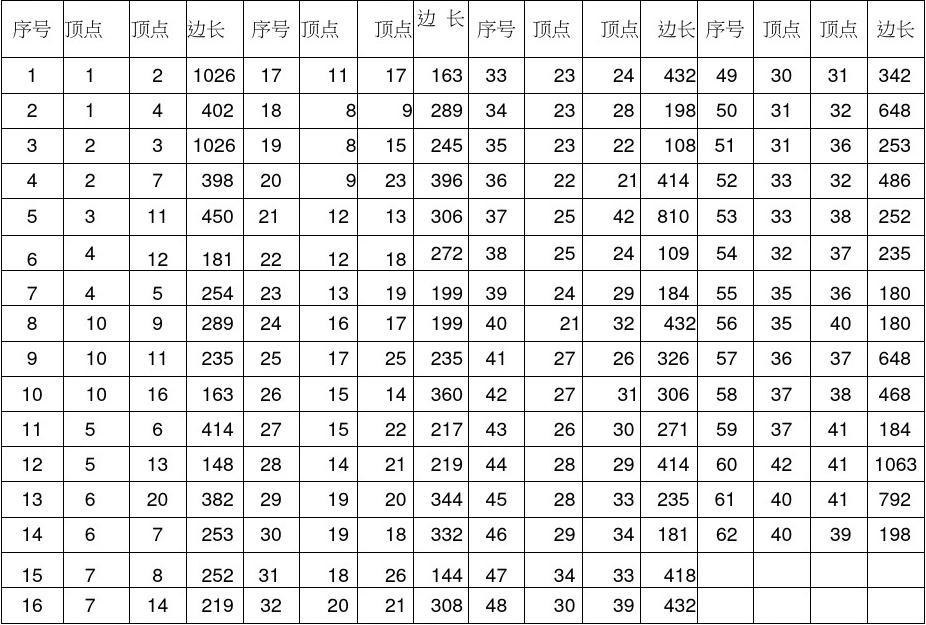
找最优巡回,需要先求26个奇点的最佳配对。
先用Floyd算法求出所有42个顶点之间的最短路距离和路径。程序如下:
E=[1 2 1026
1 4 402
........ 注:每一行代表一条边(两个顶点和边长),此处省略59行
40 39 198];
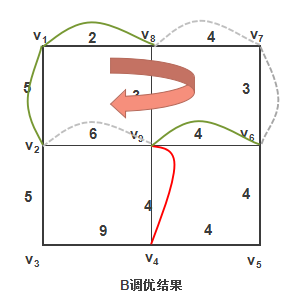




![[算法导论] 邮递员问题](https://img-blog.csdnimg.cn/2021042111073135.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1RyYW5jZTk1,size_16,color_FFFFFF,t_70)