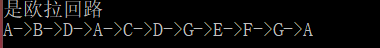问题描述

代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>#define min(a,b) ( (a) < (b) ? (a) : (b) )
#define MAX_NODE 100
#define MAX_EDGE 100
#define INF 0x7fffffff      // 表示两点不连通typedef struct 
{int number;   // 标记位int cost;     // 结点间距int dis;      // 结点最近距离
}Node;typedef struct 
{int from;     // 边起点int to;       // 边终点int dis;      // 边距离
}Edge;int n, m;                              // 点的个数和边的个数
int total_edge, odd_point;             // 总边数和奇点数
Node map[MAX_NODE][MAX_NODE];          // 结点连接情况
int point[MAX_NODE];                   // 每个结点的度数
int need_add_num, min_count, edge_num; // 需要添加边的个数  
Edge odd_edge[MAX_EDGE];
int point_flag[MAX_EDGE];
int min_edge[MAX_EDGE];
int tmp_edge[MAX_EDGE];
int top;
int finish_flag = 0;
int path_stack[MAX_EDGE];void Floyd()
{// 比较i到j直达近还是从i到k加上k到j近。添加的结点k放在最外层循环。for (int k = 1; k <= n; k++)for (int i = 1; i <= n; i++)if(map[i][k].dis != INF){for (int j = 1; j < n; j++)if(map[k][j].dis != INF){map[i][j].dis = map[j][i].dis = min(map[i][j].dis, map[i][k].dis + map[k][j].dis);}}
}void search_edge(int count, int step)
{// 深度还是广度遍历寻找最优方案// step用于记录数量，count记录最短长度// 寻找路径存入了数组中，可通过i访问if (step == need_add_num){if (count < min_count){for (int i = 0; i < need_add_num; i++){min_edge[i] = tmp_edge[i];}min_count = count;}return;}int a, b, c;for (int i = 0; i < edge_num; i++){a = odd_edge[i].from;b = odd_edge[i].to;c = odd_edge[i].dis;if (point_flag[a] == 1 && point_flag[b] == 1)// 如果两点均未相连{point_flag[a] = point_flag[b] = 0;    // 置标记位为0tmp_edge[step] = i;search_edge(count + c, step + 1);point_flag[a] = point_flag[b] = 1;}}
}void dijkstra_to_add_edge(int s, int e)
{int dis[MAX_NODE];       // 点到起始（s）点的距离int used[MAX_NODE];      // 标记位int pre[MAX_NODE];       // 记录其从哪一点过来的，方便回溯memset(used, 0, sizeof(used));   // 初始化一波for (int i = 1; i <= n; i++){dis[i] = INF;}dis[s] = 0;while (1){int v = -1;for (int i = 1; i <= n; i++){if (!used[i] && (v == -1 || dis[i] < dis[v])){v = i;}}if (v == e || v == -1)// 当当前点是末点e时或本身v就是最小时break;used[v] = 1;    // 修改标记位for (int i = 1; i <= n; i++){if (map[v][i].cost < INF && (dis[v] + map[v][i].cost) < dis[i]){pre[i] = v;dis[i] = dis[v] + map[v][i].cost;}}}int v = e;int pre_node = e;while (pre_node != s){pre_node = pre[v];++map[pre_node][v].number;    // 加边++map[v][pre_node].number;}
}void extend_edge(int add_num)
{need_add_num = add_num;memset(point_flag, 0, sizeof(point_flag));edge_num = 0;// 当两个点都是奇点的时候for (int i = 1; i < n; i++){if ((point[i] & 0x1) == 1){for (int j = i+1; j <= n; j++){if ((point[j] & 0x1) == 1 && map[i][j].dis < INF){point_flag[i] = point_flag[j] = 1;   // 将i，j两点标记为需要被连接的奇点odd_edge[edge_num].from = i;         // 将相关信息存入odd_edge数组中odd_edge[edge_num].to = j;odd_edge[edge_num].dis = map[i][j].dis;edge_num++;}}}}min_count = INF;    // 设置最小值，方便比较search_edge(0, 0);if (min_count < INF){int a, b;for (int i = 0; i < need_add_num; i++){int k = min_edge[i];a = odd_edge[k].from;b = odd_edge[k].to;dijkstra_to_add_edge(a, b);   // 用dijkstra算法求加边后两点最短距离point[a] = point[b] = 0;}odd_point -= add_num * 2;total_edge += add_num;}else{exit(-1);}}void search_euler_path(int s)
{for (int i = 1; i <= n; i++){if (map[s][i].number > 0){--map[s][i].number;--map[i][s].number;path_stack[top++] = i;if (top == (total_edge + 1))// 结点比总边数多1{finish_flag = 1;return;}search_euler_path(i);if (finish_flag)return;++map[s][i].number;++map[i][s].number;--top;}}
}int main()
{FILE *stream = freopen("E:\\0_Re5et\\数据结构\\考试\\邮递员\\a1.in", "r", stdin);if (stream == NULL){exit(1);}while (scanf("%d %d", &n, &m) != EOF){// 初始化memset(point, 0, sizeof(point));for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)map[i][j].cost = map[i][j].dis = INF;total_edge = 0;// 读入图的数据int a, b, c;for (int i = 0; i < m; i++){scanf("%d %d %d", &a, &b, &c);map[a][b].cost = map[b][a].cost = c;map[a][b].dis = map[b][a].dis = c;map[a][b].number = map[b][a].number = 1;++point[a];++point[b];++total_edge;}odd_point = 0;for (int i = 1; i <= n; i++)// 判断点是否为奇点{if ((point[i] & 0x1) == 1){odd_point++;}}int first_id = 1;    // 设置邮局的位置 1即为Aif (odd_point > 2)// 奇点个数大于两个的时候，用floyd算法更新任意两点之间最短路径，并且添加边{Floyd();extend_edge(odd_point / 2);// 两个奇点添加一条边，共需要添加odd_point/2条边}top = 0;if (odd_point == 2)// 奇点个数为2的时候，从一个奇点出发到另一个奇点去，但不能构成环路，直接退出程序{for (int i = 1; i <= n; i++){if ((point[i] & 0x1) == 1){first_id = i;break;}}if (first_id != 1){exit(-2);}}path_stack[top++] = first_id;// 利用栈进行深度搜索来确定最短路线并存入数组search_euler_path(first_id);char vex;// 将最短路线输出for (int i = 0; i <= total_edge; i++){vex = path_stack[i] + 'A' - 1;printf("%c", vex);if (i < total_edge){printf("->");}}printf("\n");}return 0;
}

说明

问题描述如下：邮递员从邮局（★）出发走遍每条街道，最后返回邮局，邮递员应按怎样的顺序投递，才能使经过的路径长度最小。本题的原型是著名的“一笔画”问题。根据图论 的定理可知，任何一个图若要能一笔画成，则必须同时满足以下两个条件，其一：该图是连通的；其二：图中度数为奇数的点（又称为奇度点）的个数为不多于两个。
在图中，共有A、C、E、F、G、H、J、L等8个奇度点，因此该图不一笔画成，即邮递员从邮局出发，要想走遍所有街道，某些街道必定会重复经过。因此，此问题的关键在于如何向图中“添加”若干条代价最小的边，使得此图最终满足一笔画的条件。要解决此问题，即可转换为以下两个具体问题：
其一：“添加”哪些边？
显然，“添加”的边所依附的顶点必须均是奇度点。图中有8个奇度点，我们可以组合成4条边，这样使得奇度点的个数为0个。
其二：如何选择代价最小的边？
因为图中8个奇度顶点组合成4条边的情形有很多种，所以要分别求出每种组合形成的边的代价，然后从中选出代价最小的边。
另外，在此问题中，边的“添加”的应该理解为从一个奇度点到另一个奇度点之间的路径。
“邮递员”问题的算法描述如下:
（1） 建立街区无向网的邻接矩阵；
（2） 求各顶点的度数；
（3） 求出所有奇度点；
（4） 求出每一个奇度点到其它奇度点的最短路径；
（5） 找出距离最短的添加方案；
（6） 根据最佳方案添加边，对图进行修改，使之满足一笔画的条件；
（7） 对图进行一笔画，并输出；

实验总结

程序首先读入文件，读取结点个数和边条数以及点与点间的连通关系，并建立街区无向网的邻接矩阵，同时记录各结点度数。
随后遍历各结点，找出其中所有的奇点。如果奇点个数大于2，则需要加边来使奇点数为0；如果奇点正好为两个，则从其中一个点出发，到另一点结束能形成欧拉图，但是不能形成回路，也不能保证从邮局出发；如果奇点数为0，则可以形成欧拉回路。接下来分情况讨论：
当奇点数大于2的时候：通过Floyd算法求任意两点路径的最短距离，并将读入的图的数据更新为最短路径。随后进入extend_edge()函数。通过标记的方法来加边。当某一边的始点与终点均为奇点，并且两点间可连通时，将需要加边的始点和终点以及距离信息存入odd_edge中。随后通过一个深度遍历，判断需要加的边是否为最短的，即确定距离最短的添加方案。随后用dijkstra算法确定从该始点到终点的最短路径。
当奇点数等于2的时候，判断起始点能否为1，若可以，则设置first_id = 1即可。若不能，则无法构成环路。
用数组实现一个栈的功能，将行走路径经历的结点添加到栈中，每走过一条边，number个数就减一，栈中结点数就加一，当栈中元素的个数达到总边数加一时，结束递归，这时栈中存放了一笔画最短路径。将其输出即可。