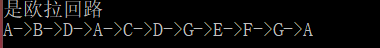邮递员算法问题之c++实现

article/2025/10/8 7:29:09

在这里插入图片描述

前言

大家好，我是Ericam_。
近些时间，通过一个项目接触到了邮递员算法问题，还是挺有意思的（虽然做起来经历了不少的困难）。最后勉强复现了吧，写个文章就当记录一下。

演示

在这里插入图片描述

问题介绍

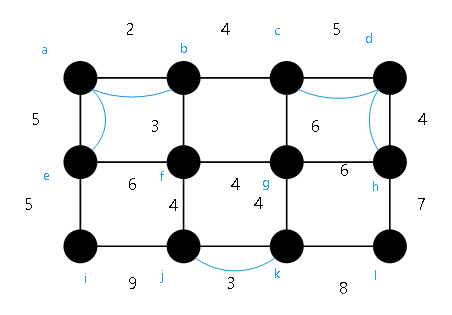
1962年有管梅谷先生提出中国邮递员问题（简称CPP）。一个邮递员从邮局出发，要走完他所管辖的每一条街道，可重复走一条街道，然后返回邮局。任何选择一条尽可能短的路线。

当邮递员可以每条道路仅走一次便返回起点，那该路线一定是最短的。而欧拉回路恰巧满足这种条件。那什么才是欧拉回图呢？

什么是欧拉回图？

欧拉回图：每个点的入度和出度必须相等（起始点也一样），也就是说，每个节点的度应该是偶数个。

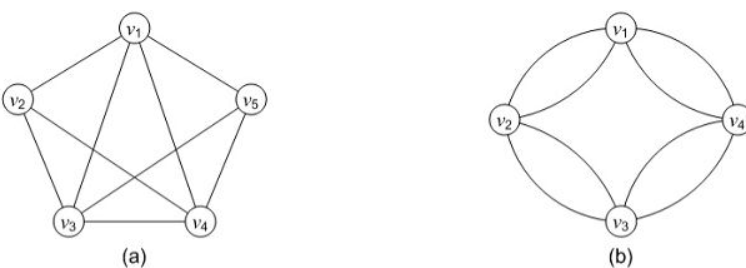
在这里插入图片描述
但在实际生活中，基本上这种特殊情况是不存在的，所以我们想要解决邮递员问题，首要便是要构造欧拉回图，只要能够花费最小的代价来构造欧拉回图，那么邮递员问题便得到解决了。

所以首先我们要找到图中所有的奇度点，（奇度点个数一定是偶数个，这里就不证明了），当奇度点两两相连后，找到耗费最少的一组组合即可。

思路

以下给出我个人的思路，如有疏漏，请多包涵🤭~

首先我们需要找到图中所有的奇度点
接下来我们需要比较路径长度。由于图一定是连通图，所以每两个点之间都会存在直接或间接的路径，但两个点之间可能存在多条路径，所以我们需要先求出点与点之间的最短路径。由于是多源最短路径求解，所以需要使用Floyd算法来解决问题。
接下来将奇度点两两分组，计算路径长度，然后挑选耗费最少的一个分组。
构建欧拉回图，解决问题~

代码复现

由于其他原因，不会公开源代码。但可以分享关键操作~

1.首先如何计算出奇度点？

'''
遍历邻接矩阵，挑选出度数为奇数的点即可。用vector来存放顶点序号。
'''

2.Floyd最短路径求解

常规的Floyd算法求解，利用path来存放中介点，方便回溯路径。

//Floyd最短路径计算函数
void MGraph::Floyd(){//更新disfor(int i=0;i<this->n;i++)for(int j=0;j<this->n;j++)if(this->edges[i][j]!=-1){this->dis[i][j] = this->edges[i][j];this->path[i][j] = -1;}for(int k=0;k<this->n;k++)for(int i=0;i<this->n;i++)for(int j=0;j<this->n;j++)if(this->dis[i][k]+this->dis[k][j]<this->dis[i][j]){this->dis[i][j] = this->dis[i][k]+this->dis[k][j];this->path[i][j] = k;}
}

3 . 通过DFS来分组，寻找耗费最小的组合。（难点）

这里是我觉得最难的一点，同样我的方法也不够好。之后想过很多改进，但甚至不如原方法…
个人思路：

利用vector v来存放点，每次挑选两个点作为一组存入，当v中点个数等于奇度点个数时，一个组合便完成了，计算v中每个组的两个点的路径长度并求和，然后判断是否最小。

//组合(输出所有奇数点的排列组合)
void MGraph::DFS(vector<int>v){//组合完成if(v.size()==this->odd_vex.size()){float sum=0.0;for(int i=0;i<v.size();i+=2){sum += this->dis[v[i]][v[i+1]];}if(sum<this->min_addDis){this->mindis_oddvex = v;this->min_addDis = sum;}return;}for(int i=0;i<this->odd_vex.size()-1;i++){//如果v中已存在节点iif(this->exists(v,this->odd_vex[i]))continue;for(int j=i+1;j<this->odd_vex.size();j++){//如果v中已存在节点jif(this->exists(v,this->odd_vex[j]))continue;vector<int>new_v(v);new_v.push_back(this->odd_vex[i]);new_v.push_back(this->odd_vex[j]);this->DFS(new_v);}}
}

4 .求邮递员行走路线

这里就如同迷宫问题一样，往前走即可，走过去便删除走过的边（某些边可能存在多条）。

//求欧拉路径
void MGraph::getEulerpath(int v){for(int i=0;i<this->n;i++){if(this->edges_num[v][i]>0){this->edges_num[v][i]--;this->edges_num[i][v]--;this->euler_path.push(i);//当欧拉路径中顶点个数等于图总边数+1(因为返回起点)，寻找完成if(this->euler_path.size() == this->e+1){this->finish_eulerpath = 1;return;}getEulerpath(i);if(this->finish_eulerpath)return;this->euler_path.pop();this->edges_num[v][i]++;this->edges_num[i][v]++;}}
}