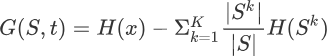观察两个事件同时发生时获得的信息量应该等于观察到事件各自发生时获得的信息之和?
两个事件的信息量之和等于两个事件和的信息量?
两个随机变量熵的和大于两个随机变量和的熵

图片引自:https://blog.csdn.net/luoxuexiong/article/details/113059152#:~:text=%E5%9C%A8%E6%A6%82%E7%8E%87%E8%AE%BA%E5%92%8C%E4%BF%A1%E6%81%AF%E8%AE%BA%E4%B8%AD%EF%BC%8C%E4%B8%A4%E4%B8%AA%E9%9A%8F%E6%9C%BA%E5%8F%98%E9%87%8F%E7%9A%84%E4%BA%92%E4%BF%A1%E6%81%AF%EF%BC%88Mutual%20Information%EF%BC%8C%E7%AE%80%E7%A7%B0MI%EF%BC%89%E6%88%96%E8%BD%AC%E7%A7%BB%E4%BF%A1%E6%81%AF%EF%BC%88transinformation%EF%BC%89%E6%98%AF%E5%8F%98%E9%87%8F%E9%97%B4%E7%9B%B8%E4%BA%92%E4%BE%9D%E8%B5%96%E6%80%A7%E7%9A%84%E9%87%8F%E5%BA%A6%E3%80%82.%20%E4%B8%8D%E5%90%8C%E4%BA%8E%E7%9B%B8%E5%85%B3%E7%B3%BB%E6%95%B0%EF%BC%8C%E4%BA%92%E4%BF%A1%E6%81%AF%E5%B9%B6%E4%B8%8D%E5%B1%80%E9%99%90%E4%BA%8E%E5%AE%9E%E5%80%BC%E9%9A%8F%E6%9C%BA%E5%8F%98%E9%87%8F%EF%BC%8C%E5%AE%83%E6%9B%B4%E5%8A%A0%E4%B8%80%E8%88%AC%E4%B8%94%E5%86%B3%E5%AE%9A%E7%9D%80%E8%81%94%E5%90%88%E5%88%86%E5%B8%83%20p%20%28X%2CY%29%20%E5%92%8C%E5%88%86%E8%A7%A3%E7%9A%84%E8%BE%B9%E7%BC%98%E5%88%86%E5%B8%83%E7%9A%84%E4%B9%98%E7%A7%AF%20p%20%28X%29p,%E7%9A%84%E7%9B%B8%E4%BC%BC%E7%A8%8B%E5%BA%A6%E3%80%82.%20%E4%BA%92%E4%BF%A1%E6%81%AF%20%28Mutual%20Information%29%E6%98%AF%E5%BA%A6%E9%87%8F%E4%B8%A4%E4%B8%AA%E4%BA%8B%E4%BB%B6%E9%9B%86%E5%90%88%E4%B9%8B%E9%97%B4%E7%9A%84%E7%9B%B8%E5%85%B3%E6%80%A7%20%28mutual%20dependence%29%E3%80%82.%20%E4%BA%92%E4%BF%A1%E6%81%AF%E6%98%AF%E7%82%B9%E9%97%B4%E4%BA%92%E4%BF%A1%E6%81%AF%EF%BC%88PMI%EF%BC%89%E7%9A%84%E6%9C%9F%E6%9C%9B%E5%80%BC%E3%80%82.%20%E4%BA%92%E4%BF%A1%E6%81%AF%E6%9C%80%E5%B8%B8%E7%94%A8%E7%9A%84%E5%8D%95%E4%BD%8D%E6%98%AFbit%E3%80%82.

1.自信息 (self-information)
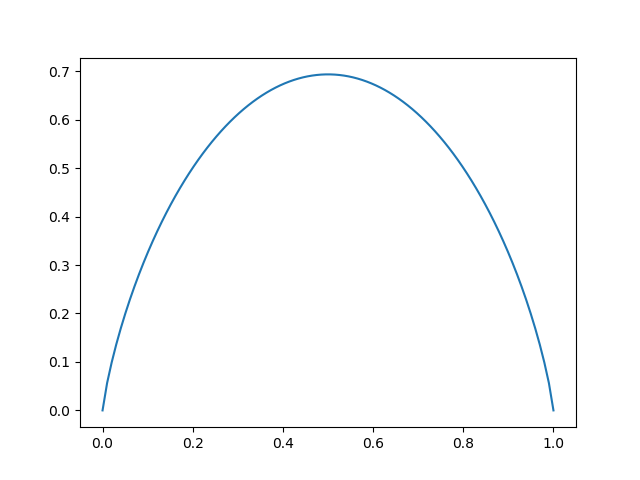
I(x)=− log p(x)
自信息表示子事件的信息量 (概率越小,信息量越大)
如果事件X=x的概率为p ,那么X可以视作由1/p个这样的事件构成,需要长度为log(1/p)的编码对这1/p个事件进行编码

图片来源:https://www.cnblogs.com/kyrieng/p/8694705.html
2.信息熵 (Shannon’s entropy)
信息熵:随机变量中所有事件的平均信息量,即自信息的期望
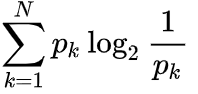
min H=0
max H=ln n ,离散对象
max H=ln l ,连续对象
log 函数基的选择是任意的
信息论中基常常选择为2,因此信息的单位为比特bits;
机器学习中基常常选择为自然常数,因此单位常常被称为奈特nats
An attribute with a very large domain normally divides the database into more smaller classes than an attribute with a small domain. A regularity found in a very small portion of database may not necessarily be useful. On the other hand, an attribute with small domain usually divides the database into a few larger classes. One may not find regularities in such large subsets of the database. Entropy values may be used to control the selection of attributes. It is expected that an attribute with middle range entropy values may be more useful. Similar ideas have been used successfully in information retrieval.
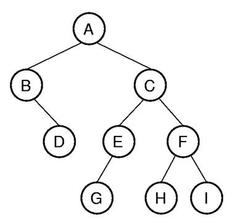
3.联合熵 (joint entropy)
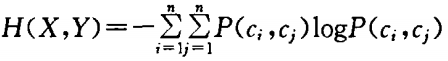
4.交叉熵
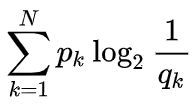
参考:https://www.zhihu.com/question/41252833
用2进制编码对所有单词进行编码
信息熵是单词编码后位数期望的最小值
即最佳编码方式为通过使用概率决定单词位置: 单词位数= -log p
但是由于实际是在制定编码方式时使用的时单词的使用频率q,这中情况下单词编码长度的期望就是交叉熵
交叉熵衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小
5.条件熵
产品条件熵能够衡量用户对于产品偏好之间的单向关联。???关联竟然不是相互的?可以理解,但首次听说
H(XIY)=H(X,Y)-H(Y)=H(X)-I(X;Y)
已知随机变量Y的条件下随机变量X的不确定性
感性理解
信息熵减去相关的部分
数学证明

6.相对熵(relative entropy)
相对熵可以衡量两个随机分布之间的距离,当两个随机分布相同时,它们的相对熵为零,当两个随机分布的差别增大时,它们的相对熵也会增大。
相对熵又被称为Kullback-Leibler散度(Kullback-Leibler divergence)或信息散度(information divergence)
相对熵表示使用理论分布拟合真实分布时产生的信息损耗
相对熵等价于两个概率分布的信息熵的差值
相对熵是两个概率分布间差异的非对称性度量
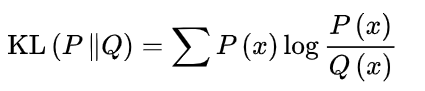
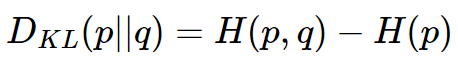
相对熵是两个概率分布间差异的非对称性度量
7.互信息 (Mutual Information)
互信息描述了随机变量之间的相关性 (依赖性)
I(X;Y)=H(X)+H(Y)-H(X,Y)
如果X和Y完全无关:H(X)+H(Y)=H(X,Y) – 信息熵的和等于联合熵
否则:H(X)+H(Y)>H(X,Y)
若无关则联合熵等于信息熵的和,若相关则联合熵小于信息熵的和
min I=0
max I=H(X)=H(Y)
I(X,X)=H(X)
The mutual information measures the decrease of uncertainty about X caused by the knowledge of Y
It is a measure of the amount of information about X contained in Y .
相似性
单向相似性是条件熵
双向相似性是互信息
单向相似性?
完全相似 <=> 条件熵=0

产品熵
取自论文《基于熵的协同过滤推荐模型》
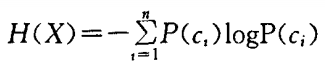
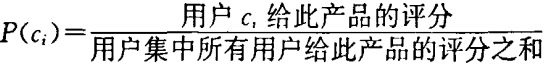

熵值高的产品:评价多,评价较为不同
熵值低的产品:价极少,评价较为一致