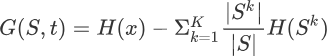1、为什么有的信息量大有的信息量小?
有些事情本来不是很确定,例如明天股票是涨还是跌。如果你告诉我明天NBA决赛开始了,这两者似乎没啥关系啊,所以你的信息对明天股票是涨是跌带来的信息量很少。但是假如NBA决赛一开始,大家都不关注股票了没人坐庄股票有99%的概率会跌,那你这句话信息量就很大,因为本来不确定的事情变得十分确定。
而有些事情本来就很确定了,例如太阳从东边升起,你再告诉我一百遍太阳从东边升起,你的话还是丝毫没有信息量的,因为这事情不能更确定了。
所以说信息量的大小跟事情不确定性的变化有关。
2、那么,不确定性的变化跟什么有关呢?
一,跟事情的可能结果的数量有关;二,跟概率有关。
先说一。
例如我们讨论太阳从哪升起。本来就只有一个结果,我们早就知道,那么无论谁传递任何信息都是没有信息量的。
当可能结果数量比较大时,我们得到的新信息才有潜力拥有大信息量。
二,单看可能结果数量不够,还要看初始的概率分布。例如一开始我就知道小明在电影院的有15*15个座位的A厅看电影。小明可以坐的位置有225个,可能结果数量算多了。可是假如我们一开始就知道小明坐在第一排的最左边的可能是99%,坐其它位置的可能性微乎其微,那么在大多数情况下,你再告诉我小明的什么信息也没有多大用,因为我们几乎确定小明坐第一排的最左边了。
3、那么,怎么衡量不确定性的变化的大小呢?怎么定义呢?
这个问题不好回答,但是假设我们已经知道这个量已经存在了,不妨就叫做信息量,那么你觉得信息量起码该满足些什么特点呢?
一,起码不是个负数吧,不然说句话还偷走信息呢~
二,起码信息量和信息量之间可以相加吧!假如你告诉我的第一句话的信息量是3,在第一句话的基础上又告诉我一句话,额外信息量是4,那么两句话信息量加起来应该等于7吧!难道还能是5是9?
三,刚刚已经提过,信息量跟概率有关系,但我们应该会觉得,信息量是连续依赖于概率的吧!就是说,某一个概率变化了0.0000001,那么这个信息量不应该变化很大。
四,刚刚也提过,信息量大小跟可能结果数量有关。假如每一个可能的结果出现的概率一样,那么对于可能结果数量多的那个事件,新信息有更大的潜力具有更大的信息量,因为初始状态下不确定性更大。
那有什么函数能满足上面四个条件呢?负的对数函数,也就是-log(x)!底数取大于1的数保证这个函数是非负的就行。前面再随便乘个正常数也行。
a. 为什么不是正的?因为假如是正的,由于x是小于等于1的数,log(x)就小于等于0了。第一个特点满足。
b. 咱们再来验证一下其他特点。三是最容易的。假如x是一个概率,那么log(x)是连续依赖于x的。done
c。四呢?假如有n个可能结果,那么出现任意一个的概率是1/n,而-log(1/n)是n的增函数,没问题。
d。最后验证二。由于-log(xy) = -log(x) -log(y),所以也是对的。学数学的同学注意,这里的y可以是给定x的条件概率,当然也可以独立于x。
By the way,这个函数是唯一的(除了还可以多乘上任意一个常数),有时间可以自己证明一下,或者查书。
ok,所以我们知道一个事件的信息量就是这个事件发生的概率的负对数。
最后终于能回到信息熵。信息熵是跟所有可能性有关系的。每个可能事件的发生都有个概率。信息熵就是平均而言发生一个事件我们得到的信息量大小。所以数学上,信息熵其实是信息量的期望。
信息论之父克劳德·香农,总结出了信息熵的三条性质:
- 单调性,即发生概率越高的事件,其所携带的信息熵越低。极端案例就是“太阳从东方升起”,因为为确定事件,所以不携带任何信息量。从信息论的角度,认为这句话没有消除任何不确定性。
- 非负性,即信息熵不能为负。这个很好理解,因为负的信息,即你得知了某个信息后,却增加了不确定性是不合逻辑的。
- 累加性,即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和。写成公式就是:
事件 同时发生,两个事件相互独立
,
那么信息熵 。
香农从数学上,严格证明了满足上述三个条件的随机变量不确定性度量函数具有唯一形式:
其中的 为常数,我们将其归一化为
即得到了信息熵公式。
补充一下,如果两个事件不相互独立,那么满足
,其中
是互信息(mutual information),代表一个随机变量包含另一个随机变量信息量的度量,这个概念在通信中用处很大。
import matplotlib.pyplot as plt import numpy as np eps=0.00001 p=np.linspace(eps,1-eps,100) H=-p*np.log(p)-(1-p)*np.log(1-p) plt.plot(p,H) plt.show()
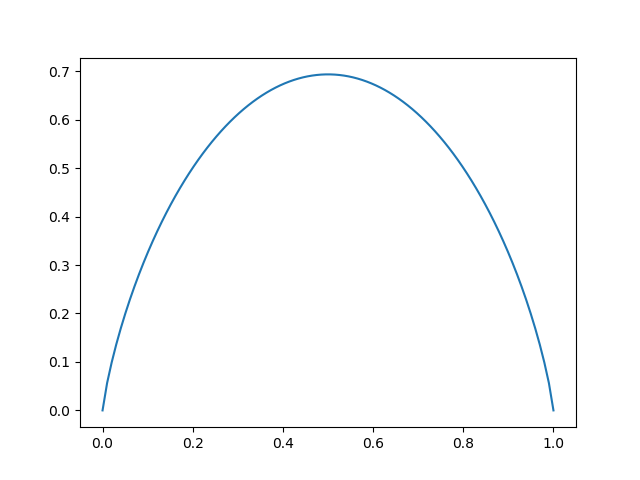
来源:知乎