引言

今天我们来探讨一下信息熵是怎么来的。

信息熵

信息的价值在于消除事件的不确定性，那事件的不确定性要怎么度量呢？答案就是信息熵(information entropy)。

比如你告诉别人你中了500万彩票，别人会大吃一惊，因为他被消除了大量的不确定性。但如果你告诉别人你没中彩票，别人基本熵没有反应，因为他估计你这小子十有八九不会中彩票。相当于你几乎没有消除他对你没有中彩票这件事的不确定性。或者说你传达的信息量太少。我们知道概率只能在0到1之间，也就是说，最好在概率为1的时候，信息量为0，且概率越小，信息量越大。后来人们发现，对数函数很符合这样的规律，某个事件的信息量与概率的关系是 $\log(\frac{1}{p})$ ，这里的对数是以2为底的， $p$ 是事件发生的概率。

上面最后这个式子是怎么来的呢？以抛硬币游戏为例，如果有一枚理想的硬币🪙，其出现正面和反面的概率相等，假设我们相隔很远，只能通过电位信号(0或1)进行交流，如何把这个🪙的结果告诉我呢。显然，此时只需要发送一个信号就可以，用1表示正面，用0表示反面。信息的价值在于消除事件的不确定性，传递一枚硬币结果的信息，帮我们消除了它是哪一个面的不确定性。

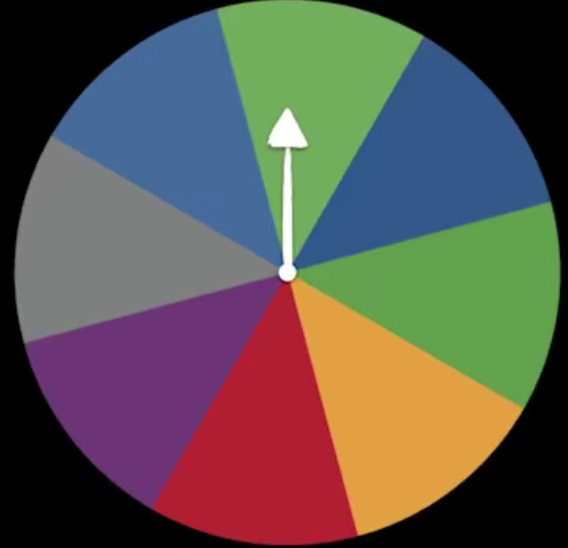
我们再来看一个转盘游戏，这个转盘被均等地分为8个区域，如果我们要把转盘的结果发送出去，那么需要多少个信号呢？答案是3个信号。

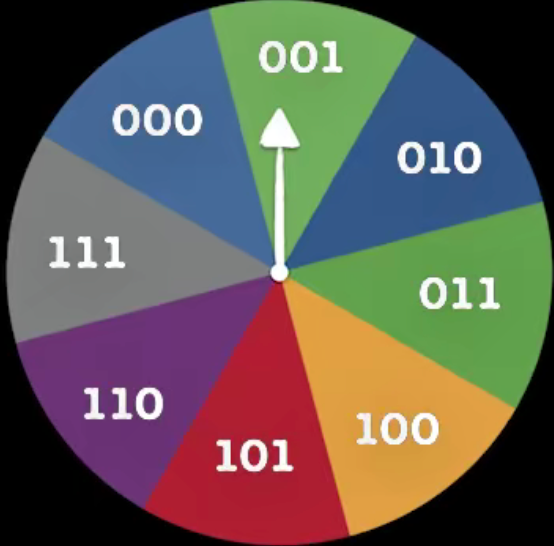
在这两个例子中，我们发现一件事情，把一个游戏系统中所有可能出现的等概率事件数量取以2为底的对数，就是我们要传递事件结果所需要的信号数量。比如在抛硬币游戏中是 $log_2(2)=1$ ，在转盘游戏中是 $log_2(8)=3$ 。这个数量就是信息量。

即 $\text{信息量}=\log(N)$ ，这里的 $N$ 是等可能事件数量。

可以把这种度量不确定性的信息量称为信息熵，但严格来说这并不是香农所说的信息熵，这只是信息熵的一个特例，即所有的事件是等可能的。我们遇到的更多情况是事件发生的可能性不一样的系统。比如现实生活中就无法制作出来正反面概率都是50%的硬币。

实际上，我们总是可以把一个事件的概率值转换为一个等可能事件系统中发生某个事件的概率。举例来说，我们总是可以把一个概率值转换为“在N个球中随机摸一个球”这个等可能事件系统中摸出某个球的概率。

假设中彩票大奖的概率很低，只有两千万分之一，我们可以把这个概率值转换为在两千万个球中摸出中奖球的概率。在这个摸球系统中，就有两千万个等可能事件。所以只需要用1除以概率值就可以想象出等可能事件系统中事件等数量，即 $N=\frac{1}{p}$ 。

假设我们有一个动了手脚的不均匀硬币，它正面朝上的概率是0.8，反面朝上的概率是0.2。

如上图，反面朝上0.2的概率可以想象有5个球的摸球系统中摸出某个球的概率。

而正面朝上0.8的概率可以想象成在有1.25个球的系统中摸出某个球的概率。我们通过想象把一个非等概率事件的系统拆成了两个等概率事件的系统。

而面对等概率事件系统，我们就可以很容易地计算它们的信息量。再把这两个想象出来的摸球系统的信息量加起来，就是这个不均匀硬币的信息量： $\log 5 + \log 1.25$ ，由于这两个我们想象出来的等概率系统本身出现的概率也不一样，因此我们需要分别乘上它们出现的概率，得 $0.2 \cdot \log 5 + 0.8 \cdot \log 1.25$ 。

如果我们用符号去抽象这些具体的值，就是
$p_1 \cdot \log \frac{1}{p_1} + p_2 \cdot \log \frac{1}{p_2} \tag{1}$
对于有更多事件的一般情况，我们可以这么表示：
$\sum_i p_i \log \frac{1}{p_i} \tag{2}$
我们整理下这个式子
$\begin{aligned} \sum_i p_i \log \frac{1}{p_i} &= \sum_i (p_i \cdot (\log1 - \log p_i)) \\ &= \sum_i - p_i \log p_i \\ &= - \sum_i p_i \log p_i \end{aligned} \tag{3}$