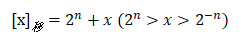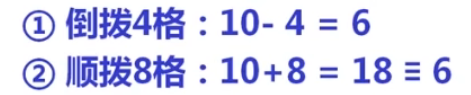这是计算机的基本知识了，一定要好好学。哈哈废话不多说，直接进入正题吧。计算机中有无符号数和有符号数两大类。
有符号数就是正负数，在计算机中正好用0和1分别去代表正和负。(ps:好多人不理解机器数和真值，机器数就是把符号数字化的数，而真值就是带正负号的数。)
1.先说说原码
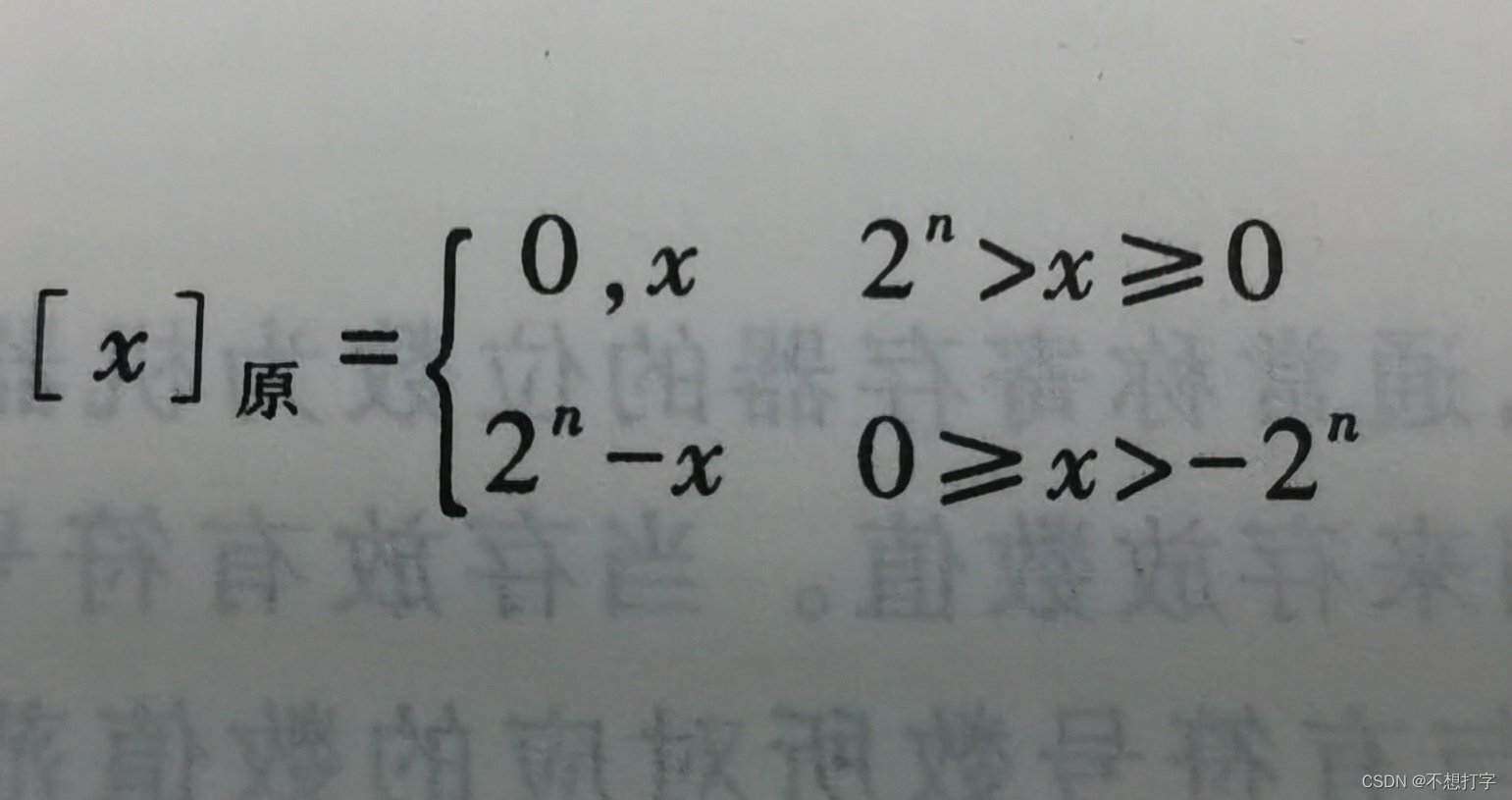整数原码
x是真值，真值大于0，原码就是它本身，只需要在它的前面放一个0就好了。
如果x小于0，那为啥要这样写呢？这个-x实际相当于|x|，2^n加上|x|就是在它前面放个1来表示符号。
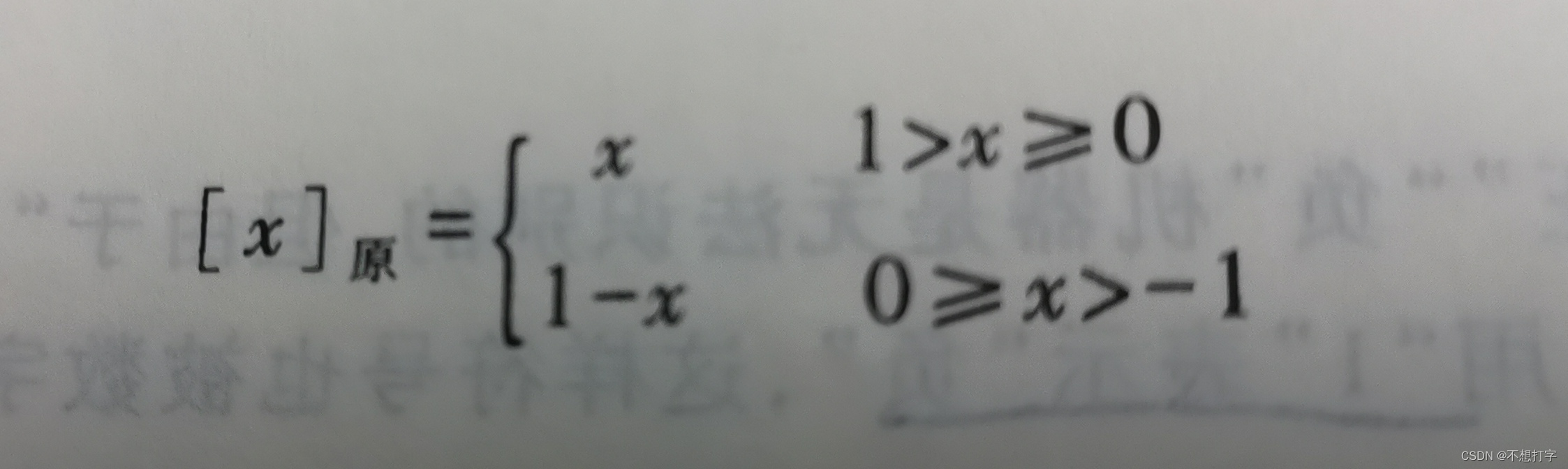小数原码
这里的关系就和上面说的道理一样了。不想说了。
举个例子
假设有x=-1011
[x]原=2^4-(-1011)=10000+1011=1，1011
2.补码
补码是为了简化运算，比如说两个一正一负的原码相加，我们不仅要考虑哪个数要大一点然后还要去看它俩和是正是负，很烦。补码就是为了解决这一麻烦事，把减法变成加法。
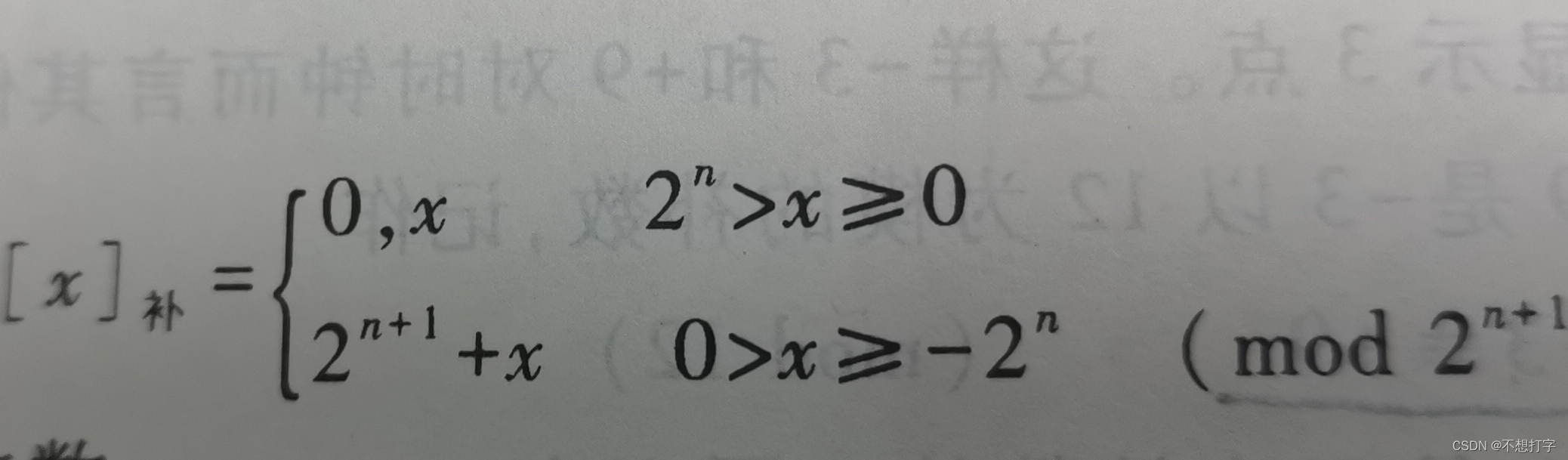整数补码
它的原理就是求补数，什么你不懂补数？好吧，我举个例子，就比如我们家里的指针表，12一圈 ，假设现在指针指向3，你想让他到5，怎么办？这时候大多数人都会让指针顺时针旋转到5 ，但你别忘了逆时针旋转也是可以的，顺时针要旋转2，逆时针旋转10，这里我们把2和-10叫做以12为模的补数。说白了负数就是求与它等价的正数，也就是它的补数。在这里尤其要弄清楚它的模是什么。
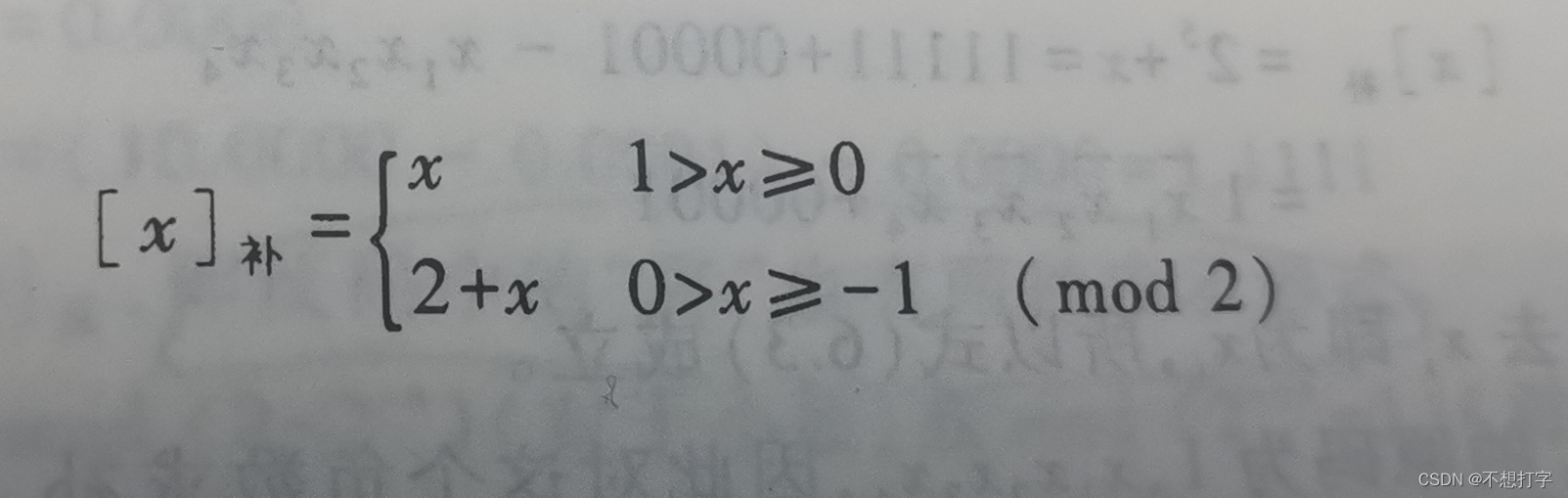小数补码
小数补码模为啥是2？你想想如果是1那是怎么回事？
举个例子
有x=-0.0110
如果模为1，[x]补=1.0000-0.0110=0.1010
小数点前是符号位变成了正的，但如果以2为模结果就是1.1010正好弥补了符号。
3.反码
反码到底有啥用啊？反码实际上是补码与原码的中间产物，不知道你有没有听过:原码求补码，符号位不变，每位取反 ，末位加一。这里每位取反就是我们的反码了，很简单。同理用补码求原码的过程中:末位减一，也得到了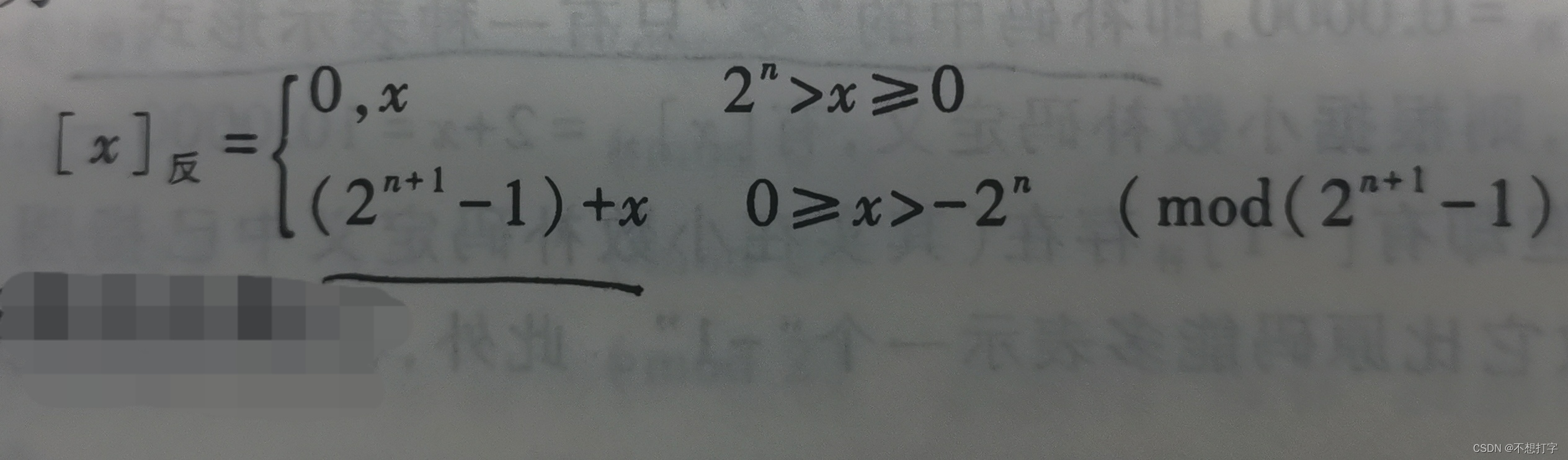反码。
整数反码
这个x大于0就不说了，说说小于0。下面这个2^(n+1)+x实际就是通过补码来求的，你可以看看补码。
举个例子
比如x=-1000
[x]反=2^5-1-1000=11111-1000=1，0111
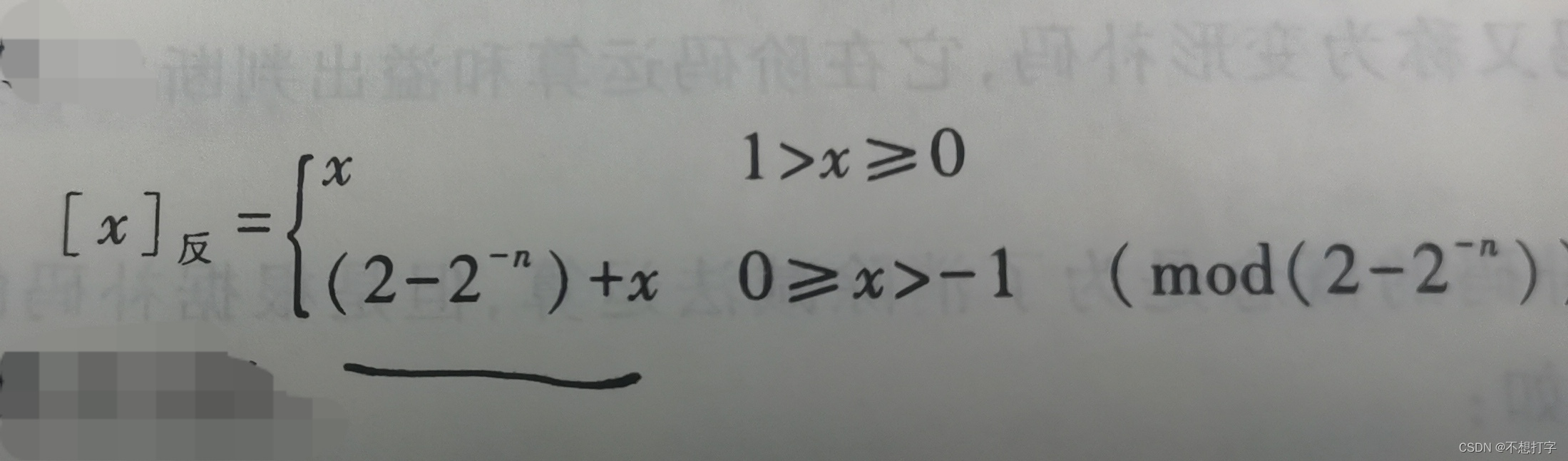小数反码
小数反码也是这个道理，在整数反码减1和小数反码中减2^-n都是一样的道理，相对于补码来说都是末尾减一。注意末尾减一不是减一。
4.移码
(终于说到移码了，口干舌燥的写了一个多小时，拿手机写的，忘了带电脑555~)
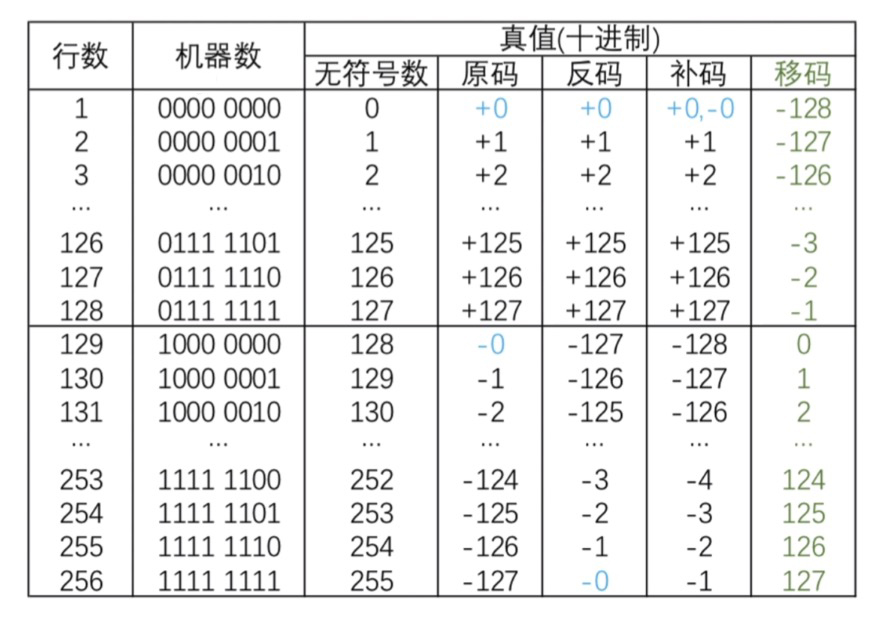
我们为啥要设置移码呢？在我们计算机中无法识别正负，我们人眼直接看到的大小机器识别不了，这就引入了移码，(顾名思义：移动的码 哈哈)
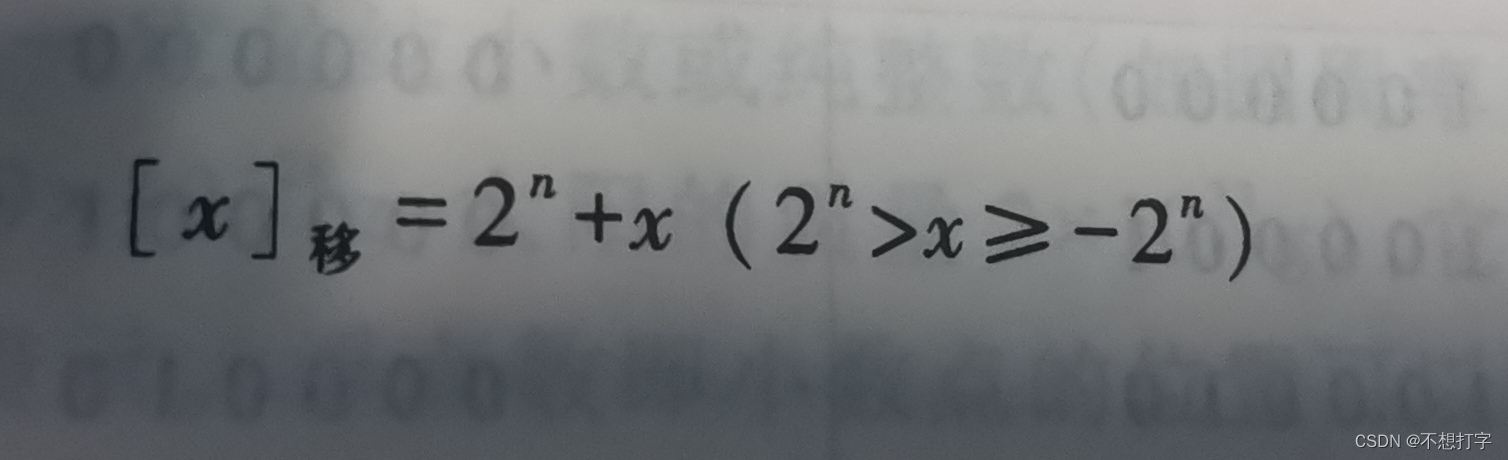
看不懂吧，我也看不懂，哈哈😃
打个比方，比如五个数abcde，有正有负，移码的思想就是把它们都平移到正半轴 ，加相同的数，但是相对大小不变，计算机一看都是正数，就好去比较它们的大小了。思想理解了，就很容易看懂公式了。
