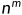计算机算法设计与分析
最近发现一些刷题的网站,牛客、力扣,很适合用来熟悉算法和语言知识点。
第1章 算法概述
1.1 算法与程序
算法 是解决问题的一种方法或一个过程。
严格地说,算法是由若干条指令组成的有穷序列,且满足下述4条性质。
- 输入
- 输出:至少产生一个量作为输出。
- 确定性:每条指令清晰、无歧义。
- 有限性:执行次数、时间有限
程序和算法不同。程序不一定满足上述4条性质。
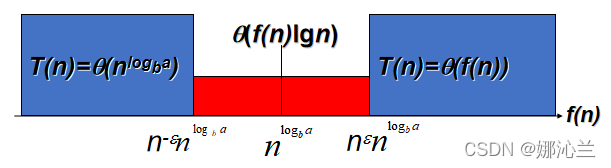
1.2 算法复杂性分析
最坏时间复杂度:O;时间上界;
1.3 NP完全性理论
可在多项式时间内求解的判断问题构成 P类问题。
第2章 递归与分治策略
分治法的思想:将一个难以直接解决的大问题分解为一些规模较小的相同问题,以便各个击破,分而治之。
2.1 递归的概念
直接或间接调用自身的算法称为递归算法。
【例2-1】阶乘函数。
阶乘函数可递归的定义为:
n! = 1 ,n=0
= n(n-1)! , n>0
递归式的第一式给出了这个函数的 初始值,是非递归定义的(直接给出)。每个递归函数都必须有非递归定义的初始值,否则会一直递归下去。
递归式的第二式用较小的自变量的函数值来表示较大自变量的函数值的方法来定义n的阶乘。
用代码表示:
int factorial(int n){if (n==0)return 1;elsereturn n*factorial(n-1);}【例2-6】Hanoi塔问题
问题略。
可用递归方法解决:
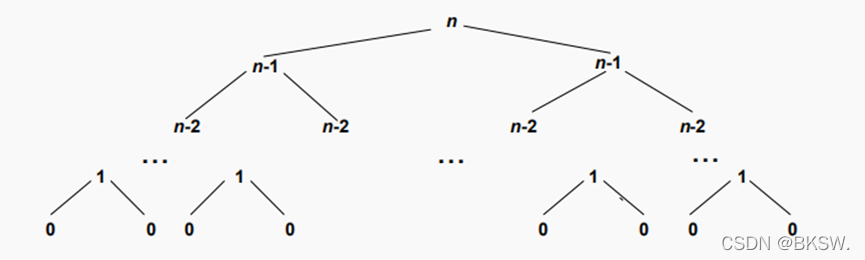
当n=1时,只要将当前盘子从当前位置塔a放在目标塔b即可。
当n>1时,需要利用塔c作为辅助塔,将n-1个圆盘移动到c上,然后将剩下的最大圆盘移动到b上。即n个圆盘的问题变成两次n-1个圆盘的问题。
用代码表示:
//4个参数依次是剩余数量,起点,终点,中间点void hanoi(int n, char a, char b, char c){if (n==1)move(a,b);else{hanoi(n-1,a,c,b);move(a,b);hanoi(n-1,c,b,a);}}void move(char begin,char end){cout<<begin<<"--->"<<end<<"\n";}2.2 分治法的基本思想
分治法的基本思想是将一个规模为n的问题分解为k个规模较小的子问题,子问题之间相互独立且与原问题类型相同。
2.3二分搜索技术
二分搜索是分治的典型例子。
给定已排好序(为了简便,设为升序排序)的n个元素a[0,n-1],要在其中找到一特定元素x。
如果用顺序搜索(从头开始依次往后比较),最坏情况需要n次比较;
二分搜索采用分治策略,最坏情况用O(logn)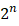 时间完成。
时间完成。
二分搜索的基本思想:将n个元素分成数量基本相同的两份,取a[n/2]与x比较,如果x 等于a[n/2],则找到,算法终止;如果x<a[n/2],则x较小,只要在数组a的左半部继续搜索;
如果x>a[n/2],则x较大,只要在数组a的右半边继续搜索。
/*二分搜索 */template<class Type>int BinarySearch(Type a[],const Type& x, int n){int left = 0;int right = n-1;while(left<=right){int middle = (left+right)/2;if (x==a[middle])return middle;if (x>a[middle])left = middle+1;if (x<a[middle])right = middle-1;}return -1;}//递归形式int BinarySearch(int a[],int x,int left,int right){if(left>right)return -1;int middle = (left+right)/2;if (x==a[middle])return middle;if(x<a[middle])return BinarySearch(a,x,left,middle-1);if(x>a[middle])return BinarySearch(a,x,middle+1,right);}2.4 大整数的乘法
有二进制整数X和Y,要计算X * Y,
将X分成两份:A、B,
Y分解两份:C、D
XY = (A*2n/2![]() +B)(C*2n/2
+B)(C*2n/2![]() +D)
+D)
=AC*2n![]() +((A-B)(D-C)+AC+BD)* 2n/2
+((A-B)(D-C)+AC+BD)* 2n/2![]() +BD //利用数学变形,减少乘法次数
+BD //利用数学变形,减少乘法次数
2.5 Strassen矩阵乘法
(直接分解再乘并不能减少乘法次数,通过一些变形增加加减法次数,减少乘法次数)。
2.7 合并排序
用分治策略对N个元素进行排序。
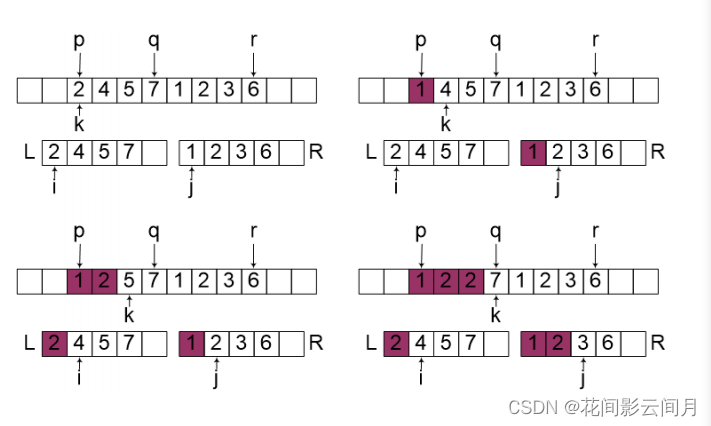
基本思想:将待排序的n个元素分成大小大致相同的两个子集,分别对两个子集进行排序,然后再合并两个子集。
template<class Type>void MergeSort(Type a[],Type b[], int left, int right) {if (left < right) {int i = (left + right) / 2;MergeSort(a, b,left, i);MergeSort(a, b,i + 1, right);Merge(a, b, left, i, right); //合并到b数组Copy(a, b, left, right); //复制回a数组}template<class Type>void Merge(Type c[], Type d[], int l, int m, int r) { //合并c[l:m]和c[m+1:r]到d[l:r]int i = l, j = m + 1;int pos = l;while ((i <= m) && (j <= r)) {if (c[i] <= c[j])d[pos++] = c[i++];elsed[pos++] = c[j++];if (i > m) { //第1个数组放完了,直接把第2个数组剩下的放到dfor (int q = j; q <= r; q++)d[pos++] = c[q];}if (j > r) { //第2个数组放完了,直接把第1个数组剩下的放到dfor (int q = i; q <= m; q++)d[pos++] = c[q];}}}template<class Type>void Copy(Type a[], Type b[], int left, int right) {for (int i = left; i <= right; i++)a[i] = b[i];}2.8 快速排序
对于数组a[p:r]按三个 步骤排序:
1. 分解(Divide):以a[p]为基准元素,a[p:r]分解为3段:a[p:q-1].a[q]]和a[q+1:r]
使得a[p:q-1]中的元素都<=a[q] , a[q+1:r]>=a[q],下标q在划分过程中确定。
2.递归求解(Conquer):使用递归对a[p:q-1]和a[q+1:r]进行排序。
3.合并(Merge):a[p:q-1]和a[q+1:r]排序好后,不需要进行操作就已经排好序了。
template<class Type>void QuickSort(Type a[],int p,int r){if(p<r){int q = Partition(a,p,r);QuickSort(a,p,q-1);QuickSort(a,q+1,r);}}template<class Type>int Partition(Type a[],int p, int r){int i=p+1, j =r;Type x = a[p];while(true){while(a[i]<x && i<r) //直到找到a[i]>=xi++;while(a[j]>x) //直到找到a[j]<=xj--;if(i>=j)break;swap(a[i],a[j]); //交换a[i],a[j],使得左边都小于x,右边>x}swap(a[p],a[j]);return j;}