系列文章目录
第一章 算法设计与分析基础知识
第二章 算法的分治策略
第三章 算法的动态规划
第四章 算法的贪心法
……
@[TOC](这里写目录标题) # 一级目录 ## 二级目录 ### 三级目录
参考教材
《算法设计与分析(第2版)》是由屈婉玲、刘田、张立昂、王捍贫编著,2016年清华大学出版社出版的21世纪大学本科计算机专业系列教材、普通高等教育“十一五”国家级规划教材。该教材适合作为大学计算机科学与技术、软件工程、信息安全、信息与计算科学等专业本科生和研究生的教学用书,也可以作为从事实际问题求解的算法设计与分析工作的科技人员的参考。

一、算法的由来
1 算法的由来
公元9世纪,波斯著名的数学家、天文学家、地理学 家阿尔·花拉子密在公元825年写成《印度数字算术》一书,对于 印度-阿拉伯数字系统在中东及欧洲的传播起到了重要作用。 该书被翻译成拉丁语“Algoritmi de numeroIndorum”, 花拉子密的拉丁文音译即为“算法”(Algorithm)一词的由来。
2 算法的历史
① 约公元前300年欧几里得提出了辗转相除法,用于计算两个整数的最大公约数, 其被记录在 欧几里得《几何原本》中
② 公元前1世纪,我国的第一本 “算法 ”书《周髀算经》出世
③ 魏晋时期,数学家刘徽在《九章算术注》中首创割圆术,内接正多边形去无限逼近圆,并以此求取圆周率的方法。
④ 唐高宗显庆元年(公元656年),规定将十部汉、唐一千多年间的十部著名数学著作作为国家最高学府的算学教科书,用以进行数学教育和考试,后世通称为《算经十书》。
3 为什么要学算法
数学王子 高斯的故事:
求: 1+ 2 + 3 + 4 + 5 + ⋯+ 100 =?
方式1(普通的方式): 对数据进行累加
1+2 =3
3+3 =6
6+4 =10
……
4950 + 100 = 5050
方式2(高斯算法): (1+100)* 50 = 5050
由上面的案例,我们可以得到如下结论:
求解同一问题通常存在多种方法,其效率可能不同,
所以需要我们分析比较算法运行效率,判断哪个算法更高效。
二、算法的基本概念
1 算法定义
给定计算问题,算法是一系列良定义(定义明确无歧义)的计算步骤,逐一执行计算步骤(计算机可实现的指令)即可得预期的输出。
举例:
比如我们平时在代码编写过程中比较常见的排序问题:
输入包含𝒐个数字的数组 < 𝒂1 ,𝒂2,…,𝒂n >输出升序排列的数组
< 𝒂ʹ1,𝒂ʹ2,…,𝒂ʹn>满足𝒂ʹ1≤ 𝒂ʹ2≤ ⋯ ≤ 𝒂ʹn
输入: [24, 17, 40, 28, 13, 14, 22, 32, 40,21, 48, 4, 47, 8, 37, 18]使用选择排序将上述数组升序排列
算法代表着用系统的方法描述解决问题的策略机制,算法提供的是一种策略,不是唯一的答案(比如排序我们有冒泡排序、快速排序、选择排序等,它们都可以实现数组排序操作,但是效率不尽相同),所以算法无对错,只有好和不好(所以才有算法分析)。
2 算法的性质
有穷性、确定性、可行性
(1)有穷性:算法必须在有限个计算步骤后终止
反面示例:以前面的选择排序来说:
输入: 给定一个数组
步骤x: 不断交换首尾元素的位置
分析: 不断交换什么时候才结束?没有终结的条件
正面案例:
第一次遍历找到最小元素
第二次在剩余数组中遍历找到次小元素
……
第n次在剩余数组中遍历找到第n小元素
分析: 遍历次数至多与数组元素个数相同
(2)确定性:算法必须是没有歧义的
反面示例:
输入: 给定一个数组
步骤x: 交换两个数的位置
分析: 没有具体指明是哪两个数
正面案例:
第一次遍历找到最小元素
第二次在剩余数组中遍历找到次小元素
……
第n次在剩余数组中遍历找到第n小元素
分析:每一个步骤要做什么都是确定的
(3)可行性:可以机械地一步一步执行基本操作步骤
反面示例:
输入: 给定一个数组
步骤x: 将大元素放数组后部,小元素放数组前部
分析: 描述含糊,不可拆解为基本操作步骤
正面案例:
第一次遍历找到最小元素
第二次在剩余数组中遍历找到次小元素
……
第n次在剩余数组中遍历找到第n小元素
分析: 算法可一步步地执行完成
二、算法的伪码描述
1 什么是伪码?
伪代码(Pseudocode)是一种非正式的,类似于英语结构的,用于描述模块结构图的语言。人们在用不同的编程语言实现同一个算法时意识到,他们的实现(注意:这里是实现,不是功能)很不同。尤其是对于那些熟练于不同编程语言的程序员要理解一个(用其他编程语言编写的程序的)功能时可能很难,因为程序语言的形式限制了程序员对程序关键部分的理解。这样伪代码就应运而生了。伪代码提供了更多的设计信息,每一个模块的描述都必须与设计结构图一起出现。
2 为什么要用伪码?
使用伪代码的目的是使被描述的算法可以容易地以任何一种编程语言(Pascal,C,Java等)实现。因此,伪代码必须结构清晰、代码简单、可读性好,并且类似自然语言。 介于自然语言与编程语言之间。以编程语言的书写形式指明算法职能。使用伪代码, 不用拘泥于具体实现。相比程序语言(例如Java, C++,C, Dephi 等等)它更类似自然语言。它是半角式化、不标准的语言。可以将整个算法运行过程的结构用接近自然语言的形式(可以使用任何一种你熟悉的文字,关键是把程序的意思表达出来)描述出来。
3 怎么用伪码?
(1)伪代码语法规则
类Pascal语言的伪代码的语法规则是:在伪代码中,每一条指令占一行(else if,例外) 。指令后不跟任何符号(Pascal和C中语句要以分号结尾)。书写上的“缩进”表示程序中的分支程序结构。这种缩进风格也适用于if-then-else语句。用缩进取代传统Pascal中的begin和end语句来表示程序的块结构可以大大提高代码的清晰性。
(2)具体符号:
赋值语句:←
分支语句: f-.then…else…
循环语句: while, for, repeat until
转向语句: goto
输出语句: return
调用
注释: //…
(3)举例:
① C语言:输入3个数,打印输出其中最大的数。可用如下的伪代码表示:
Begin(算法开始)
输入 A,B,C
IF A>B 则 A→Max
否则 B→Max
IF C>Max 则 C→Max
Print Max
End (算法结束
②
if 九点以前 then
do 私人事务;
if 9点到18点 then
工作;
else
下班;
end if
三、算法的数学基础
在讨论算法设计与分析技术之前,我们需要介绍一些相关的数学知识,包括函数的渐进的的界的定义与性质、算法分析中常用的证明方法、序列求和的技术以及递推方程的求解。
1 大O表示法
统计算法运行速度, 应统一运行机器,应考虑算法运行的最坏的情况,那么这样的话可以得到一个结论: 算法运行时间仅依赖于问题输入规模𝒏,表示为𝑻(𝒏)
int sum(int n){int s=0; //1int i=1; //1int j=1; //1for(;i<=n;i++){// 2nj=1; //nfor(;j<=n;j++){ //2(n*n)s=s+i+j; //n*n}}return s;}
上述代码中,算法的运行速度为: T(n) = 3 + 3n + 3
此时如果我们发现n的规模无限扩大时, 前面的系数、3n、3 这些都对T(n)结果造成的影响是非常小的,可以忽略。所以此时T(n) 可以简化为: T(n) = n2这是坏的情况下,该算法的运行时间。
在计算机科学中,一般我们使用大O表示法来描述一个算法的最差情况, 定义为T[n] = O(f(n))
T(n): 代码执行时间
n: 数据规模
f(n): 代表计算代码总执行时间的函数,比如上面的n2
O: 代码的执行时间与f(n)表达式成正比
一般来说当n无限大时,我们只关注高阶,像低阶、常量都可以忽略
大 O 时间复杂度实际上并不具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,所以,也叫作渐进时间复杂度(asymptotic timecomplexity),简称时间复杂度。
二、算法的数学基础
1 函数的渐近的界
(1)大O符号
定义:设f和g是定义域为自然数集 N 上的函数. 若存在正数 c 和 n0,使得对一切 n >= n0有0 =< f(n) =< c g(n)成立, 则称 f(n) 的渐近的上界是 g(n), 记作f (n) = O(g(n))
举例:
设 f(n) = n2 + n,则
f(n)=O(n2),取 c = 2,n0 =1 即可
f(n)=O(n3),取 c = 1,n0 =2 即可
f (n) = O(g(n)) ,f(n)的阶不高于g(n)的阶.
可能存在多个正数c,只要指出一个即可.
对前面有限个值可以不满足不等式.
常函数可以写作O(1).
(2)大Ω符号
定义:设 f和 g是定义域为自然数集 N 上的函数. 若存在正数 c 和 n0,使得对一切 n >= n0有 0 =< cg(n) =< f(n)成立, 则称 f(n) 的渐近的下界是 g(n),记作 f (n) = Ω(g(n))
举例:
设 f(n) = n2 + n,则
f(n) = (n2), 取 c = 1, n0 =1即可
f(n) = (100n), 取 c=1/100, n0 =1即可
f (n)= (g(n)),f(n)的阶不低于g(n)的阶.
可能存在多个正数c,指出一个即可.
对前面有限个 n 值可以不满足上述不等式.
(3)小o符号
定义 设 f 和 g是定义域为自然数集 N 上的函数. 若对于任意正数 c 都存在 n0,使得对一切 n >= n0有 0 =< f(n) < c g(n)成立, 则记作f (n) = o(g(n))
举例:
f(n)=n2+n,则
f(n)=o(n3)
c>=1显然成立,因为n2+n<cn3(n0=2)
任给1>c >0, 取 n0 > [2/c] 即可. 因为 cn >= cn0 > 2(当n >= n)
n2+n < 2n2 < cn3
f (n) = o(g(n)) , f(n)的阶低于g(n)的阶
对不同正数c, n0不一样. c越小n0越大.
对前面有限个 n 值可以不满足不等式.
(4)小ω符号
定义:设 f 和 g是定义域为自然数集 N 上的函数. 若对于任意正数 c 都存在 n0,使 得对一切 n >= n0有 0 =< cg(n) < f(n)
成立, 则记作 f (n) = ω(g(n))
举例:
设 f (n) = n2 + n,则
f (n) = ω(n),
不能写 f (n) = ω (n2),因为取 c = 2,不存在n0 使得对一切 n n0有下式成立
c n2 = 2n2< n2 + n
f (n)=ω (g(n)), f (n)的阶高于g(n) 的阶.
对不同的正数c, n0不等,c 越大n0 越大.
对前面有限个 n 值可以 不满足不等式.
(5)Θ 符号
若 f (n) = O (g(n)) 且 f (n) = Θ (g(n)), 则记作
f (n) = (g(n))
例子:f(n) =n2 + n, g(n) =100n2,那么有
f(n)=Θ (g(n))
f(n) 的阶与 g(n) 的阶相等.
对前面有限个n 值可以不满足条件.
2 求和的方法
(1)序列求和
等差、等比数列与调和级数
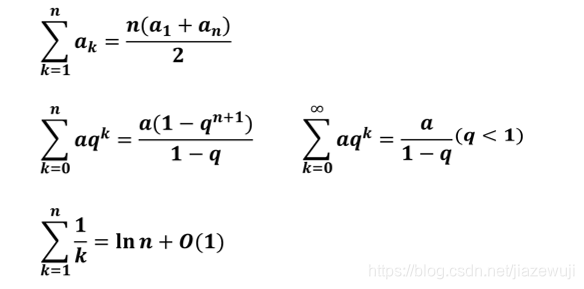
(2)估计和式的界
① 估计和式上界的放大法


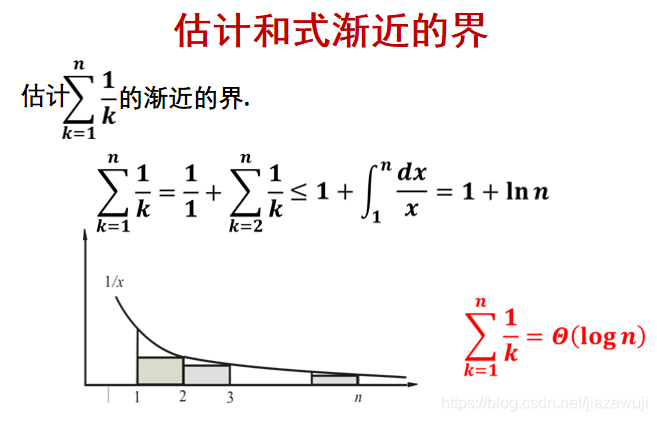
② 估计和式渐进的界
3 递推方程求解方法
(1)定义
如果数列{an}的第n项与它前一项或几项的关系可以用一个式子来表示,那么这个公式叫做这个数列的递推公式。
举例:汉诺塔问题的递归算法
算法 Hanoi (A, C, n) // n个盘子A到C
if n=1 then move (A, C) // 1个盘子A到C
else Hanoi (A, B, n-1)move (A, C)Hanoi (B, C, n-1)
(2)不同方法的递归
① 迭代法
不断用递推方程的右部替换左部
每次替换,随着 n 的降低在和式中多出一项
直到出现初值停止迭代
将初值代入并对和式求和
可用数学归纳法验证解的正确性
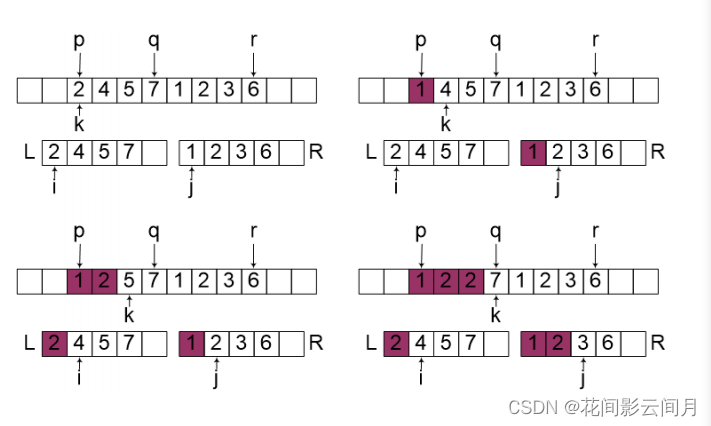
② 递归树
递归树是迭代过程的一种图像表述。递归树往往被用于求解递归方程, 它的求解表示比一般的迭代会更加的简洁与清晰。
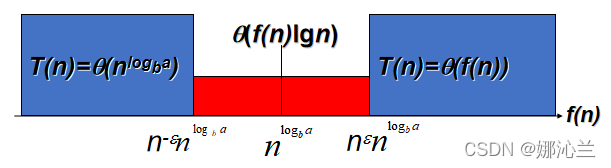
③ 主定理


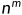






![[逐笔数据分析工具分享]如何分析股票逐笔数据](https://img-blog.csdnimg.cn/20210412143407722.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2FucWluZzcxNQ==,size_16,color_FFFFFF,t_70)