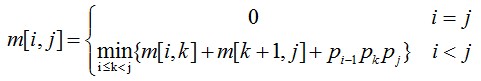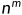目录
- 算法分析题
- 1.1 函数的渐进表达式
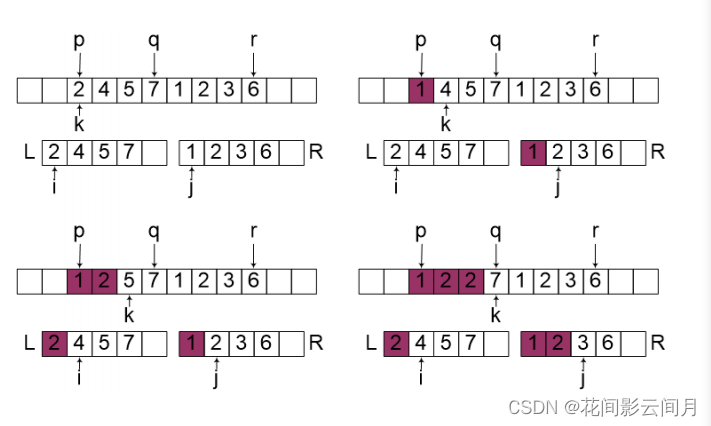
- 1.3 证明对于任何实数x和整数a,b,n:
- 1.7 函数渐进阶
- 算法实现题
- 1.1 统计数字问题
- 1.3 最多约数问题
算法分析题
1.1 函数的渐进表达式
求下列函数的渐近表达式:3n2+10n; n2/10+2n; 21+1/n; logn3; 10log3n

1.3 证明对于任何实数x和整数a,b,n:


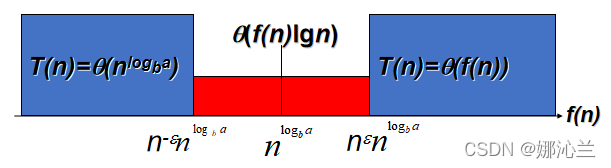
1.7 函数渐进阶
对于下列各组函数f(n)和g(n),确定f(n)=O(g(n))或f(n)=Ω(g(n))或f(n)=Θ(g(n)),并简述理由。
(1)f(n)=logn2; g(n)=logn+5
(2)f(n)=logn2; g(n)=√n
(3)f(n)=n; g(n)=log2 n
(4)f(n)=nlogn+n; g(n)=logn
(5)f(n)=10; g(n)=log10
(6)f(n)=log2 n; g(n)=logn
(7)f(n)=2n; g(n)=100n2
(8)f(n)=2n; g(n)=3n

算法实现题
1.1 统计数字问题
问题描述:一本书的页码从自然数1开始顺序编码直到自然数n。书的页码按照通常的习惯编排,每个页码都不含多余的前导数字0。例如,第6页用数字6表示,而不是06或006等。数字计数问题是要求对给定书的页码n,计算出书的全部页码分别用多少次数字0,1,2,…,9。
编程任务:给定表示书的总页码的十进制整数n(1≤n≤≤10^9)。编程计算书的全部页码中分别用到多少次数字0, 1, 2,…,9。
数据输入:输入数据由文件名的input.txt的文本文件提供。每个文件只有1行,给出表示书的总页码的整数n。
结果输出:程序运行结束时,将计算结果输出到文件output.txt中。输出文件共有10行,在第k行输出页码中用到数字k-1的次数,k=1,2,…,10。
输入文件示例 输出文件示例
Input.txt output.txt
11 1
4
1
1
1
1
1
1
1
1
# -*- coding: utf-8 -*-
# @Time : 2021/3/16 10:59
# @Author : 拔牙不打麻药
# @FileName: HW1_test1.py
# @Software: PyCharmimport osinput_address = "./input.txt"
output_address = "./output.txt"
# 打开写好的output.txt 里面是11,表示11页
with open(input_address,"r") as f:for i in f.readlines():pages = iarray=[[0,1,2,3,4,5,6,7,8,9],[0,0,0,0,0,0,0,0,0,0]]#从第一页到pages页分别求每个数字
for i in range(1,int(pages)+1):j=iwhile j > 0:k = j % 10#print(k)m = 0for m in range(10):if array[0][m] == k:array[1][m] = array[1][m]+1j = j // 10#输出到output.txt
with open(output_address,"w") as f:for i in range (10):f.write(str(array[1][i]))f.write("\n")

1.3 最多约数问题
问题描述:正整数x的约数是能整除x的正整数。正整数x的约数个数记为div(x)。例如,1,2,5,10都是正整数10的约数,且div(10)=4。设a和b是2个正整数,a≤b,找出a和b之间约数个数最多的数x。
编程任务:对于给定的2个正整数a≤b,编程计算a和b之间约数个数最多的数。
数据输入:输入数据由文件名为input.txt的文本文件提供。文件的第1行有2个正整数a和b。
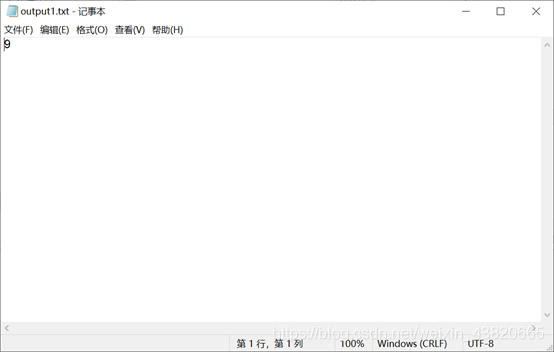
结果输出:程序运行结束时,若找到的a和b之间的约数个数最多的数是x,则将div(x)输出到文件out.txt中。
输入文件示例 输出文件示例
Input.txt output.txt
1 36 9
# -*- coding: utf-8 -*-
# @Time : 2021/3/17 18:44
# @Author : 拔牙不打麻药
# @FileName: HW1_test2.py
# @Software: PyCharminput_address = "./input1.txt"
output_address ="./output1.txt"with open(input_address,"r") as f:str1 = str(f.readline())a,b = str1.split(" ")
a = int(a)
b = int(b)
max = 0 #目前拥有公约数最多的数字
div = 0 #目前拥有最多的公约数数目for i in range(a,b+1):flag = 0number = ifor j in range(1,number+1):if number % j == 0:flag += 1if flag > div:max = numberdiv = flagwith open(output_address,"w") as f:f.write(str(div))
字有点丑…以上是我自己做的,可能会有很多错误,等阳老师讲过题再过来改嘎嘎嘎。今天为了写算法的作业晚晚下班了15551
3.22更新
已经订正了,比不出阶的大小可还行。