写完 Java 的我又开始对 算法设计与分析 下手了(✿◡‿◡)
内容主要是以 北京大学 屈婉玲老师的 MOOC 视频来写的,视频共是十周的内容,我决定用 五 篇博客完成。
温馨提示:这个课程不仅适用于 算法设计与分析 的学习,也非常适用于 数学建模 的学习,如果是学习 数学建模的基础部分,前两周的内容是非常适合的,如果要进一步学习 建模思想,建议把这十周视频好好看一遍。( •̀ ω •́ )y
我们还是先来看一下这十周视频的思维导图:
在这篇博客中写的是前两周的内容:基础知识。
第一周
排序问题的计算复杂度
如下表:
NP-hard 问题(NP难问题):
货郎问题、0-1背包问题、双机调度问题等。
至今没有找到有效算法(我们指的有效算法就是运行时间是 n 的多项式,比如 n 的平方, n 的立方等等),现有的算法的运行时间是输入规模的指数或更高阶函数。
那以后能不能找到多项式时间的算法呢?至今没有人能够证明对于这类问题不存在多项式时间的算法。
算法的两种时间复杂度
最坏情况下的时间复杂度 W(n):
算法求解输入规模为 n 的实例所需要的最长时间。
平均情况下的时间复杂度 A(n):
在给定同样规模为 n 的输入实例的概率分布下,算法求解这些实例所需要的平均时间。
算法的伪码描述

五种表示函数的阶的符号
具体的定义就不说了,我想你们会有更详细的资料,我们直接来看怎么把这五种表示函数的阶的符号记得更牢,并且不会记错。
大 O 符号:f(n) = O( g(n) )
称 f(n) 的渐近的上界是 g(n),f(n) 的阶不高于 g(n) 的阶。(类似于小于等于符号)
大 Ω 符号:f(n) = Ω( g(n) )
称 f(n) 的渐近的下界是 g(n),f(n) 的阶不低于 g(n) 的阶。(类似于大于等于符号)
小 o 符号:f(n) = o( g(n) ),f(n) 的阶低于 g(n) 的阶。(类似于小于符号)
小 w 符号:f(n) = w( g(n) ),f(n) 的阶高于 g(n) 的阶。(类似于大于符号)
θ 符号
若 f(n) = O( g(n) ) 且 f(n) = Ω( g(n) ) ,则记作 f(n) = θ( g(n) ) (类似于等于符号)
有关函数渐近的界的定理
定理1:函数的阶与极限的关系
定理2:函数的阶之间的关系具有传递性
定理3:有限个函数和的阶与原函数的阶的关系
定理的证明过程用到阶的符号的定义,我在这里就省略了。
我们来说一下常用的一些重要结果:
(1):多项式函数的阶低于指数函数的阶
(2):对数函数的阶低于幂函数的阶(幂函数也就是多项式函数)
由定理1 和定理2 我们可得到估计函数的阶的两个方法:计算极限、阶具有传递性。
算法的时间复杂度是各步操作时间之和,在常数步的情况下取最高阶的函数即可。
基本函数类
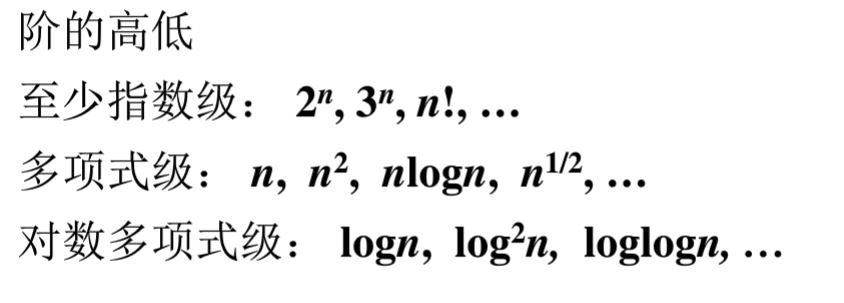
对数函数
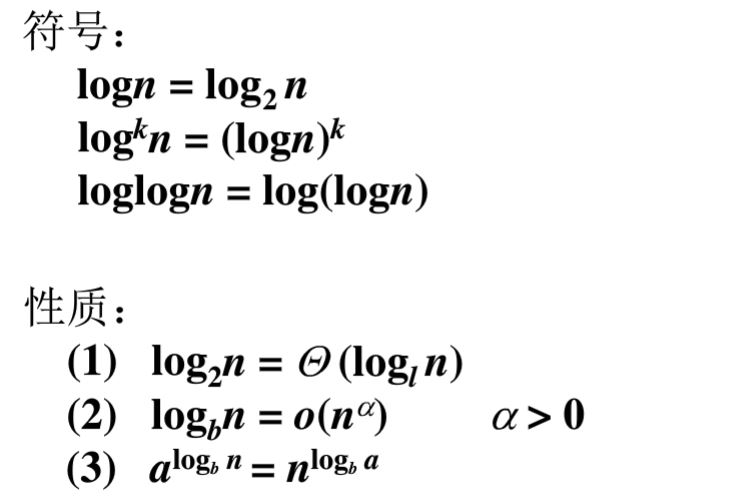
说明:
(1)logn 没有写底时代表的是 log 以2为底的对数
(2) 对于对数函数,它们的底并不重要,因为我们常常关注的是函数的阶,所以对于以任何常数为底的对数函数它们都是同阶的。
(3)a 的 log 以b为底的n 等于 n 的 log 以b为底的a。(两者相等的证明:等号两边同时取对数即可)如果看等号前面哪个表达式,n在指数位置的地方,看起来很像一个指数函数。其实并不是,因为前一个表达式等于后一个表达式,而后一个表达式是多项式函数,所以 a 的 log 以b为底的n 是一个多项式函数。一般,我们遇到左边的这种表达式,都是写为右边的表达式,
斯特林公式

斯特林公式的应用:估计搜索空间的大小
取整函数

第一周小结:五种符号+六个公式
1.五种表示函数的阶的符号 是重点,每一个符号代表的意义一点要记住的。
2.在对数函数和斯特林公式中,里面由一些重要的函数,包括:
第二周
序列求和基本公式

估计序列和
(1)放大法求上界:
(2)用积分做和式的渐近的界
递推方程

说明:
(1)实际上递推方程,表达的是这个序列的项和它前边的项的依赖关系。
(2)递推方程的求解:给定关于序列的递推方程和初值,求出第 n 个项的通项公式的过程。
迭代法求解递推方程
直接迭代,代入初值,然后求和:
例子:
换元迭代:对递推方程和初值进行换元,然后求和,求和后进行相反换元,得到原始递推方程的解。
例子:
验证方法——数学归纳法。
差消法化简高阶递推方程
对于递推方程的求解基本方法是迭代,如果这个依赖关系比较复杂的时候,直接迭代就会非常困难。这个时候,我们就要尽量化简,把高阶递推方程先用差消法化简为一阶方程。然后继续迭代。
例子:
递归树
递归树是迭代的图形表示。
(1)递归树的概念:
(2)迭代在递归树中的表示:
说明:
递归树和迭代有着紧密的联系,是迭代的模型。
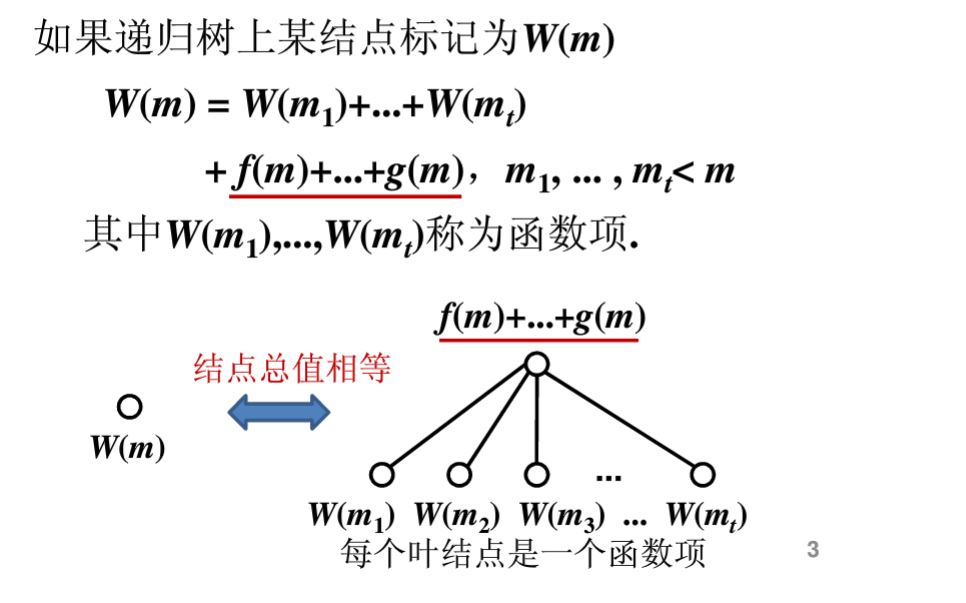
假定上面的是递归方程,左边是规模为 m 的工作量 W(m) 。右边出现它的一些子问题(带W()的项,我们称为函数项),划分规划需要的工作量(称为非函数项)。
把函数项作为儿子,非函数项作为根,就形成上面的一层迭代。
(3)递归树的生成规则:
(4)如何利用递归树求解递推方程:
由上面的迭代在递归树中的表示,可以看出对递归树上所有的项进行求和就是迭代后方程的解。
主定理及其证明
主定理是求解递推方程的另外一种方法。
主定理的应用背景:
主定理的内容:
说明:
看到递推公式,
第一步:看是否满足主定理应用的条件,也就是看递推公式是否是主定理递推公式的形式;
第二步:拿 f(n) 分别与三种情况进行比较,看符合那一种,就可以估计出递推方程的解。
注意:主定理的第 3 种情况的条件,比前两种情况多一个。
证明过程在此省略,我们需要记住的是主定理的内容,还有可以应用主定理的条件。
第二周小结:序列求和方法+递推方程求解
序列求和的方法:
(1)用基本公式求解;
(2)放大法就上界;
(3)用积分做和式渐近的界。
递推方程的求解:
(1)迭代法(包括 直接迭代和换元迭代);
(2)差消法化简高阶递推方程;
(3)用递归树求解递推方程;
(4)用主定理求解递推方程。
例子总结:





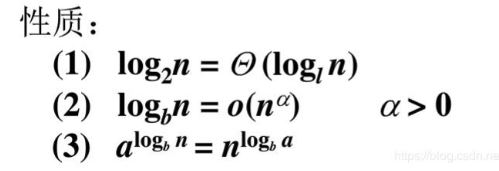
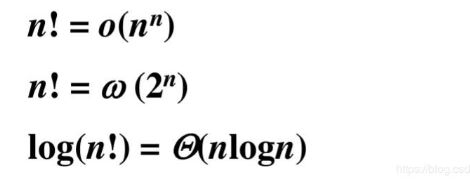






















![[逐笔数据分析工具分享]如何分析股票逐笔数据](https://img-blog.csdnimg.cn/20210412143407722.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2FucWluZzcxNQ==,size_16,color_FFFFFF,t_70)