这篇博客主要用来记录一下现代机器人学里面比较基础也比较重要的一些知识点，所有内容均仅仅记录是什么而不写为什么，因为虽然是基础，但机器人学本身就是一个高度交叉科目，需要很多前置知识堆砌，这里不方便一一解释，但懂得自然懂，不懂的稍微补一下相关知识问题也不大。

坐标转换与机械臂运动学

坐标转换可以说是机器人学的地基，也是重中之重，后面很多轨迹生成方法和控制方案都没有一个标准，那些实际上也都是围绕坐标转换来建立的。说白了整个机器人运动学就是不停地坐标转换，或者将其他诸如理论力学的科目与坐标转换结合起来变来变去。但是在机器人学里有自己的一套描述坐标转换的方式，不同于飞行器和航天飞行器还有计算机视觉里面的坐标变换。
在其他地方都有的欧拉角变换、轴-角和四元数这些这里就不写了，这里直接上机器人学里最伟大的发明——DH(Denavit-Hartenberg)参数法变换。

Denavit-Hartenberg参数（也称为DH参数）是与特定约定相关联的四个参数，用于将参考系附加到空间运动链或机器人操纵器的链接上。DH参数是雅克·丹纳维特（Jacques Denavit）和理查德·哈腾贝格（Richard Hartenberg）在1955年发表的，用来标准化空间链接的坐标系。理查德·保罗（Richard Paul）在1981年证明了其在机器人系统运动学分析中的价值。尽管已经开发了许多用于连接参考框架的约定，但Denavit-Hartenberg约定仍然是迄今为止最简洁的方法。

为什么DH参数如此牛逼，做过安装矩阵或者一些空间转换的都知道，三维空间任意两点的转换是有六个自由度的，但是丹纳维特和哈腾贝格两位大佬通过对链式结构特定的建系方法，将六个自由度减少到四个自由度，别小看这减少的两个自由度，这将导致很多无法实现的计算量真正得以实现，大大降低了对链式结构的解算难度。

说了这么多废话，直接上DH参数下的变化矩阵:

四个参数分别为：

ai（蓝色），αi（绿色），di（紫色），θi（红色）。

ai = 沿Xi轴，从Zi移动到Zi+1的距离
αi = 沿Xi轴，从Zi旋转到Zi+1的角度
di = 沿Xi轴，从Xi-1移动到Xi的距离
θi = 绕Zi轴，从Xi-1旋转到Xi的角度

建系原则：

选取Zi轴与第i个旋转轴重合，Xi轴垂直于Zi轴于Zi+1轴所在的平面，指向Zi+1轴，θi 与αi取右手定则为正方向，Yi轴根据Xi和Zi轴取右手定则决定。ai的长度为Zi到Zi+1的最短距离，也就是沿着Xi的这根线被Zi和Zi+1截取的长度。

如图所示：

在4X4矩阵里面的最后一行是没有意义的，补上的两行，很多地方也把转换矩阵写成是一个3X4的矩阵，这都没什么太大问题。左上角3X3是方位角转换矩阵，右边的3X1这一列就是位移变换。

而机械臂运动学里的速度和角速度转换也无非就是些坐标转换内容而已，直接上公式：

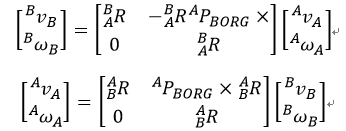
这里面要注意的一点就是角速度在转化过程中是可以直接根据坐标系的方向线性叠加的，而线速度要附加一部分由于前坐标系转动而产生的速度。

雅克比矩阵

雅克比矩阵是用时变线性来代替非线性关系的重要工具，在机器人学中用雅克比矩阵来进行关节空间和笛卡尔空间的转换。

一个n自由度的机械手，正运动学方程可以写为：

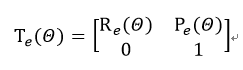
e表示末端执行器的位置和方向随着关节矩阵的变化而变化：

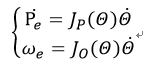
Pe和we表示末端执行器的线速度和角速度。

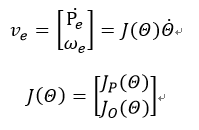
其中：


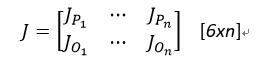
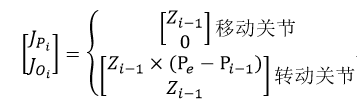
其中Zi-1由旋转矩阵的第三列给出：

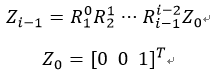
其中Pe通过变换举证T的第四列的前三个元素给出：

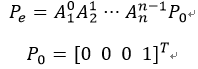
同理：

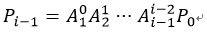
雅克比矩阵在使用的时候也没有这么刻板，重要的是在理解了原理以后就可以灵活运用了。

机械臂逆向动力学（牛顿欧拉递推）

链式结构或者机械臂结构的动力学是机器人学里非常难的也是最核心的部分，好的控制方案和好的规划方案往往都来自于一个好而精确的动力学模型。但很可惜的是，由于链式结构的高耦合性，机械臂的正向动力学是无法直接得出的，动力学数学建模的过程往往先通过正向运动学由内向外推导出各个机械臂的角速度和线速度，获取各个机械臂的物理特性，再通过牛顿和欧拉方程从力学角度从最外层机械臂向最内层机械臂逐步推导，这个过程叫做逆向动力学。最终得到的结果是已知各关节的角度角加速度角速度来求出各关节所需要的扭矩。逆向动力学虽然不能直接用于仿真机械臂的运动状态，但是可以用于规划和控制。

具体过程如下：

①运动学外推：

②牛顿-欧拉内推过程：

外推过程实际上就是由内而外的运动学推导，内推过程实际上也就是由外向内逐步根据牛顿欧拉方程推导出力和力矩，最后得到关节力矩，红色表示下一个机械臂相关的运动学变量，蓝色表示当前机械臂相关的运动学变量，至于质量和惯性矩阵参数什么的这里就不记录了。

最终可以得到一个概括总体的机械臂位形空间方程：

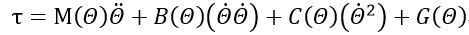
等号右端为已知的关节空间相关的角度角速度角加速度项，左侧为根据逆向动力学得到的所需扭矩。

其中M为操作臂nXn阶质量矩阵，B为哥氏力系数矩阵，C为nXn阶离心力系数矩阵，G是nX1阶重力梯度矩阵。

机械臂正向动力学

刚刚说过直接建立正向动力学模型很难，但正向动力学是用来仿真的必要条件，建立正向模型的意义非凡。动力学正解问题包括在初始位置和初始速度已知的情况下，对t＞to，根据给定的关节转矩，确定关节加速度，通过对关节加速度数值积分得出角速度和角度。如下式：

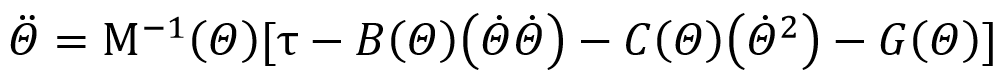
但是难度在于无法从刚刚的牛顿欧拉推导过程中直接得到状态方程里的每一项，各项之间也是高度耦合的，没有办法对某一项分离出来求逆，这就是难以得到正向动力学的主要原因。这里就需要利用到上一节的逆向动力学和一些小技巧了。

正向动力学模型建立方法和步骤：

①先令所有关节角加速度为0，此时等式中的M矩阵消失，于是得到：

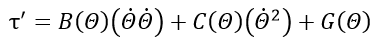
这一步的目的是得到与关节角加速度无关项的大小。

②取角加速度矩阵的第一行为1，其他行全为0，并取所有关节角加速度都为0，代入各关节角的位置（此时并没有得到真实的关节角位置，仅保留入口），得到M矩阵的第一行；接着取角加速度矩阵的第二行为1，其他行为0，并取所有关节角加速度为0，继续代入关节角位移矩阵，得到M矩阵的第二行；依此类推，取角加速度矩阵的第n行为1，其他行为0，得到的是M的第n行。将n个M矩阵的行向量拼接成完整的M矩阵，最后用数值计算方法求得M矩阵的逆矩阵，根据下式求得关节角加速度矩阵：

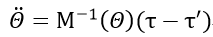
③用求得的关节角加速度矩阵数值积分得到角速度矩阵，再积分得到角度矩阵，将角速度矩阵代入第①步的式子中，角度矩阵代入第②步的式子中，整个动力学模型就完整而封闭了。

整个过程只利用到了正向的动力学模型，不管是用代码还是用什么框图实现的正向模型只要复制n+1遍就得到了逆向动力学模型，是不是有一种无中生有的赶脚，但别小看这个无中生有的建模过程，这是机器人学里一篇非常著名的论文，有兴趣的可以去看看。

运动轨迹生成

运动轨迹这里相较与其他几个部分稍微简单点也灵活一些，没有特别固定的方法，这里仅仅简单记录S型曲线的生成方案，其他的可以举一反三。

一般在S曲线运动轨迹下，规定好起始位置和目标位置后，假设起始加速度和目标位置的加速度都为0，因此有边界条件：

S型曲线为次数至少是3次的多项式构成，于是设四个常系数，得到三次多项式运动轨迹：

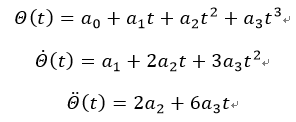
反解出四个常系数，得到：

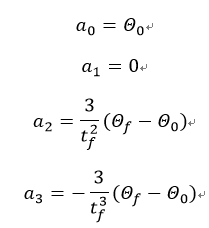
每一个关节都根据自己的需要和边界条件解出四个常系数，就可以得知在指定时间内的角加速度，角速度和角位移的值，根据这些值又可以配合前面的逆向动力学得到应该施加的关节扭矩，就可以让机械臂走出一个简单的S曲线了。这里必须要注意一点，这里还没有加入控制系统，仅有轨迹规划的情况下真实的位移速度和加速度必须与规划出来的结果严格相等，否则无法进行曲线运动，有偏差的情况下就需要借助控制的力量了。

动力学轨迹跟踪控制

规划完关节空间的运动轨迹之后必不可少的就是跟踪运动轨迹，本篇文章以逆向动力学控制为例简要介绍一种控制方案。

参考结构为非线行多变量系统控制。n个关节的机械手动力学模型表达式如下所示：

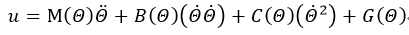
可以记为

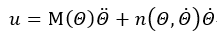
可以找到一个控制向量u，该向量是系统状态的函数，可以以此实现线性形式的输入/输出关系，换句话说就是可以通过非线行的状态反馈实现系统动力学的精确线性化，而非近似线性化。通过系统动力学的特定形式，使发现线性化控制器的可能性得以保证。实际上上式的方程对控制u是线性的，且该方程含有满秩矩阵M，对任意机械臂的位形都可以求逆。

可以用下式表示机械臂的状态函数：

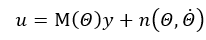
所以系统可以这么表示：

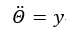
其中y表示新的输入向量，其表达式尚未确定；所得框图如下：

所以刚刚的状态函数中的非线行控制律采用逆动力学控制的形式，因为该控制律是基于机械手动力学逆解计算的。控制系统相对新输入y是线性解耦的，换句话说，在双积分器关系下元素yi只影响关节变量qi，与其他关机的运动无关。

所以机械臂的控制问题就简化成了找到稳定控制律y。为此选：

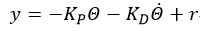
得到二阶系统方程：

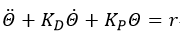
假定矩阵Kp和KD正定，上式渐进稳定。令Kp和KD为如下对角阵：


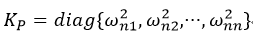
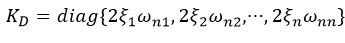
得到解耦系统。参考因素ri只影响关节变量qi，二者是自然频率wni和阻尼比决定的二阶输入输出关系。

给定任意期望轨迹Qd，为保证输出Q跟踪该轨迹，选择：

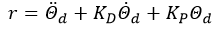
实际上，把上式代入之前的二阶系统方程，可以得到相似的二阶微分方程：

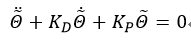
该式表示跟踪轨迹的过程中，位置误差的动态变化，该误差只有当Q(0)和dQ(0)不为0的时候存在，收敛速度和所选矩阵相关。

整个过程可以看做如下框图：

但这种控制方法并不是非常理想的，因为忽略了动态项的影响，所以自然会带来由非完全补偿造成的敏感性和鲁棒性问题。更多优秀的控制方法可以自己看书查论文。

喜大普奔完结撒花~