之前我对卡方检验的了解都是一知半解的,即知道作用是对离散变量分布差异的比较,根据期望频数和观察频数的差异计算出来一个卡方值,之后根据自由度和显著性水平查卡方分布对应的临界值,比较大小得出有无明显差异的结论。
一般我们都说单元格期望数最好不小于5,也就是期望频数不小于5,但这里我个问题:
为什么要求期望频数不小于5?假设期望频数小于5会有什么后果?
这两个问题相信不少人都不是很清楚,今天我们就来讲下这两个问题。
标准化残差是将残差与期望频数平方根相除得到的,太小的期望频数很可能任性地放大了残差,进而导致卡方统计量过大,有可能造成“弃真”错误(第1类错误),所以,期望频数接近最小的硬性指标5时,就需要检查相应单元格的残差时不是特别大。
换句话说,假如我们做出了接受原假设的结论,即使此时有些期望频数小于5也无所谓,因为他们只会导致更大的卡方值。
而当我们做出了拒绝原假设的结论时,就需要特别注意是不是有些期望频数小于5,这个时候我们有可能会因为有些期望频数小于5这个因素过大的计算了卡方值,进而造成“弃真”错误。此时需要重点关注相应单元格的残差时不是特别大。
1.导入数据
import pandas as pd
data=pd.read_clipboard()
data.head()
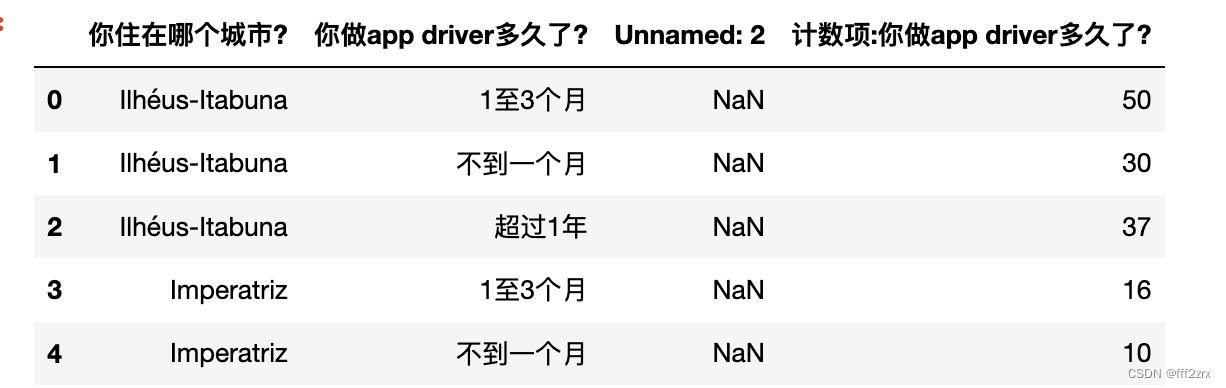
2.统计观察频数
data.columns=['city','answer','score','driver_num']
data1=pd.pivot_table(data=data,index=['answer'],columns=['city'],values=['driver_num'],\aggfunc='sum',fill_value=0)
data1.columns=data1.columns.droplevel(level=0)
data1.reset_index(drop=False,inplace=True)
data2=data1.melt(id_vars=['answer'],value_name='观察频数')
data2.head()

3.统计各组总数目和总体的期望分布
rate=(data2.groupby(['answer'])['观察频数'].sum()/data2.groupby(['answer'])['观察频数'].sum().sum()).reset_index()
rate.columns=['answer','rate']
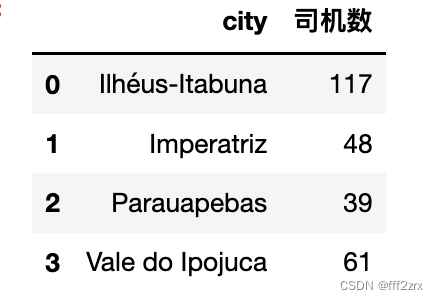
group_sum=data2.groupby(['city'])['观察频数'].sum().reset_index()
group_sum.columns=['city','司机数']
group_sum
4.计算期望频数和卡方值
import math
data3=pd.merge(data2,group_sum,on=['city'],how='left')
data3=pd.merge(data3,rate,on=['answer'],how='left')
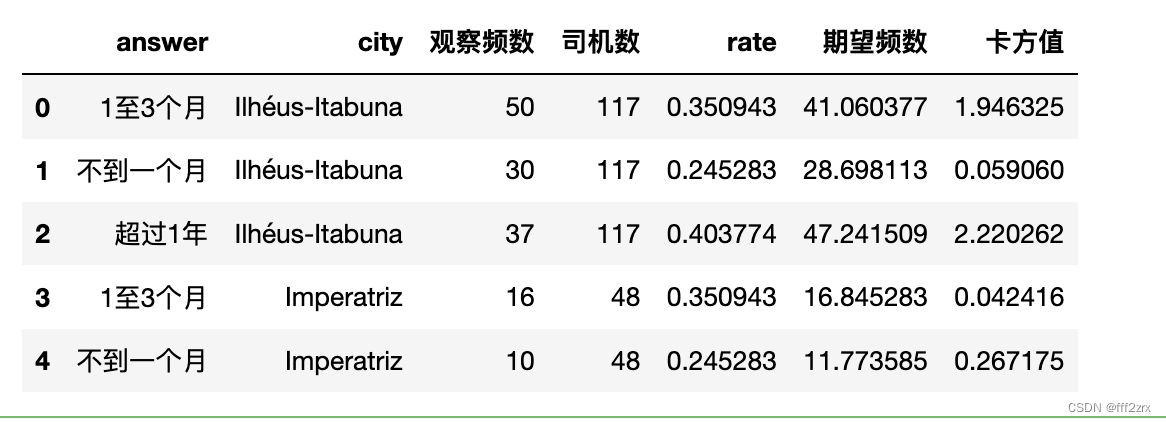
data3['期望频数']=data3['司机数']*data3['rate']
data3['卡方值']=data3.apply(lambda x: math.pow((x.期望频数-x.观察频数),2)/x.期望频数,axis=1)
data3['残差']=data3.apply(lambda x: (x.观察频数-x.期望频数),axis=1)
data3.head()
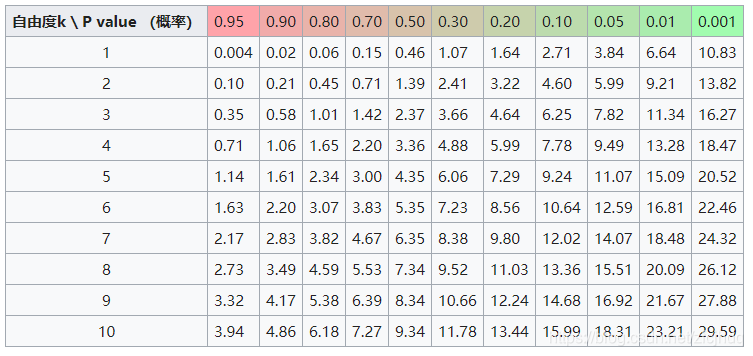
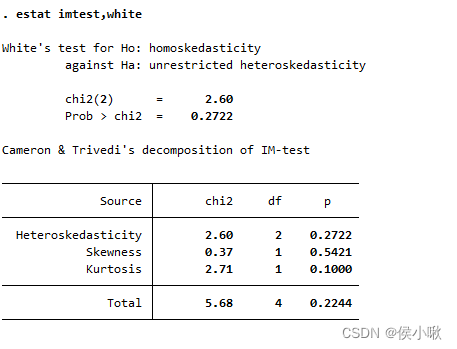
5.根据自由度查表得出结论
卡方分布表查询
data3['卡方值'].sum()

由于此时是拒绝了原假设,需要特别注意有无期望频数小于5的情况。若有,还需要关注对应的残差的大小情况。
6.两两比较
由于3个城市整体来看并不是无明显差异,所以可以进一步两两比较,这个时候可以直接调用
python的chi2_contingency函数用于计算。
def chi2_contingency_my(data_input,city1,city2):values1=data_input[data_input['city']==city1]['观察频数'].tolist()values2=data_input[data_input['city']==city2]['观察频数'].tolist()data = np.array([values1, values2])try:kf = chi2_contingency(data)print('--------------')print('chisq-statistic=%.4f, p-value=%.4f, df=%i expected_frep=%s'%kf)#第一个值为卡方值,第二个值为P值,第三个值为自由度,第四个为与原数据数组同维度的对应理论值if kf[1]<0.05:print("{}与{}的选择存在显著差异".format(city1,city2))else:print("{}与{}的选择无显著差异".format(city1,city2))except:print('--------------')print("{}与{}的某选项均为0,无法计算".format(city1,city2))
city_list=data3['city'].unique().tolist()
for i in range(0,len(city_list)-1):for j in range(i+1,len(city_list)):chi2_contingency_my(data3,city_list[i],city_list[j])