目录
一、画残差图
二、BP检验
(一)手动编制函数进行BP检验
(二)调用statsmodels的函数进行BP检验
三、怀特检验
(一)手动编制函数进行White检验
(二)调用statsmodels的函数进行White检验
四、Goldfeld-Quandt 检验
(一)手动编制函数进行GQ检验
(二)调用statsmodels的函数进行GQ检验
此文章首发于公众号:Python for Finance
链接:【Python计量】异方差性的检验
我们以伍德里奇《计量经济学导论:现代方法》的”第8章 异方差性“的案例8.4为例,使用HPRICE1中的数据来检验一个简单的住房价格方程中的异方差性。利用所有变量的水平值所估计的方程是:
import wooldridge as woo
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import patsy as pthprice1 = woo.dataWoo('hprice1')#建立回归模型:
reg = smf.ols(formula='price ~ lotsize + sqrft + bdrms', data=hprice1)
results = reg.fit()
print(results.summary())
一、画残差图
由于残差可视为扰动项的实现值,故可通过残差的波动来考察是否存在异方差性。具体可以看:
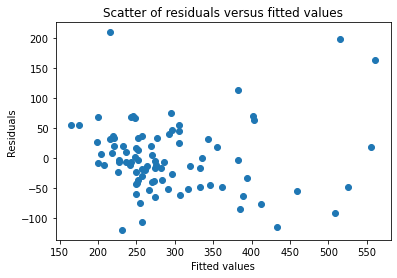
(1)残差与拟合值的散点图
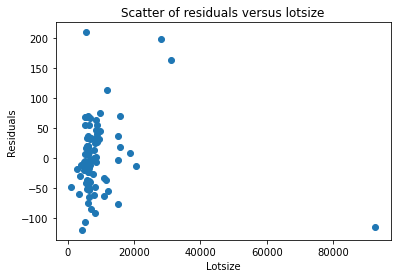
(2)残差与某个解释变量的散点图
import matplotlib.pyplot as pltres=results.resid #从OLS回归模型中获取残差
fitted=results.fittedvalues #从OLS回归模型中获取拟合值#残差与拟合值的散点图
plt.figure(1)
plt.scatter(fitted,res)
plt.xlabel('Fitted values')
plt.ylabel('Residuals')
plt.title('Scatter of residuals versus fitted values')
plt.show()
#残差与被解释变量lotsize的散点图
plt.figure(2)
plt.scatter(hprice1['lotsize'],res)
plt.xlabel('Lotsize')
plt.ylabel('Residuals')
plt.title('Scatter of residuals versus lotsize')
plt.show()
二、BP检验
假设回归模型如下:
假设同方差性,即
由于我们假定u的条件期望值为0,所以)),因而同方差性的原假设就等价于:
为了检验是否违背了同方差假定,我们想检验是否与一个或多个解释变量相关。若是错误的,则给定自变量,的期望值可能是x的函数。一个简单的方法就是假定一个线性函数:
同方差的原假设就是:
为检验解释的自变量的整体显著性,可用F或LM统计量来检验
(一)手动编制函数进行BP检验
hprice1['resid_sq'] = results.resid ** 2 #定义残差的平方
reg_resid = smf.ols(formula='resid_sq ~ lotsize + sqrft + bdrms', data=hprice1)
results_resid = reg_resid.fit()
bp_F_statistic = results_resid.fvalue
bp_F_pval = results_resid.f_pvalue
print(f'bp检验的F统计量: {bp_F_statistic}')
print(f'bp检验的F统计量对应的p值: {bp_F_pval}')
'''
bp检验的F统计量: 5.338919363241433
bp检验的F统计量对应的p值: 0.002047744420936033
'''
F统计量5.34,对应的p值0.002,拒绝原假设;即模型存在异方差性。
(二)调用statsmodels的函数进行BP检验
从statsmodels库的stats子模块的diagnostic工具中导入het_breuschpagan
from statsmodels.stats.diagnostic import het_breuschpagan #BP检验
het_breuschpagan函数的参数意义及返回结果
het_breuschpagan(resid, exog_het, robust=True)
参数介绍:
resid:残差
exog_het:用于bp检验的自变量返回值:
lm : LM统计量值
lm_pvalue : LM统计量的p值,若p值小于显著性水平,则拒绝残差方差为常数的原假设,即存在异方差性
fvalue : F统计量值,用来检验残差平方项与自变量之间是否独立,如果独立则表明不存在异方差性
f_pvalue : F统计量对应的p值,若p值小于显著性水平,则拒绝**残差方差为常数的原假设**,即存在异方差性
对上述模型做BP检验,代码如下:
result_bp_test = het_breuschpagan(results.resid, reg.exog)
bp_lm_statistic = result_bp_test[0]
bp_lm_pval = result_bp_test[1]
bp_F_statistic= result_bp_test[2]
bp_F_pval = result_bp_test[3]
bp_test_output=pd.Series(result_bp_test[0:4],index=['bp_lm_statistic','bp_lm_pval','bp_F_statistic','bp_F_pval'])
print(bp_test_output)'''
bp_lm_statistic 14.092386
bp_lm_pval 0.002782
bp_F_statistic 5.338919
bp_F_pval 0.002048
dtype: float64
'''我们可以在het_breuschpagan函数的基础上,编制一个能返回异方差检验结果的函数。
def bp_test(res, X):result_bp_test = sm.stats.diagnostic.het_breuschpagan(res, X)bp_lm_statistic = result_bp_test[0]bp_lm_pval = result_bp_test[1]bp_F_statistic= result_bp_test[2]bp_F_pval = result_bp_test[3]bp_test_output=pd.Series(result_bp_test[0:4],index=['bp_lm_statistic','bp_lm_pval','bp_F_statistic','bp_F_pval']) return bp_test_output
进行BP检验时,调用上述函数即可。
bp_test_output=bp_test(results.resid, reg.exog)
print(bp_test_output)
'''
bp_lm_statistic 14.092386
bp_lm_pval 0.002782
bp_F_statistic 5.338919
bp_F_pval 0.002048
dtype: float64
'''
F统计量5.34,对应的p值0.002,拒绝原假设;LM统计量14.09,对应的p值0.0028,拒绝原假设。即模型存在异方差性。
三、怀特检验
BP检验假设条件方差函数为线性函数,忽略了高次项。为此,怀特检验再BP检验的辅助回归中加入了所有的二次项(含平方项和交叉项)。
当模型包含k=3个自变量时,怀特检验则基于如下估计:
对原假设进行F检验或LM检验。
(一)手动编制函数进行White检验
hprice1['resid_sq'] = results.resid ** 2
reg_resid = smf.ols(formula='resid_sq ~ lotsize*sqrft*bdrms+I(lotsize**2)+I(sqrft **2)+I(bdrms**2)-lotsize:sqrft:bdrms', data=hprice1)
results_resid = reg_resid.fit()
white_F_statistic = results_resid.fvalue
white_F_pval = results_resid.f_pvalue
print(f'white检验的F统计量: {white_F_statistic}')
print(f'white检验的F统计量对应的p值: {white_F_pval}')
'''
white检验的F统计量: 5.386953445894593
white检验的F统计量对应的p值: 1.0129388323900798e-05
'''
F统计量5.39,对应的p值接近于0,拒绝原假设;即模型存在异方差性。
(二)调用statsmodels的函数进行White检验
从statsmodels库的stats子模块的diagnostic工具中导入het_white
from statsmodels.stats.diagnostic import het_white #怀特检验
het_white函数的参数意义及返回结果
het_white(resid, exog)
参数介绍:
resid:残差
exog_het:用于white检验的自变量(只需要自变量的一阶形式,函数自动加入平方和交互作用项进行回归)返回值:
lm : LM统计量值
lm_pvalue : LM统计量的p值,若p值小于显著性水平,则拒绝残差方差为常数的原假设,即存在异方差性
fvalue : F统计量值,用来检验残差平方项与自变量之间是否独立,如果独立则表明不存在异方差性
f_pvalue : F统计量对应的p值,若p值小于显著性水平,则拒绝**残差方差为常数的原假设**,即存在异方差性
对上述模型做怀特检验,代码如下:
def white_test(res, X):result_bp_test = sm.stats.diagnostic.het_white(res, X)bp_lm_statistic = result_bp_test[0]bp_lm_pval = result_bp_test[1]bp_F_statistic= result_bp_test[2]bp_F_pval = result_bp_test[3]white_test_output=pd.Series(result_bp_test[0:4],index=['white_lm_statistic','white_lm_pval','white_F_statistic','white_F_pval']) return white_test_outputwhite_test_output=white_test(results.resid,reg.exog)
print(white_test_output)
'''
white_lm_statistic 33.731658
white_lm_pval 0.000100
white_F_statistic 5.386953
white_F_pval 0.000010
dtype: float64
'''
LM统计量F统计量5.39,对应的p值接近于0,拒绝原假设;LM统计量14.09,对应的p值0.0028,拒绝原假设。即模型存在异方差性。
四、Goldfeld-Quandt 检验
Goldfeld-Quandt 检验由Goldfeld和Quandt于1965年提出。这种检验的思想是以引起异方差的解释变量的大小为顺序,去掉中间若干个值,从而把整个样本分为两个子样本。用两个子样本分别进行回归,并计算残差平方和,用两个残差平方和构造检验异方差的统计量。
(一)手动编制函数进行GQ检验
#按解释变量的大小做升序排列
hprice2=hprice1.sort_values(by="lotsize", ascending=True)#按指定的列(by=)排序,ascending=False为降序,True为升序#去掉中间部分的值,分别选取前30组观测值和后30组观测值分别进行一元线性回归
#前30组一元线性回归
reg_first30= smf.ols(formula='price ~ lotsize +sqrft+bdrms',data=hprice2.iloc[0:30,:])
results_first30=reg_first30.fit()
#后30组一元线性回归
reg_last30= smf.ols(formula='price ~ lotsize +sqrft+bdrms',data=hprice2.iloc[58:,:])
results_last30=reg_last30.fit()#F检验
F=results_last30.mse_resid/results_first30.mse_resid
print("F=",F)'''
F= 1.658048702954414
'''
若我们需要前30组一元线性回归和后30组一元线性回归结果,则输入代码:
print(results_first30.summary())
print(results_last30.summary())
'''OLS Regression Results
==============================================================================
Dep. Variable: price R-squared: 0.119
Model: OLS Adj. R-squared: 0.017
Method: Least Squares F-statistic: 1.170
Date: Fri, 22 Apr 2022 Prob (F-statistic): 0.340
Time: 14:14:53 Log-Likelihood: -160.84
No. Observations: 30 AIC: 329.7
Df Residuals: 26 BIC: 335.3
Df Model: 3
Covariance Type: nonrobust
==============================================================================coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 94.3425 100.295 0.941 0.356 -111.817 300.502
lotsize 0.0098 0.010 0.981 0.336 -0.011 0.030
sqrft 0.0613 0.033 1.844 0.077 -0.007 0.130
bdrms -2.0513 15.173 -0.135 0.894 -33.241 29.138
==============================================================================
Omnibus: 19.188 Durbin-Watson: 1.611
Prob(Omnibus): 0.000 Jarque-Bera (JB): 36.110
Skew: 1.299 Prob(JB): 1.44e-08
Kurtosis: 7.705 Cond. No. 5.40e+04
==============================================================================Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 5.4e+04. This might indicate that there are
strong multicollinearity or other numerical problems.OLS Regression Results
==============================================================================
Dep. Variable: price R-squared: 0.720
Model: OLS Adj. R-squared: 0.688
Method: Least Squares F-statistic: 22.30
Date: Fri, 22 Apr 2022 Prob (F-statistic): 2.33e-07
Time: 14:15:42 Log-Likelihood: -168.43
No. Observations: 30 AIC: 344.9
Df Residuals: 26 BIC: 350.5
Df Model: 3
Covariance Type: nonrobust
==============================================================================coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -21.7176 51.963 -0.418 0.679 -128.529 85.094
lotsize 0.0013 0.001 1.486 0.149 -0.000 0.003
sqrft 0.1170 0.024 4.802 0.000 0.067 0.167
bdrms 25.2012 16.879 1.493 0.147 -9.495 59.897
==============================================================================
Omnibus: 4.958 Durbin-Watson: 1.654
Prob(Omnibus): 0.084 Jarque-Bera (JB): 3.283
Skew: 0.704 Prob(JB): 0.194
Kurtosis: 3.802 Cond. No. 8.78e+04
==============================================================================Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 8.78e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
'''
(二)调用statsmodels的函数进行GQ检验
从statsmodels库的stats子模块的diagnostic工具中导入het_breuschpagan
from statsmodels.stats.diagnostic import het_goldfeldquandt #GQ检验
het_goldfeldquandt函数的参数意义及返回结果
het_goldfeldquandt(y, x, idx=None, split=None, drop=None, alternative='increasing', store=False)
参数意义
y: 被解释变量
x:解释变量
idx: int,按第idx个自变量的大小进行排序
split: 如果split为整数,代表选取前、后各split个组;如果split为0到1之间的小数,选取前、后各int(nobs * split)个组
drop:如果drop为整数,去掉中间drop个组;如果split为0到1之间的小数,选取前、后各int(nobs * drop)个组
alternative:备择假设的形式;原假设是同方差性,若alternative分别为"increasing","decreasing", "two-sided"},代表备择假设分别为具有递增型异方差,递减型异方差,复杂异方差。
store: 默认为False,若为True则返回res_store返回值:
fval : F统计量
pval : F统计量对应的p值
ordering : 备择假设的形式;原假设是同方差性,若alternative分别为"increasing","decreasing", "two-sided"},代表备择假设分别为具有递增型异方差,递减型异方差,复杂异方差。
res_store : ResultsStore, 若参数store为True则返回
formula='price ~ lotsize +sqrft+bdrms',若数据按照第一个自变量lotsize的大小进行排序,选取前后各30组,去掉中间的28组,且查看分组回归结果,则代码如下:
from statsmodels.stats.diagnostic import het_goldfeldquandt #GQ检验
[F,p,order,r]=het_goldfeldquandt(reg.endog,reg.exog,1,30,28,store=True)
print("F=",F)
print("p=",p)
'''
F= 1.658048702954414
p= 0.1020128648382181
'''
若我们需要前30组一元线性回归和后30组一元线性回归结果,则输入代码:
print(r.resols1.summary()) #第一个分组回归结果
print(r.resols2.summary()) #第二个分组回归结果
'''OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.119
Model: OLS Adj. R-squared: 0.017
Method: Least Squares F-statistic: 1.170
Date: Fri, 22 Apr 2022 Prob (F-statistic): 0.340
Time: 14:17:45 Log-Likelihood: -160.84
No. Observations: 30 AIC: 329.7
Df Residuals: 26 BIC: 335.3
Df Model: 3
Covariance Type: nonrobust
==============================================================================coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 94.3425 100.295 0.941 0.356 -111.817 300.502
x1 0.0098 0.010 0.981 0.336 -0.011 0.030
x2 0.0613 0.033 1.844 0.077 -0.007 0.130
x3 -2.0513 15.173 -0.135 0.894 -33.241 29.138
==============================================================================
Omnibus: 19.188 Durbin-Watson: 1.611
Prob(Omnibus): 0.000 Jarque-Bera (JB): 36.110
Skew: 1.299 Prob(JB): 1.44e-08
Kurtosis: 7.705 Cond. No. 5.40e+04
==============================================================================Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 5.4e+04. This might indicate that there are
strong multicollinearity or other numerical problems.OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.720
Model: OLS Adj. R-squared: 0.688
Method: Least Squares F-statistic: 22.30
Date: Fri, 22 Apr 2022 Prob (F-statistic): 2.33e-07
Time: 14:17:45 Log-Likelihood: -168.43
No. Observations: 30 AIC: 344.9
Df Residuals: 26 BIC: 350.5
Df Model: 3
Covariance Type: nonrobust
==============================================================================coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -21.7176 51.963 -0.418 0.679 -128.529 85.094
x1 0.0013 0.001 1.486 0.149 -0.000 0.003
x2 0.1170 0.024 4.802 0.000 0.067 0.167
x3 25.2012 16.879 1.493 0.147 -9.495 59.897
==============================================================================
Omnibus: 4.958 Durbin-Watson: 1.654
Prob(Omnibus): 0.084 Jarque-Bera (JB): 3.283
Skew: 0.704 Prob(JB): 0.194
Kurtosis: 3.802 Cond. No. 8.78e+04
==============================================================================Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 8.78e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
'''
和我们手动编制函数进行GQ检验的回归结果一致。