stata 异方差专题【计量经济系列(四)】
文章目录
- 1. 异方差检验方法
- 2. 散点图法
- 3. BP检验
- 4. 怀特检验
- 5. FWLS 可行权的最小二乘法
- 6. 小练习
ʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞ




“条件异方差”简称异方差,是违背球形扰动假设的一种情形。
1. 异方差检验方法
异方差的检验方法有
①画残差图。
可以是残差与被解释变量的散点图,也可以是残差与某一个解释变量的散点图。
这个方法直观但不严格。
②BP检验。
先建立辅助回归方程,然后进行LM检验或F检验。
在大样本情况下,因为 χ 2 \displaystyle \chi^2 χ2分布 与 F F F分布是等价的,所以使用LM检验和F检验渐进等价。
③怀特检验
BP检验中假设了条件方差函数为线性函数,可能忽略了高次项。怀特检验在BP检验的基础上加入了所有的二次项。
然后进行LM检验或F检验
2. 散点图法
首先,读取数据,并做回归。
use nerlove,clear
quietly reg lntc lnq lnpl lnpk lnpf
绘制 残差 与 拟合值 的散点图。
rvfplot
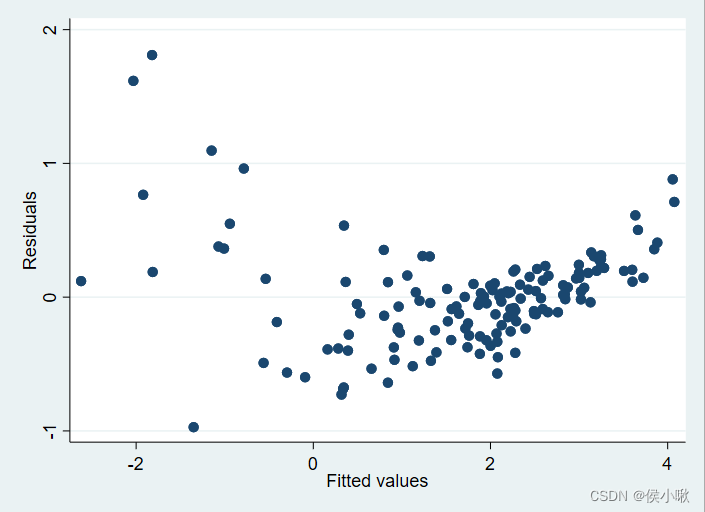
通过图像大致可以看出,拟合值较小时,扰动项较大。
绘制 残差 与 解释变量lnq 的散点图。
rvpplot lnq
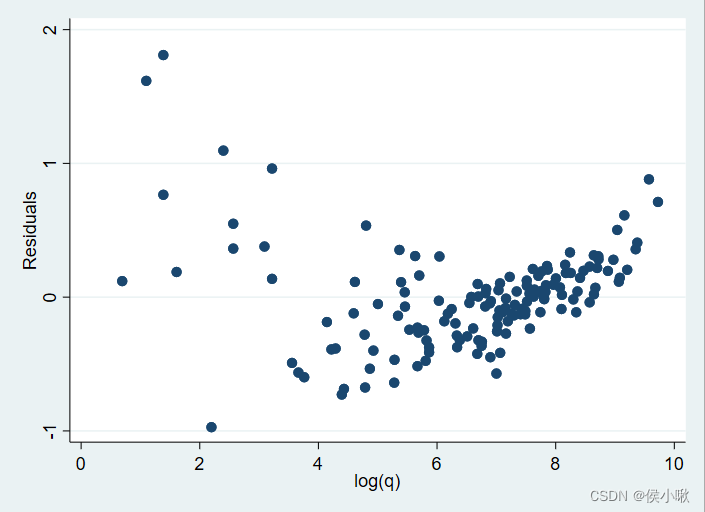
通过图像大致可以看出解释变量lnq越小,扰动项方差越大。
两图都表明扰动项的方差随观测值而改变,即可能存在异方差。
3. BP检验
做BP检验时,可以选择不同的值做辅助回归,比如分别选择拟合值、全部解释变量、部分解释变量做拟合回归。
第一步,读数据,做回归
use nerlove,clear
quietly reg lntc lnq lnpl lnpk lnpf
使用拟合值做辅助回归的BP检验。(默认)
estat hettest,iid

使用所有解释变量做辅助回归的BP检验。(末尾的rhs表示所有解释变量)
estat hettest,iid rhs

使用变量lnq做辅助回归的BP检验。(在estat hettest后边)
estat hettest lnq,iid

BP检验的原假设为,
H 0 : V a r ( ϵ i ∣ x i ) = σ 2 \displaystyle H_0:Var(\epsilon_i|x_i)=\sigma^2 H0:Var(ϵi∣xi)=σ2,表示回归方程“条件同方差”,再通俗地将,也即在不同的x_i上的 许多残差 的方差 之间 也都相等。
经过进一步推导,检验该假设的过程,相当于检验“辅助回归方程不显著”的过程:
三次检验的p值都为0,说明应该拒绝原假设,辅助回归方程显著,
也即 H 0 : V a r ( ϵ i ∣ x i ) = σ 2 \displaystyle H_0:Var(\epsilon_i|x_i)=\sigma^2 H0:Var(ϵi∣xi)=σ2不成立,即存在异方差。
4. 怀特检验
第一步,读数据,做回归
use nerlove,clear
quietly reg lntc lnq lnpl lnpk lnpf
estat imtest,white
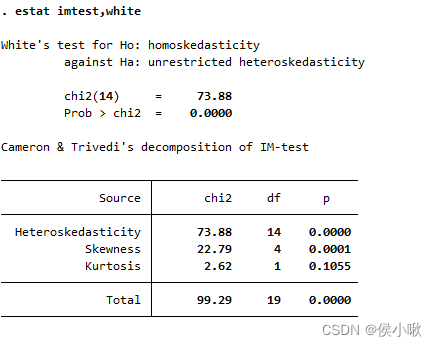
其中imtest指的是信息矩阵检验。
除了在辅助回归中加入了二次项,其他基本同上。如图可见P值为0,表明拒绝原假设,即存在异方差。
5. FWLS 可行权的最小二乘法
WLS事实上不可行,因为权重未知。使用FWLS方法,使用样本数据估计方差,以得到权重 1 v i \displaystyle \frac{1}{\sqrt{v_i}} vi1。其中 v i v_i vi是方差的倒数,也可以表述为是 1 v i \displaystyle \frac{1}{v_i} vi1,这里只是说法不一样,而并非数值不一样。其实运算起来都是一样的。
第一步,读数据,做回归
use nerlove,clear
quietly reg lntc lnq lnpl lnpk lnpf
计算残差(即实际值与拟合值的差),记为变量e1
计算残差平方,记为e2
残差平方取对数,记为lne2
predict e1,residual
gen e2 = e1^2
gen lne2 = log(e2)
对lne2对lnq辅助回归
reg lne2 lnq
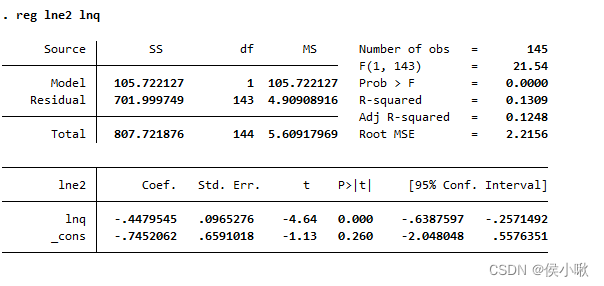
如图可以看出,回归方程在1%的显著性水平下显著,但是 R 2 R^2 R2只有0.1309,且常数项的P值为0.26,常数项不显著。
所以做没有常数项的辅助回归如下:
reg lne2 lnq,noc
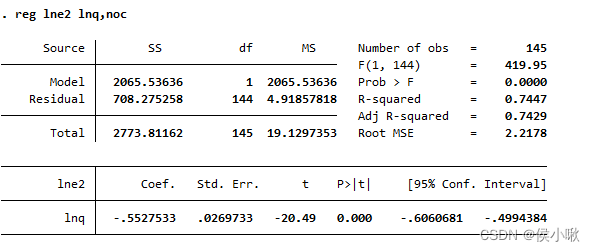
可以看到,无常数项的方程的P值为0,且 R 2 R^2 R2提升为了0.7447。(虽然两个 R 2 R^2 R2之间不可比)
所以用没有常数项的辅助回归效果更佳。
将该辅助回归的拟合值记为lne2f:
再消除对数形式,就得到的方差的估计值
predict lne2f
gen e2f=exp(lne2f)
使用 方差估计值的倒数 作为权重,做WLS回归:
reg lntc lnq lnpl lnpk lnpf[aw=1/e2f]
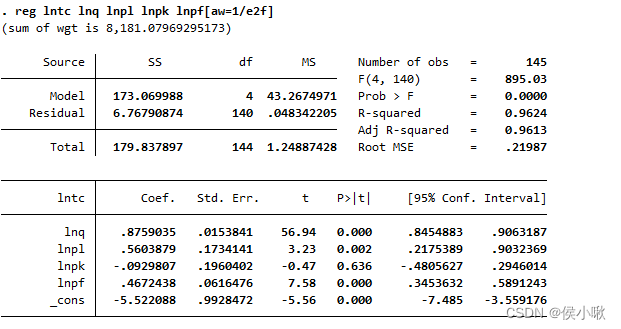
乍一看可能有些复杂,通俗的解释如下:假设是有n个解释变量,一共有m个数据,出现了异方差,则先求出m个数据的每个数据对应的残差,然后求平方,并取对数(如果不取对数做回归则可能会出现该平方形式的变量拟合值为负的情况,而方差不能为负,所以这里一般假设为对数形式),然后用这个新的变量对其中的部分或全部解释变量(比如这里选择的lnq做回归,可能是觉得lnq更具有影响力,且经测试发现无常数项的回归效果更好),做完回归后,求出每个数据位置处的拟合值,则一共会得到m个拟合值。
(这里的 R 2 \displaystyle R^2 R2没多少参考意义。因为衡量的是变换之后的解释变量对变换之后的被解释变量的解释能力。)
至于这里使用的是拟合值,而不是直接使用取完对数的变量,因为取对数之前,lne2只代表残差,而拟合之后,lne2的拟合值才能代表异方差中的方差。将lne2去除对数形式,使用每条数据不尽相同的方差的倒数做回归,可以得到m个权重,给每条数据加权后,就解决了异方差的问题。
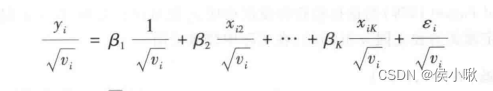
如果担心对条件方差函数的设定不准确,导致加权变换后新的扰动项仍然有一定的异方差,则可以使用稳健标准误进行WLS估计:
即OLS+稳健性标准误
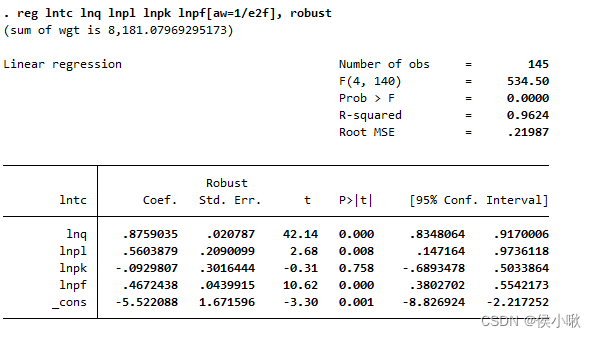
reg lntc lnq lnpl lnpk lnpf[aw=1/e2f], robust
其中robust也可简写为r。
6. 小练习
恩格尔曲线是否存在异方差?
使用数据集 food.dta,其包含有关每周食物开支( food_exp)与每周收入( income)的40个观测值。
use food
(1)将food_exp 与income的散点图与线性拟合图画在一起。根据此图,是否可能存在异方差?此异方差与收入的关系是怎样的?
twoway (scatter food_exp income)(lfit food_exp income)
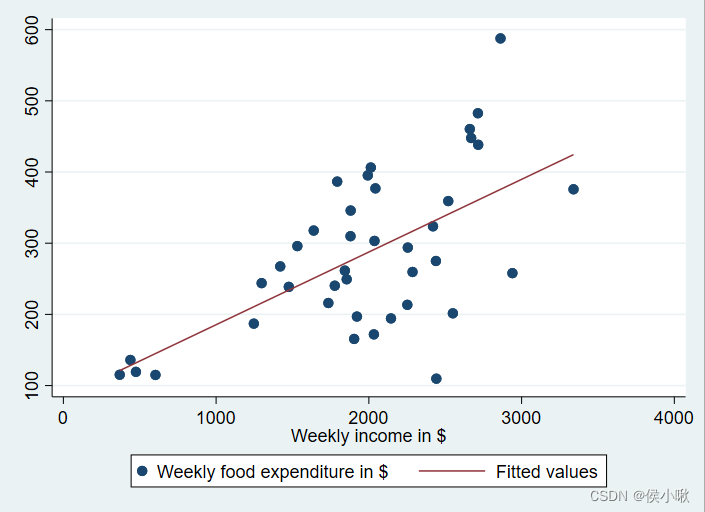
由图可知,可能存在异方差。且解释变量值较小时方差较小,解释变量值较大时方差较大。
(2)将food_exp对income进行回归。
reg food_exp income
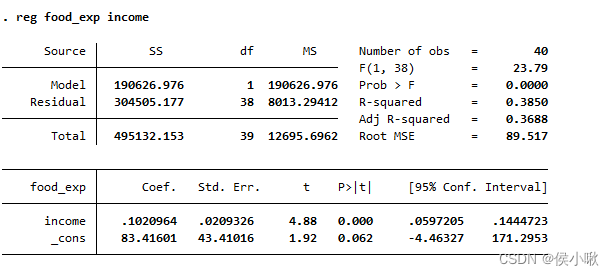
(3)以5%的置信度,使用BP检验,检验是否存在异方差(假设扰动项为iid)。
estat hettest,iid

使用拟合值做辅助回归,P值为0.0066,可以在5%的置信水平下拒绝原假设,即存在异方差。
(4)以5%的置信度,使用怀特检验,检验是否存在异方差。
estat imtest,white
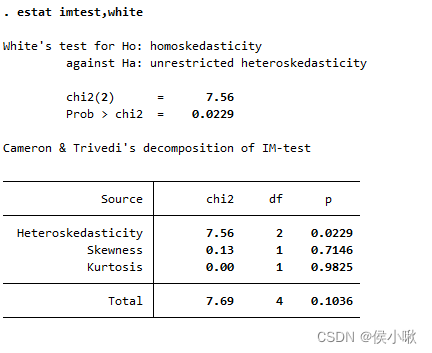
怀特检验P值为0.0229,可以在5%的置信水平下拒绝原假设,即存在异方差。
(5)定义食物开支比例food_share为food_exp除以income ,将 food_share对income做回归,使用散点图法看,是否存在异方差?
生成新变量
gen food_share=food_exp/income
绘制一般散点图和回归直线
twoway (scatter food_share income)(lfit food_share income)
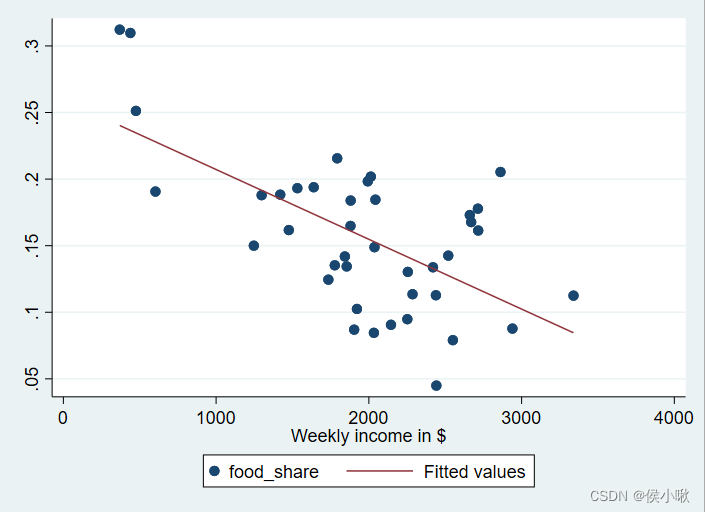
从图形上看并不是太好判断。
绘制残差与拟合值的散点图如下。
quietly reg food_share income
rvfplot
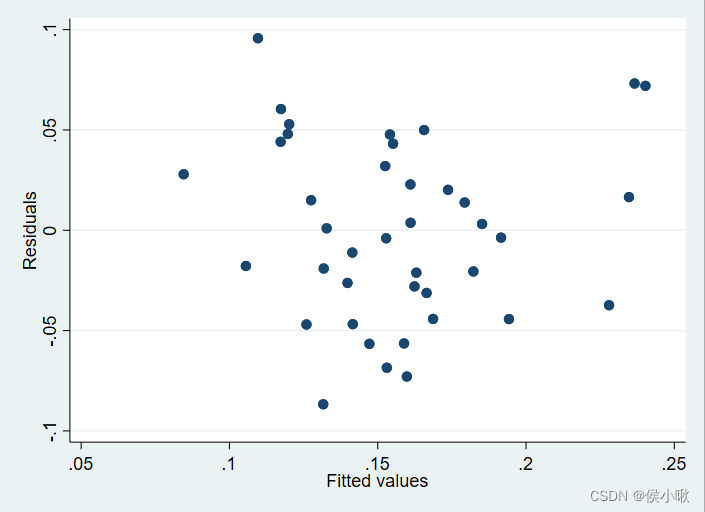
这样的图像不太方便判断是否有异方差,还需进一步检验。
(6)将food_share对income进行回归。
reg food_share income
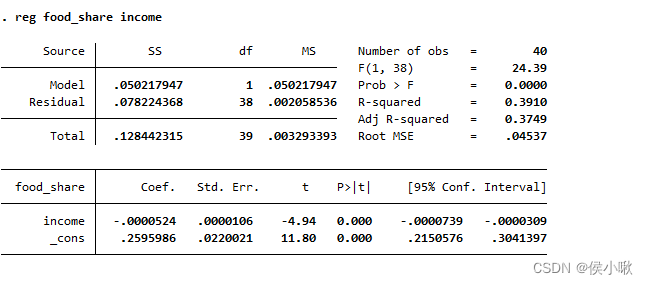
( 7)以5%的置信度,使用BP检验,检验是否存在异方差(假设扰动项为iid )。
estat hettest,iid

P值过大,不能拒绝原假设,说明不存在异方差。
(8)以5%的置信度,使用怀特检验,检验是否存在异方差。
estat imtest,white
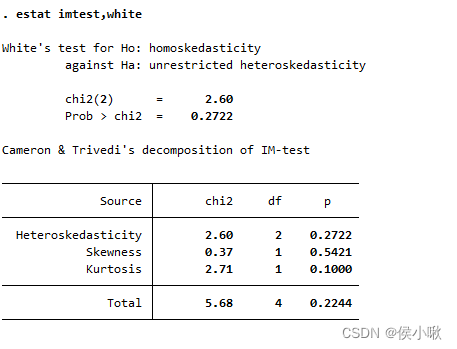
P值过大,不能拒绝原假设,说明不存在异方差。
本次分享就到这里,小啾感谢您的关注与支持!
🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ