一、BCD码

1、BCD码概述

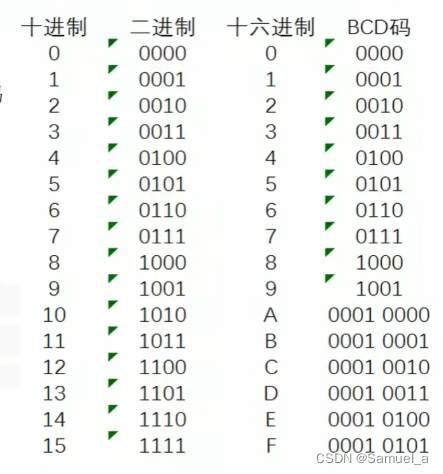
• BCD码（Binary-Coded Decimal‎），用4位二进制数来表示1位十进制数中的0~9这10个数码，是一种二进制的数字编码形式，用二进制编码的十进制代码。BCD码这种编码形式利用了四个位元来储存一个十进制的数码，使二进制和十进制之间的转换得以快捷的进行。
• 相对于一般的浮点式记数法，采用BCD码，既可保存数值的精确度，又可免去使计算机作浮点运算时所耗费的时间。
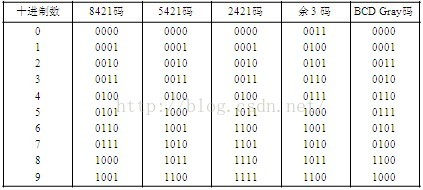
• BCD码也称二进码十进数，BCD码可分为有权码和无权码两类。其中，常见的有权BCD码有8421码、2421码、5421码，无权BCD码有余3码、余3循环码、格雷码。

图片表示

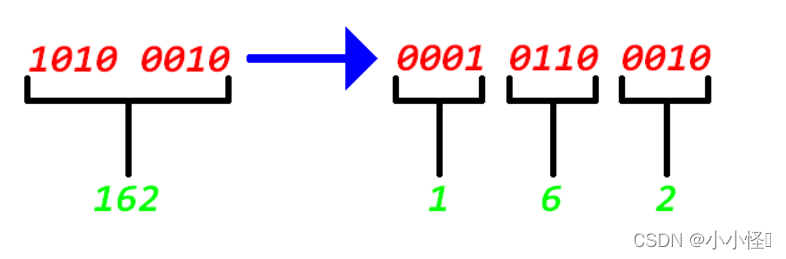
流程详解：
二进制数：1010 0010 = $2^5+2^7+2^1=2+32+128=162$
BCD码是用四位二进制数表示十进制数【0~9】
0001 = $2^0=1$
0110=$2^2+2^1=6$
0010=$2^1=2$

2、BCD分类

BCD码可分为有权码和无权码两类。其中，常见的有权BCD码有8421码、2421码、5421码，无权BCD码有余3码、余3循环码、格雷码。

• 有权码，自然二进制代码是按照二进制代码各位权值大小，以自然向下加一，逢二进一的方式来表示数值的大小所生成的代码。
• 有权码和无权码区别是每一位是否有权值。

1、有权码

8421
8421 BCD码是最基本和最常用的BCD码，它和四位自然二进制码相似，各位的权值为8、4、2、1，故称为有权BCD码。和四位自然二进制码不同的是，它只选用了四位二进制码中前10组代码，即用0000~1001分别代表它所对应的十进制数，余下的六组代码不用。
运算规则：

十进制	0	1	2	3	4	5	6	7	8	9
二进制(BCD8421)	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001
按权相加	0	$2^0$	$2^1$	$2^1+2^0$	$2^2$	$2^2+2^0$	$2^2+2^1$	$2^2+2^1+2^0$	$2^3$	$2^3+2^0$

实例验证：

十进制数：$4+3=7$
二进制数：$0100+0011=0111$

/*二进制加法：逢二进一 */0 1 0 0    4+ 0 0 1 1    30 1 1 1    7

5421

十进制	0	1	2	3	4	5	6	7	8	9
二进制(BCD5421)	0000	0001	0010	0011	0100	1000	1001	1010	1011	1100

2421

十进制	0	1	2	3	4	5	6	7	8	9
二进制(BCD2421)	0000	0001	0010	0011	0100	1011	1100	1101	1110	1111

总结：
有权码就是对应数字为对应位的权值，1代表可以取到该值，0表示取不到。
8421：十进制数：5 二进制数：0101 即4和1能取到$4+1=5$
5421: 十进制数：5 二进制数：1000 即5能取到$5$
2421：十进制数：9 二进制数：1111即2和4和2和1都能取到$2+4+2+1=9$

2、无权码

余三码
余3码是8421 BCD码的每个码组加3(0011)形成的。常用于BCD码的运算电路中。

十进制	0	1	2	3	4	5	6	7	8	9
二进制(BCD余三码)	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100

实例验证：

十进制数：7
二进制数;0111
$2^2+2^1+2^0=4+2+1=7$

/*二进制加法：逢二进一 */0 1 1 1    7+ 0 0 1 1    31 0 1 0   余三码： 7  十进制数：10

余三循环码
余3循环码是无权码，即每个编码中的1和0没有确切的权值，整个编码直接代表一个数值。主要优点是相邻编码只有一位变化，避免了过渡码产生的“噪声”。

十进制	0	1	2	3	4	5	6	7	8	9
二进制(BCD余三循环码)	0010	0110	0111	0101	0100	1100	1101	1111	1110	1010

3、BCD运算问题

我们知道，BCD是用四位二进制数表示十进制数【0~9】的，而四位二进制数可以表示的十进制数为 $2^4=16$ 个即【0~15】，当运算超出范围怎么办？
解决方案：
以$5+8=13$为例
十进制数：$5+8=13$
二进制数：$0101+1000=1101$
差值：$16-10=6$
将所得值加6，产生进位，高位补0
$1101+0110=00010011$

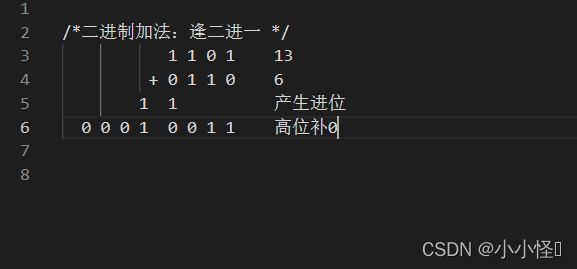
/*二进制加法：逢二进一 */1 1 0 1    13+ 0 1 1 0    61  1          产生进位0 0 0 1  0 0 1 1    高位补0

二、二进制BCD码

1、原理实现

使用逐步移位法来实现二进制数向BCD码的转换；
变量定义：

• B：需要转换的二进制数位宽
• D：转换后的BCD码位宽（其中BCD码的位宽计算如下：根据二进制数的位宽，求出它的无符号数能表示的最大值和最小值，如数据位宽是8位则数据范围大小就是0~255，我们取最大值255，每一个数字对应4位BCD码，三个数字就对应3x4=12位的BCD码）
• N:需要转换的二进制数位宽加上转换后的BCD码位宽

逐步移位法的规则：

• 准备一个N比特的移位寄存器；
• 二进数逐步左移；
• 每次左移之后每个BCD位做大四加三的调整；
• 二进数全部移完，得到结果。

移位流程表

移位次数	BCD[11:8]	BCD[7:4]	BCD[3:0]	bin[7:0]	说明
0				10100101	输入二进制数
1			1	01001010	左移一位，低位补0
2			10	10010100	左移两位，低位补0
3			101	00101000	101=5；大于4加3
3			1000	00101000	加3不移位
4		1	0000	01010000	1000移位，原始值也移位，低位补0
5		10	0000	10100000	循环移位，低位补0
6		100	0001	01000000	循环移位，低位补0
7		1000	0010	10000000	循环移位，低位补0
7		1011	0010	10000000	循环移位，低位补0
8	1	0110	0101	00000000	循环移位，低位补0
BCD	1	6	5		移位结束，输出BCD码

2、模块划分

顶层模块

代码实现

module bin2bcd (input         [7:0]       bin    ,//二进制输入output        [11:0]      bcd     //bcd码输出
);//信号定义wire        [19:0]         bcd_reg0  ;wire        [19:0]         bcd_reg1  ;wire        [19:0]         bcd_reg2  ;wire        [19:0]         bcd_reg3  ;wire        [19:0]         bcd_reg4  ;wire        [19:0]         bcd_reg5  ;wire        [19:0]         bcd_reg6  ;wire        [19:0]         bcd_reg7  ;wire        [19:0]         bcd_reg8  ;//八次移位结果输出assign bcd_reg0 = {12'b0000_0000_0000,bin};//将输入的八位二进制转换为二十位//第一次移位bcd_modify b1(.data_in(bcd_reg0),.data_out(bcd_reg1));//第二次移位bcd_modify b2(.data_in(bcd_reg1),.data_out(bcd_reg2));//第三次移位bcd_modify b3(.data_in(bcd_reg2),.data_out(bcd_reg3));//第四次移位bcd_modify b4(.data_in(bcd_reg3),.data_out(bcd_reg4));//第五次移位bcd_modify b5(.data_in(bcd_reg4),.data_out(bcd_reg5));//第六次移位bcd_modify b6(.data_in(bcd_reg5),.data_out(bcd_reg6));//第七次移位bcd_modify b7(.data_in(bcd_reg6),.data_out(bcd_reg7));//第八次移位bcd_modify b8(.data_in(bcd_reg7),.data_out(bcd_reg8));//BCD输出assign bcd = {bcd_reg8[19:8]};//取高12位为输出结果endmodule

移位模块

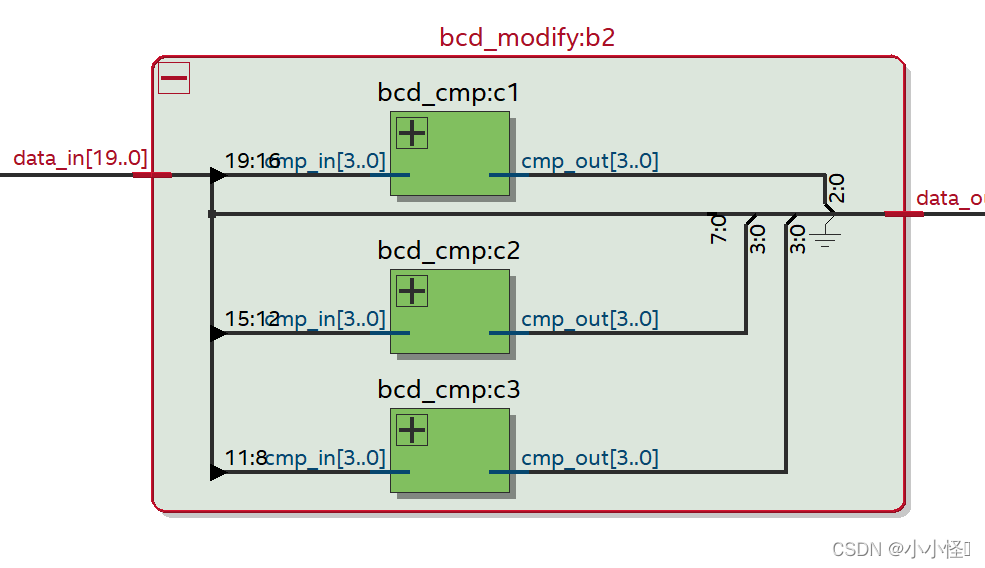
代码实现

//移位处理模块module bcd_modify (input       [19:0]    data_in ,//移位比较数据输入output      [19:0]    data_out //移位比较数据输出
);//信号定义wire         [3:0]      reg1    ;//移位结果输出wire         [3:0]      reg2    ;wire         [3:0]      reg3    ;//左移大4加3比较 [19:16]bcd_cmp c1(.cmp_in(data_in[19:16]),.cmp_out(reg1));//左移大4加3比较 [15:12]bcd_cmp c2(.cmp_in(data_in[15:12]),.cmp_out(reg2));//左移大4加3比较 [11:8]bcd_cmp c3(.cmp_in(data_in[11:8]),.cmp_out(reg3));//比较完成 左移一位assign data_out = {reg1[2:0],reg2,reg3,data_in[7:0],1'b0};endmodule

大四加三处理模块

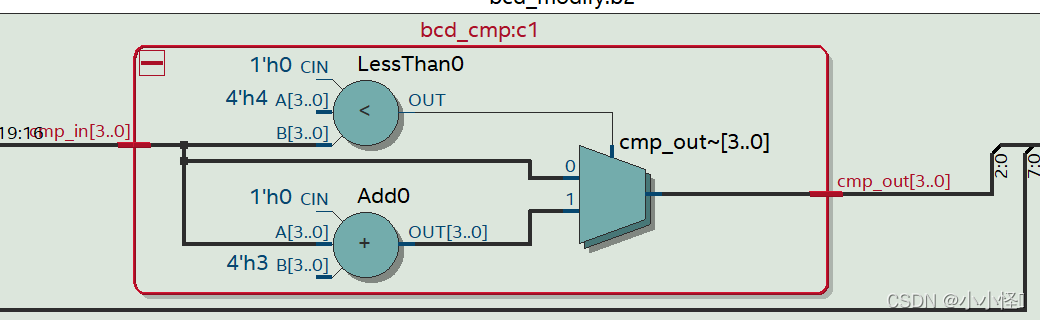
代码实现

//大四加三处理
module bcd_cmp(input      [3:0]    cmp_in  ,//比较器数据输入output  reg[3:0]    cmp_out  //比较器数据输出
);always @(*) beginif(cmp_in > 4)cmp_out = cmp_in + 3;//大于四加三elsecmp_out = cmp_in;//小或等于四 不作处理endendmodule

3、仿真调试

仿真文件【testbench】

`timescale 1ns/1ps
module bin2bcd_tb();
reg        [7:0]     bin   ;
wire       [11:0]    bcd   ;
bin2bcd u_bin2bcd
(.bin         ( bin   ),.bcd         ( bcd   )
);
parameter CYCLE = 20;
initial begin#(CYCLE*200);bin = 8'b0;//bin信号初始化#(CYCLE*100);bin = 8'b1010_1101;//173#(CYCLE*100);bin = 8'b0000_1101;//13#(CYCLE*100);bin = 8'b1010_0100;//164#(CYCLE*100);bin = 8'b1000_0000;//128#(CYCLE*100);bin = 8'b1111_1111;//255$stop;
end
endmodule

【do】文件

vlib work
vmap work work
#编译testbench文件
vlog  bin2bcd_tb.v
#编译设计文件
vlog ../rtl/bcd_cmp.v
vlog ../rtl/bin2bcd.v
vlog ../rtl/bcd_modify.v
#指定仿真顶层
vsim -novopt work.bin2bcd_tb
#添加信号到波形窗
add wave -position insertpoint sim:/bin2bcd_tb//*

do调试流程
打开仿真调试工具modelsim

点击【file】->【change Directory…】

找到tb文件【或者仿真测试文件还有do文件所在目录】

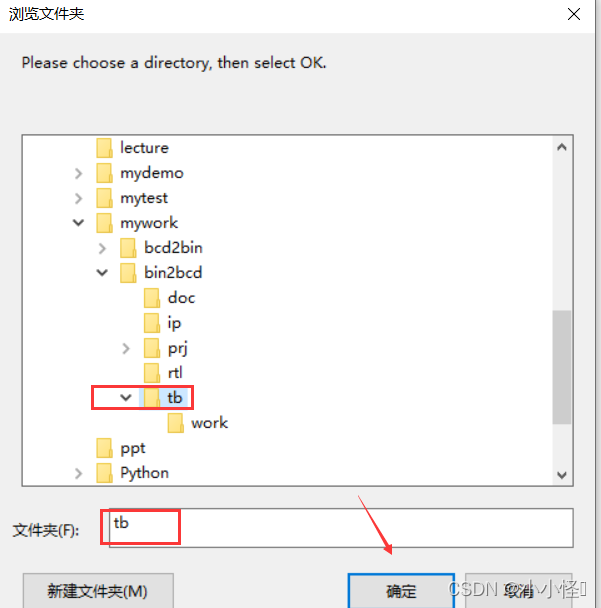
左下角查看打开的目录

使用指令，开始仿真【do do.do】;然后回车

do filename.do

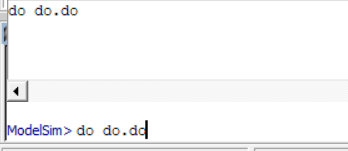
编译无报错【注意错误和警告信息】

4、仿真验证

将bin用十进制表示，加上【unsigned】

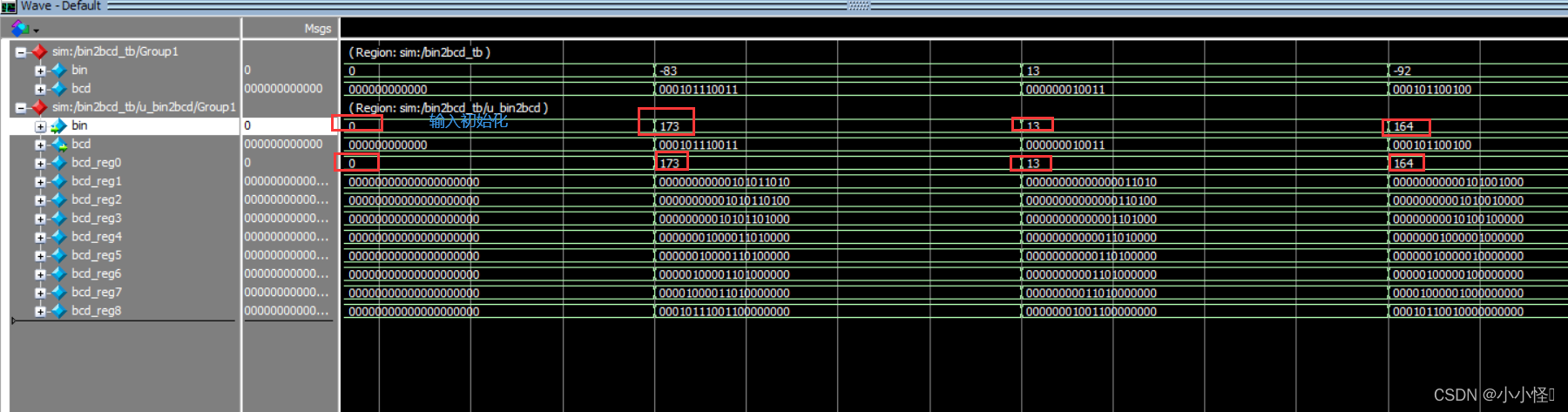
 #(CYCLE*200);bin = 8'b0;//bin信号初始化#(CYCLE*100);bin = 8'b1010_1101;//173#(CYCLE*100);bin = 8'b0000_1101;//13#(CYCLE*100);bin = 8'b1010_0100;//164#(CYCLE*100);bin = 8'b1000_0000;//128#(CYCLE*100);bin = 8'b1111_1111;//255

对比可以发现，输入值符合预期。
下面任意取一个值进行验证。

十进制数：128
BCD码表示：0001 0010 1000

取BCD输出的高12位为输出结果【输入为8，低位为移位补0值】

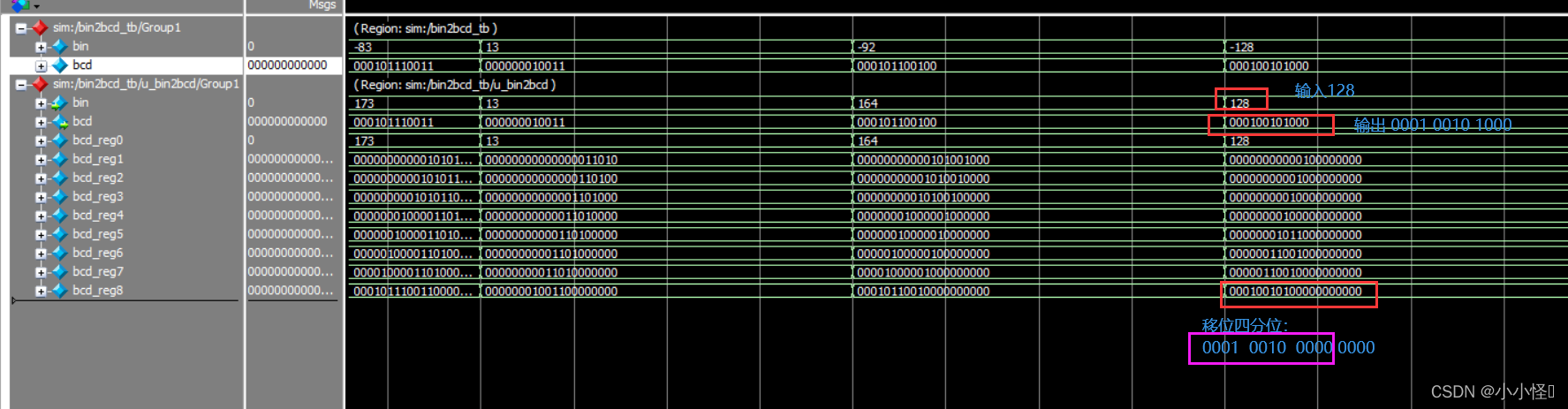
经过对比，输出与实际值吻合。

三、BCD码转二进制

1、原理实现

移位算法原理
二进制码左移一位等于未左移的二进制码*2，例如有二进制码101001，转成十进制等于41，左移一位得到1010010，转成十进制等于82。也就是说二进制码左移1位加上左移3位可以等效于二进制码乘以10。

2、模块划分

移位相加

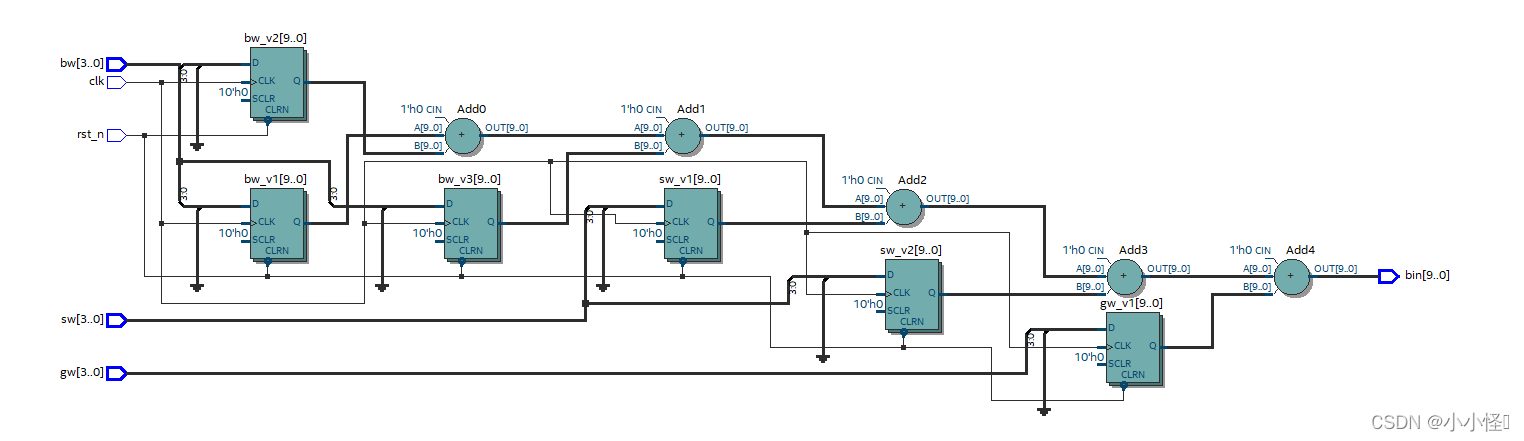
代码实现

/************************工程说明*********************BCD码转二进制码
*****************************************************/
module bcd2bin(input                 clk      ,//系统时钟 50Mhzinput                 rst_n    ,//复位 低电平有效input        [3:0]    bw       ,//BCD码百位input        [3:0]    sw       ,//BCD码十位input        [3:0]    gw       ,//BCD码个位output       [9:0]    bin       //二进制输出
);//信号定义reg           [9:0]    bw_v1   ;//BCD码百位寄存器1reg           [9:0]    bw_v2   ;//BCD码百位寄存器2reg           [9:0]    bw_v3   ;//BCD码百位寄存器3reg           [9:0]    sw_v1   ;//BCD码十位寄存器1reg           [9:0]    sw_v2   ;//BCD码十位寄存器2reg           [9:0]    gw_v1   ;//BCD码个位寄存器/**********************换算规则：**********************BCD百位：a*100=a*(64+32+4)=a*64+a*32+a*4 =a000000+a00000+a00，即a左移6位加上左移5位加上a左移2位 BCD十位：a*10=a*(8+2)=a*8+a*2 =a000+a0，即a左移3位加上左移1位     BCD个位：个位数据不变将所有的各个位的转换结果相加就是转换后的二进制数左移运算：2^n      右移运算：1/(2^n)******************************************************///寄存器赋初值always @(posedge clk or negedge rst_n) beginif(!rst_n)beginbw_v1 <= 0;bw_v2 <= 0;bw_v3 <= 0;sw_v1 <= 0;sw_v2 <= 0;gw_v1 <= 0;endelse beginbw_v1 <= bw << 6;//左移六位bw_v2 <= bw << 5;//左移五位bw_v3 <= bw << 2;//左移两位sw_v1 <= sw << 3;//左移三位sw_v2 <= sw << 1;//左移一位gw_v1 <= gw;//个位保持不变endendassign bin = bw_v1 + bw_v2 + bw_v3 + sw_v1 + sw_v2 + gw_v1;endmodule

3、仿真验证

仿真测试文件【testbench】

//时间单位/精度
`timescale 1ns/1psmodule bcd2bin_tb();
//激励信号
reg                        clk    ;
reg                        rst_n  ;
reg            [3:0]       bw     ;
reg            [3:0]       sw     ;
reg            [3:0]       gw     ;
//输出信号
wire           [9:0]       bin    ;//模块例化
bcd2bin    u_bcd2bin
(.clk       ( clk    ),.rst_n     ( rst_n  ),.bw        ( bw     ),.gw        ( gw     ),.sw        ( sw     ),.bin       ( bin    )
);//产生时钟
parameter CYCLE = 20;always #(CYCLE/2) clk = ~clk;//产生激励initial beginclk   = 1'b0;rst_n = 1'b0;bw = 4'd0; sw = 4'd0; gw = 4'd0;//000#(CYCLE*500);rst_n = 1'b1;#(CYCLE*1000);bw = 4'd1; sw = 4'd2; gw = 4'd0;//120#(CYCLE*1000);bw = 4'd3; sw = 4'd2; gw = 4'd9;//329#(CYCLE*1000);bw = 4'd7; sw = 4'd0; gw = 4'd3;//703#(CYCLE*1000);bw = 4'd0; sw = 4'd2; gw = 4'd7;//027#(CYCLE*1000);bw = 4'd2; sw = 4'd9; gw = 4'd0;//290#(CYCLE*5000);$stop;endendmodule

do文件

vlib work
vmap work work#编译testbench文件
vlog bcd2bin_tb.v#编译设计文件 
vlog ../rtl/bcd2bin.v#指定仿真顶层
vsim -novopt work.bcd2bin_tb#添加信号到波形窗
add wave -position insertpoint sim:/bcd2bin_tb//*

验证结果
输入值查看

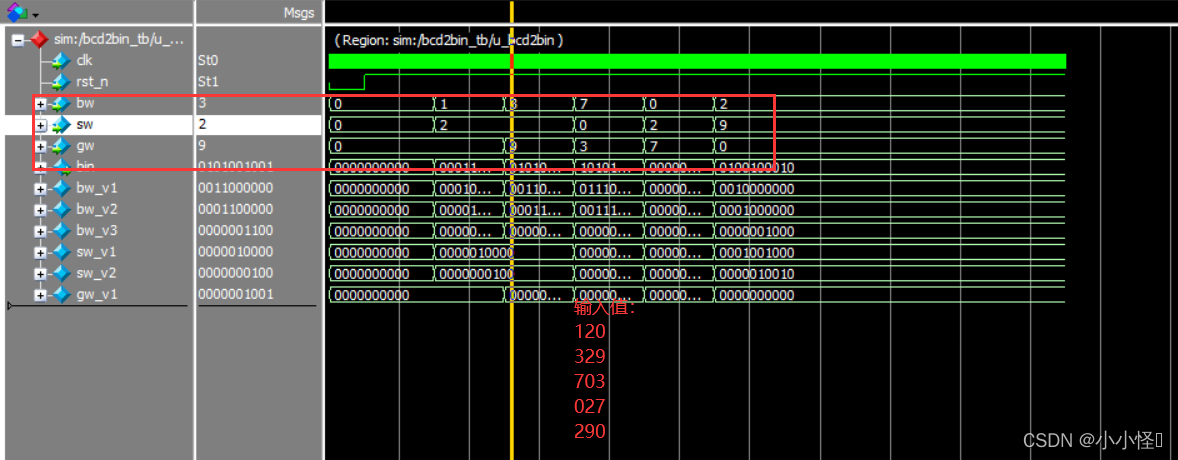
仿真输入值

bw = 4'd0; sw = 4'd0; gw = 4'd0;//000#(CYCLE*500);rst_n = 1'b1;#(CYCLE*1000);bw = 4'd1; sw = 4'd2; gw = 4'd0;//120#(CYCLE*1000);bw = 4'd3; sw = 4'd2; gw = 4'd9;//329#(CYCLE*1000);bw = 4'd7; sw = 4'd0; gw = 4'd3;//703#(CYCLE*1000);bw = 4'd0; sw = 4'd2; gw = 4'd7;//027#(CYCLE*1000);bw = 4'd2; sw = 4'd9; gw = 4'd0;//290#(CYCLE*5000);

输出结果

百位：左移六位+左移五位+左移两位
十位：左移三位+左移一位
个位：不变

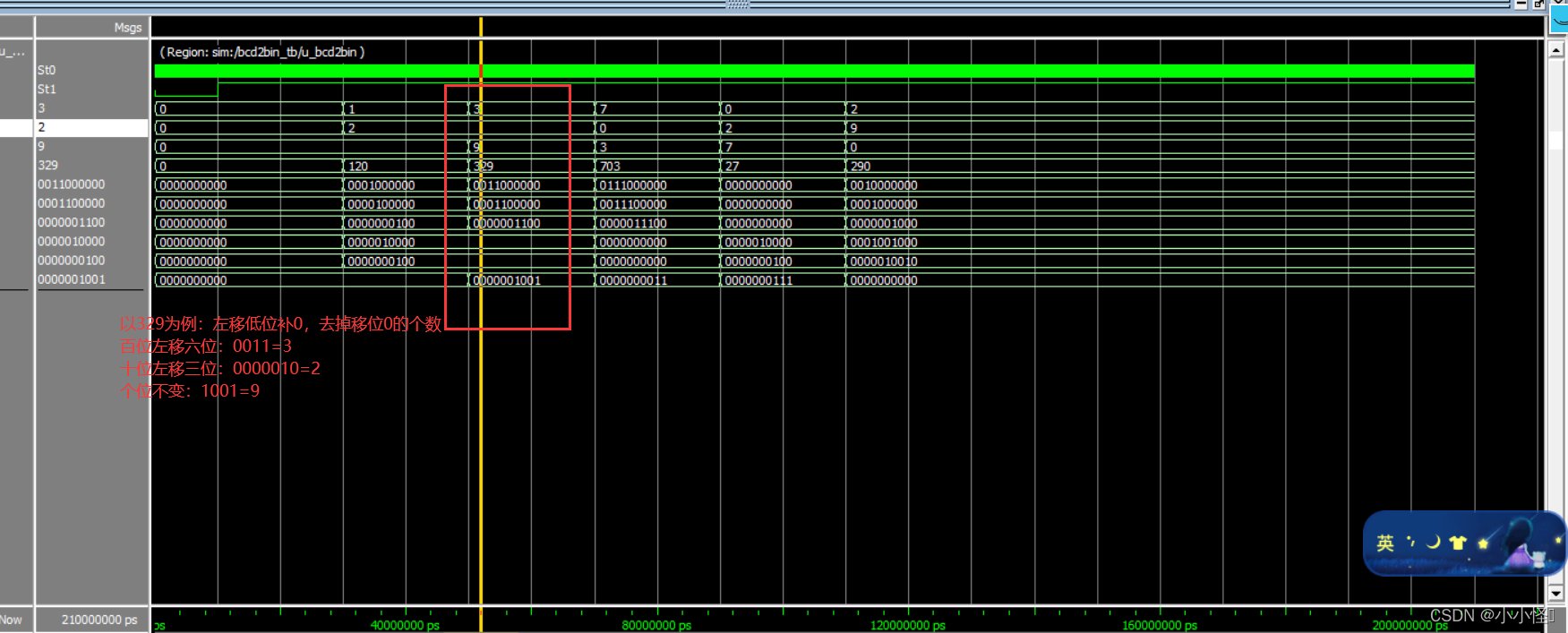
经对比，结果符合预期。