BLAS之GEMM和GEMV

article/2025/9/17 23:43:27

BLAS简介

BLAS全称是Basic Linear Algebra Subprograms是规定了一套低级的执行常见线性代数操作的规范。其实现经常针对特殊的机器进行优化，比较著名的·BLAS库有ACML, ATLAS, MKL, OpenBLAS。许多常见的数值软件均采用兼容BLAS规范的实现库来进行线性代数计算，比如Matlab, Numpy, Mathematica`。

其中，Level 1 BLAS主要提供向量操作


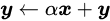
Level 2 BLAS提供矩阵向量操作（gemv)

gemv


而Level 3 BLAS则提供广义矩阵乘积操作(gemm)

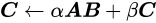
gemm


GEMM在深度学习中是十分重要的，全连接层以及卷积层基本上都是通过GEMM来实现的，而网络中大约90%的运算都是在这两层中。而一个良好的GEMM的实现可以充分利用系统的多级存储结构和程序执行的局部性来充分加速运算。

 

gemm接口解析

gemm的函数接口如下图所示，darknet中也采用了类似的接口设计。

sgemm
其中，A,B,C分别是MxK, KxN, MxN的矩阵，TRANSA, TRANSB, TRANSC表示是否使用对应矩阵的转置，ALPHA, BETA为对应的系数。而LDA, LDB, LDC表示对应矩阵的leading dimension，即第一维度的大小。根据我的理解（结合darknet的源码），是因为在内存中是连续存放的，而这个leading dimension的量是用来定义元素的位置的，即add(A[i, j])=A+i*lda+j。其中sgemm中的s表示是单精度的运算，类似的，还有dgemm。

gemm代码分析：


源码

 **  -- Reference BLAS level3 routine (version 3.7.0) --*  -- Reference BLAS is a software package provided by Univ. of Tennessee,    --*  -- Univ. of California Berkeley, Univ. of Colorado Denver and NAG Ltd..--*     December 2016**     .. Scalar Arguments ..REAL ALPHA,BETAINTEGER K,LDA,LDB,LDC,M,NCHARACTER TRANSA,TRANSB*     ..*     .. Array Arguments ..REAL A(LDA,*),B(LDB,*),C(LDC,*)*     ..**  =====================================================================**     .. External Functions ..LOGICAL LSAMEEXTERNAL lsame*     ..*     .. External Subroutines ..EXTERNAL xerbla*     ..*     .. Intrinsic Functions ..INTRINSIC max*     ..*     .. Local Scalars ..REAL TEMPINTEGER I,INFO,J,L,NCOLA,NROWA,NROWBLOGICAL NOTA,NOTB*     ..*     .. Parameters ..REAL ONE,ZEROparameter(one=1.0e+0,zero=0.0e+0)*     ..**     Set  NOTA  and  NOTB  as  true if  A  and  B  respectively are not*     transposed and set  NROWA, NCOLA and  NROWB  as the number of rows*     and  columns of  A  and the  number of  rows  of  B  respectively.*nota = lsame(transa,'N')notb = lsame(transb,'N')IF (nota) THENnrowa = mncola = kELSEnrowa = kncola = mEND IFIF (notb) THENnrowb = kELSEnrowb = nEND IF**     Test the input parameters.*info = 0IF ((.NOT.nota) .AND. (.NOT.lsame(transa,'C')) .AND.+    (.NOT.lsame(transa,'T'))) THENinfo = 1ELSE IF ((.NOT.notb) .AND. (.NOT.lsame(transb,'C')) .AND.+         (.NOT.lsame(transb,'T'))) THENinfo = 2ELSE IF (m.LT.0) THENinfo = 3ELSE IF (n.LT.0) THENinfo = 4ELSE IF (k.LT.0) THENinfo = 5ELSE IF (lda.LT.max(1,nrowa)) THENinfo = 8ELSE IF (ldb.LT.max(1,nrowb)) THENinfo = 10ELSE IF (ldc.LT.max(1,m)) THENinfo = 13END IFIF (info.NE.0) THENCALL xerbla('SGEMM ',info)RETURNEND IF**     Quick return if possible.*IF ((m.EQ.0) .OR. (n.EQ.0) .OR.+    (((alpha.EQ.zero).OR. (k.EQ.0)).AND. (beta.EQ.one))) RETURN**     And if  alpha.eq.zero.*IF (alpha.EQ.zero) THENIF (beta.EQ.zero) THENDO 20 j = 1,nDO 10 i = 1,mc(i,j) = zero10             CONTINUE20         CONTINUEELSEDO 40 j = 1,nDO 30 i = 1,mc(i,j) = beta*c(i,j)30             CONTINUE40         CONTINUEEND IFRETURNEND IF**     Start the operations.*IF (notb) THENIF (nota) THEN**           Form  C := alpha*A*B + beta*C.*DO 90 j = 1,nIF (beta.EQ.zero) THENDO 50 i = 1,mc(i,j) = zero50                 CONTINUEELSE IF (beta.NE.one) THENDO 60 i = 1,mc(i,j) = beta*c(i,j)60                 CONTINUEEND IFDO 80 l = 1,ktemp = alpha*b(l,j)DO 70 i = 1,mc(i,j) = c(i,j) + temp*a(i,l)70                 CONTINUE80             CONTINUE90         CONTINUEELSE**           Form  C := alpha*A**T*B + beta*C*DO 120 j = 1,nDO 110 i = 1,mtemp = zeroDO 100 l = 1,ktemp = temp + a(l,i)*b(l,j)100                 CONTINUEIF (beta.EQ.zero) THENc(i,j) = alpha*tempELSEc(i,j) = alpha*temp + beta*c(i,j)END IF110             CONTINUE120         CONTINUEEND IFELSEIF (nota) THEN**           Form  C := alpha*A*B**T + beta*C*DO 170 j = 1,nIF (beta.EQ.zero) THENDO 130 i = 1,mc(i,j) = zero130                 CONTINUEELSE IF (beta.NE.one) THENDO 140 i = 1,mc(i,j) = beta*c(i,j)140                 CONTINUEEND IFDO 160 l = 1,ktemp = alpha*b(j,l)DO 150 i = 1,mc(i,j) = c(i,j) + temp*a(i,l)150                 CONTINUE160             CONTINUE170         CONTINUEELSE**           Form  C := alpha*A**T*B**T + beta*C*DO 200 j = 1,nDO 190 i = 1,mtemp = zeroDO 180 l = 1,ktemp = temp + a(l,i)*b(j,l)180                 CONTINUEIF (beta.EQ.zero) THENc(i,j) = alpha*tempELSEc(i,j) = alpha*temp + beta*c(i,j)END IF190             CONTINUE200         CONTINUEEND IFEND IF*RETURN**     End of SGEMM .*

 SGEMV  performs one of the matrix-vector operationsy := alpha*A*x + beta*y,   or   y := alpha*A**T*x + beta*y,where alpha and beta are scalars, x and y are vectors and A is anm by n matrix.

源码： 

 **  -- Reference BLAS level2 routine (version 3.7.0) --*  -- Reference BLAS is a software package provided by Univ. of Tennessee,    --*  -- Univ. of California Berkeley, Univ. of Colorado Denver and NAG Ltd..--*     December 2016**     .. Scalar Arguments ..REAL ALPHA,BETAINTEGER INCX,INCY,LDA,M,NCHARACTER TRANS*     ..*     .. Array Arguments ..REAL A(LDA,*),X(*),Y(*)*     ..**  =====================================================================**     .. Parameters ..REAL ONE,ZEROparameter(one=1.0e+0,zero=0.0e+0)*     ..*     .. Local Scalars ..REAL TEMPINTEGER I,INFO,IX,IY,J,JX,JY,KX,KY,LENX,LENY*     ..*     .. External Functions ..LOGICAL LSAMEEXTERNAL lsame*     ..*     .. External Subroutines ..EXTERNAL xerbla*     ..*     .. Intrinsic Functions ..INTRINSIC max*     ..**     Test the input parameters.*info = 0IF (.NOT.lsame(trans,'N') .AND. .NOT.lsame(trans,'T') .AND.+    .NOT.lsame(trans,'C')) THENinfo = 1ELSE IF (m.LT.0) THENinfo = 2ELSE IF (n.LT.0) THENinfo = 3ELSE IF (lda.LT.max(1,m)) THENinfo = 6ELSE IF (incx.EQ.0) THENinfo = 8ELSE IF (incy.EQ.0) THENinfo = 11END IFIF (info.NE.0) THENCALL xerbla('SGEMV ',info)RETURNEND IF**     Quick return if possible.*IF ((m.EQ.0) .OR. (n.EQ.0) .OR.+    ((alpha.EQ.zero).AND. (beta.EQ.one))) RETURN**     Set  LENX  and  LENY, the lengths of the vectors x and y, and set*     up the start points in  X  and  Y.*IF (lsame(trans,'N')) THENlenx = nleny = mELSElenx = mleny = nEND IFIF (incx.GT.0) THENkx = 1ELSEkx = 1 - (lenx-1)*incxEND IFIF (incy.GT.0) THENky = 1ELSEky = 1 - (leny-1)*incyEND IF**     Start the operations. In this version the elements of A are*     accessed sequentially with one pass through A.**     First form  y := beta*y.*IF (beta.NE.one) THENIF (incy.EQ.1) THENIF (beta.EQ.zero) THENDO 10 i = 1,lenyy(i) = zero10             CONTINUEELSEDO 20 i = 1,lenyy(i) = beta*y(i)20             CONTINUEEND IFELSEiy = kyIF (beta.EQ.zero) THENDO 30 i = 1,lenyy(iy) = zeroiy = iy + incy30             CONTINUEELSEDO 40 i = 1,lenyy(iy) = beta*y(iy)iy = iy + incy40             CONTINUEEND IFEND IFEND IFIF (alpha.EQ.zero) RETURNIF (lsame(trans,'N')) THEN**        Form  y := alpha*A*x + y.*jx = kxIF (incy.EQ.1) THENDO 60 j = 1,ntemp = alpha*x(jx)DO 50 i = 1,my(i) = y(i) + temp*a(i,j)50             CONTINUEjx = jx + incx60         CONTINUEELSEDO 80 j = 1,ntemp = alpha*x(jx)iy = kyDO 70 i = 1,my(iy) = y(iy) + temp*a(i,j)iy = iy + incy70             CONTINUEjx = jx + incx80         CONTINUEEND IFELSE**        Form  y := alpha*A**T*x + y.*jy = kyIF (incx.EQ.1) THENDO 100 j = 1,ntemp = zeroDO 90 i = 1,mtemp = temp + a(i,j)*x(i)90             CONTINUEy(jy) = y(jy) + alpha*tempjy = jy + incy100         CONTINUEELSEDO 120 j = 1,ntemp = zeroix = kxDO 110 i = 1,mtemp = temp + a(i,j)*x(ix)ix = ix + incx110             CONTINUEy(jy) = y(jy) + alpha*tempjy = jy + incy120         CONTINUEEND IFEND IF*RETURN**     End of SGEMV .*

 

 

 

参考文献

  1. Basic Linear Algebra Subprograms-WikiPeia
  2. Dongarra J J, Croz J D, Hammarling S, et al. A set of level 3 basic linear algebra subprograms[J]. Acm Transactions on Mathematical Software, 1990, 16(1):1-17.
  3. Why gemm is at the heart of deep learning
  4. sgemm 官方文档
  5. https://www.jianshu.com/p/1dd118f431eb

http://chatgpt.dhexx.cn/article/VjE15nv4.shtml

相关文章

linux编译blas,科学网—Linux下安装blas和lapack包小记 - 徐博伦的博文

linux编译blas,科学网—Linux下安装blas和lapack包小记 - 徐博伦的博文

系统是centOS6.5，机器上已有gfortran编译器 从网上搜索下载blas、cblas、lapack的tar压缩文件包 1.编译blas 先解压文件 tar xvf blas.tgz cd blas #blas的解压文件夹 gfortran -c -O3 *.f #编译生成.o执行文件 ar rv libblas.a *.o #链接所有的 .o文件&#xff0…
阅读更多...
BLAS学习

BLAS学习

导师突然通知要开始关于blas的讨论班，之前甚至都没听说过blas这个词，又要开始新一波的锤炼小白之路了… 1. BLAS简介 首先BLAS的全称是 Basic Linear Algebra Subprograms，即 基础线性代数子程序库，其中包含了一系列基本的线性代…
阅读更多...
android 您的手机上未安装应用程序的解决方法

android 您的手机上未安装应用程序的解决方法

android 创建桌面快捷方式的时候设置应用名称和图标是完全没有问题，但是点击快捷方式的时候出现“您的手机上未安装应用程序“，这是快捷方式的执行目标设置错误，也就是启动Activity。有些应用的启动Activity是欢迎界面，创建快捷方…
阅读更多...
android显示应用程序未安装,如何解决安卓系统显示应用程序未安装

android显示应用程序未安装,如何解决安卓系统显示应用程序未安装

我们在安装软件的时候经常会遇到应用程序未安装这个问题，尤其是在更新软件或者是从ROM提取出来的软件会出现这样的问题。那我们该如何处理这个问题呢？下面我就为大家列举几个解决这种问题的办法。 产生应用程序未安装的原因 软件签名不一致。这种情况一般…
阅读更多...
什么是android应用程序未安装,应用程序未安装,教您安卓系统应用程序未安装怎么解决...

什么是android应用程序未安装,应用程序未安装,教您安卓系统应用程序未安装怎么解决...

大家在使用智能手机的时候，尤其是安卓系统的手机，在安装应用程序，也就是App的时候，有时会提示“应用程序未安装”，相信很多使用安卓机器的朋友都曾遇到过“应用程序未安装”的问题，但是懂得解决的用户并不多…
阅读更多...
android studio AVD模拟器安装某些app出现 “app not installed(未安装应用程序)”的问题

android studio AVD模拟器安装某些app出现 “app not installed(未安装应用程序)”的问题

android studio AVD模拟器安装某些app出现 “app not installed(未安装应用程序)”的问题 参考： 安装apk时出现INSTALL_FAILED_NO_MATCHING_ABIS？Android 开发之 INSTALL_FAILED 汇集表 问题说明 在为安卓模拟器中android 11版本的系统安装一些常用软…
阅读更多...
一加5应用未安装怎么解决_应用程序未安装怎么解决 手机提示应用程序未安装解决办法...

一加5应用未安装怎么解决_应用程序未安装怎么解决 手机提示应用程序未安装解决办法...

安卓手机系统的应用繁多，丰富人们使用体验的同时，有时候还会出现种种问题，比如安装提示“应用程序未安装”，那么，遇见这个问题应该怎么处理呢？请阅读本文教程！ 手机提示应用程序未安装解决办法 …
阅读更多...
android开发下载安装app提示未安装应用

android开发下载安装app提示未安装应用

出现的情况是通过usb可以安装，然后用androidStudio运行生成的apk,发送出去，下载安装，提示未安装应用: 问题如图: 解决过程:在百度上看一些方案,不一致呢,问了问别人,通过正确的打包方式打包试一下,尝试过在AndroidStudio通过Build,然后Build…
阅读更多...
什么是android应用程序未安装,显示“应用程序未安装”是怎么回事？程序未安装的解决图文步骤...

什么是android应用程序未安装,显示“应用程序未安装”是怎么回事？程序未安装的解决图文步骤...

安卓手机安装应用的时候，有时候会莫名其妙无法安装……明明存储空间够的啊摔!经过搜索和尝试，本人找到一种可行的方法，下面分享给大家。目前看来，这是部分系统内的bug，下面，小编跟大家介绍安卓系统应用程序…
阅读更多...
Andorid手机安装apk文件，提示应用未安装

Andorid手机安装apk文件，提示应用未安装

项目场景：Andorid手机安装apk文件，提示应用未安装 通过Andorid studio打包生成的apk文件，在Andorid手机上安装时，提示应用未安装 安装apk文件到手机上，提示“应用未安装” 原因分析： 可能是手机上的Andor…
阅读更多...
安装APK时提示“应用未安装”

安装APK时提示“应用未安装”

情况说明：最近在做公司的移动端项目，作为新手碰到许多问题，不过也算是在披荆斩棘般前行。本来今天星期一高高兴兴来上班，结果测试姐姐跑过来说应用程序安装不上，忙活了一上午也没什么结果，最后还是靠公司前…
阅读更多...
应用未安装

应用未安装

安卓删除软件之后安装失败 我在使用uniapp开发玩一个软件之后，打包，由于安卓之前是有一个旧的版本的，于是我把旧的版本删除之后，再去安装新的包，就会一直报错。 如图所示 出现这种原因是因为我在删除的时候&#xff…
阅读更多...
手机apk应用程序未安装解决办法

手机apk应用程序未安装解决办法

用智能手机很多都会遇到“X应用程序未安装”这种情况，这是为什么呢？1、软件未卸载干净，比如是我以前手机装过手机淘宝，非正常卸载后再装可能就提示X应用程序未安装；2、下载的安装包不完整，也会导致X应用程序…
阅读更多...
89C51单片机中的中断系统

89C51单片机中的中断系统

89C51单片机中的中断系统 对于在单片机中的学习，中断系统是一难点，如果中断系统没有理解透彻，51单片机的学习就算是失败的。 首先，举例说明下什么是中断。 eg.当你在家正在吃着爆米花，看着电视，突然门铃响…
阅读更多...
AT89C51单片机交通灯仿真图+代码

AT89C51单片机交通灯仿真图+代码

接上篇万年历，这篇博客也是记录我的实训内容，我们实训有万年历和交通灯。好了不说闲话，上正文。 不知道为何突然发现说原创审核不过，完全手写的，也不知道为何，哭 注：在评论有附本人交通灯的图噢…
阅读更多...
基于AT89C51单片机的电子万年历PROTEUS仿真设计

基于AT89C51单片机的电子万年历PROTEUS仿真设计

目录 前 言 1 第一章 工作原理 2 1.1设计目标 2 1.1.1基本功能 2 第二章 硬件设计与原理 3 2.1 总设计框图 3 2.2 硬件设计分析 3 2.2.1 电源的设计 3 2.2.2 单片机最小系统 4 2.2.3 显示系统 10 2.2.4 LCD1602的指令说明及时序 12 2.2.5 LCD1602的RAM地址映射及标准字库表 14 …
阅读更多...
基于at89c51单片机的交通灯控制设计

基于at89c51单片机的交通灯控制设计

** 单片机自主学习项目*设计分析 —模拟LED交通灯 ** 一、开发背景与需求 1 开发背景 交通事业蓬勃发展，交通流量年年增长，道路交通繁忙，经常有严重堵车现象，特别是在交叉口，为了在叉口的各条干道实现合理的科学分…
阅读更多...
以梦为马之89c51单片机驱动lcd

以梦为马之89c51单片机驱动lcd

路有千万条，我要选择那条最难的走，这才是我该走的路 控制LCD实际上就是控制两个牛屎芯片 观察lcd1602，它有16个引脚，其含义如下图所示 查看数据手册看到如下时序图 再看说明书看到时序图介绍： 芯片手册混合写的&a…
阅读更多...
AT89C51单片机的C语言代码和仿真模拟学习

AT89C51单片机的C语言代码和仿真模拟学习

单片机定时器学习 一、代码图片与仿真模拟图 #include <reg51.h>/*定义KEY*/ sbit KEY1 P1^0; sbit KEY2 P1^1;void Delay100ms() //12.000MHz延时100ms {unsigned char i, j;i 195;j 138;do{while (--j);} while (--i); }//判断KEY值并执行程序 void Judgefunctio…
阅读更多...
AT89C51单片机制作简易密码锁

AT89C51单片机制作简易密码锁

51单片机课程设计—制作密码锁 文章目录 51单片机课程设计---制作密码锁1.设计要求2.设计流程图3.重要代码解释4.仿真电路设计5.完整代码设计6.仿真结果图7.工程源码及protues仿真下载 1.设计要求 1.1能设定一组4位的数字开启密码&#xff08;设定密码功能&#xff09; 1.2用L…
阅读更多...
推荐文章

Copyright @ 2022~2023