0. 前言

本文翻译自博客： iamtrask.github.io ，这次翻译已经获得trask本人的同意与支持，在此特别感谢trask。本文属于作者一边学习一边翻译的作品，所以在用词、理论方面难免会出现很多错误，假如您发现错误或者不合适的地方，可以给我留言，谢谢！

--- 2016.7.26 UPDATE ---

不涉及商业用途无须告知本人即可转载，但请注明出处！

原文地址：blog.csdn.net/zzukun/article/details/49968129

---

1. 概要

我的最佳学习法就是通过玩具代码，一边调试一边学习理论。这篇博客通过一个非常简单的python玩具代码来讲解循环神经网络。

那么依旧是废话少说，放‘码’过来！

import copy, numpy as np
np.random.seed(0)# compute sigmoid nonlinearity
def sigmoid(x):output = 1/(1+np.exp(-x))return output# convert output of sigmoid function to its derivative
def sigmoid_output_to_derivative(output):return output*(1-output)# training dataset generation
int2binary = {}
binary_dim = 8largest_number = pow(2,binary_dim)
binary = np.unpackbits(np.array([range(largest_number)],dtype=np.uint8).T,axis=1)
for i in range(largest_number):int2binary[i] = binary[i]# input variables
alpha = 0.1
input_dim = 2
hidden_dim = 16
output_dim = 1# initialize neural network weights
synapse_0 = 2*np.random.random((input_dim,hidden_dim)) - 1
synapse_1 = 2*np.random.random((hidden_dim,output_dim)) - 1
synapse_h = 2*np.random.random((hidden_dim,hidden_dim)) - 1synapse_0_update = np.zeros_like(synapse_0)
synapse_1_update = np.zeros_like(synapse_1)
synapse_h_update = np.zeros_like(synapse_h)# training logic
for j in range(10000):# generate a simple addition problem (a + b = c)a_int = np.random.randint(largest_number/2) # int versiona = int2binary[a_int] # binary encodingb_int = np.random.randint(largest_number/2) # int versionb = int2binary[b_int] # binary encoding# true answerc_int = a_int + b_intc = int2binary[c_int]# where we'll store our best guess (binary encoded)d = np.zeros_like(c)overallError = 0layer_2_deltas = list()layer_1_values = list()layer_1_values.append(np.zeros(hidden_dim))# moving along the positions in the binary encodingfor position in range(binary_dim):# generate input and outputX = np.array([[a[binary_dim - position - 1],b[binary_dim - position - 1]]])y = np.array([[c[binary_dim - position - 1]]]).T# hidden layer (input ~+ prev_hidden)layer_1 = sigmoid(np.dot(X,synapse_0) + np.dot(layer_1_values[-1],synapse_h))# output layer (new binary representation)layer_2 = sigmoid(np.dot(layer_1,synapse_1))# did we miss?... if so by how much?layer_2_error = y - layer_2layer_2_deltas.append((layer_2_error)*sigmoid_output_to_derivative(layer_2))overallError += np.abs(layer_2_error[0])# decode estimate so we can print it outd[binary_dim - position - 1] = np.round(layer_2[0][0])# store hidden layer so we can use it in the next timesteplayer_1_values.append(copy.deepcopy(layer_1))future_layer_1_delta = np.zeros(hidden_dim)for position in range(binary_dim):X = np.array([[a[position],b[position]]])layer_1 = layer_1_values[-position-1]prev_layer_1 = layer_1_values[-position-2]# error at output layerlayer_2_delta = layer_2_deltas[-position-1]# error at hidden layerlayer_1_delta = (future_layer_1_delta.dot(synapse_h.T) + \layer_2_delta.dot(synapse_1.T)) * sigmoid_output_to_derivative(layer_1)# let's update all our weights so we can try againsynapse_1_update += np.atleast_2d(layer_1).T.dot(layer_2_delta)synapse_h_update += np.atleast_2d(prev_layer_1).T.dot(layer_1_delta)synapse_0_update += X.T.dot(layer_1_delta)future_layer_1_delta = layer_1_deltasynapse_0 += synapse_0_update * alphasynapse_1 += synapse_1_update * alphasynapse_h += synapse_h_update * alpha    synapse_0_update *= 0synapse_1_update *= 0synapse_h_update *= 0# print out progressif(j % 1000 == 0):print "Error:" + str(overallError)print "Pred:" + str(d)print "True:" + str(c)out = 0for index,x in enumerate(reversed(d)):out += x*pow(2,index)print str(a_int) + " + " + str(b_int) + " = " + str(out)print "------------"

运行输出：

Error:[ 3.45638663]
Pred:[0 0 0 0 0 0 0 1]
True:[0 1 0 0 0 1 0 1]
9 + 60 = 1
------------
Error:[ 3.63389116]
Pred:[1 1 1 1 1 1 1 1]
True:[0 0 1 1 1 1 1 1]
28 + 35 = 255
------------
Error:[ 3.91366595]
Pred:[0 1 0 0 1 0 0 0]
True:[1 0 1 0 0 0 0 0]
116 + 44 = 72
------------
Error:[ 3.72191702]
Pred:[1 1 0 1 1 1 1 1]
True:[0 1 0 0 1 1 0 1]
4 + 73 = 223
------------
Error:[ 3.5852713]
Pred:[0 0 0 0 1 0 0 0]
True:[0 1 0 1 0 0 1 0]
71 + 11 = 8
------------
Error:[ 2.53352328]
Pred:[1 0 1 0 0 0 1 0]
True:[1 1 0 0 0 0 1 0]
81 + 113 = 162
------------
Error:[ 0.57691441]
Pred:[0 1 0 1 0 0 0 1]
True:[0 1 0 1 0 0 0 1]
81 + 0 = 81
------------
Error:[ 1.42589952]
Pred:[1 0 0 0 0 0 0 1]
True:[1 0 0 0 0 0 0 1]
4 + 125 = 129
------------
Error:[ 0.47477457]
Pred:[0 0 1 1 1 0 0 0]
True:[0 0 1 1 1 0 0 0]
39 + 17 = 56
------------
Error:[ 0.21595037]
Pred:[0 0 0 0 1 1 1 0]
True:[0 0 0 0 1 1 1 0]
11 + 3 = 14
------------

第一部分：什么是神经元记忆？

正向的背一边字母表……你能做到，对吧？

倒着背一遍字母表……唔……也许有点难。

那么试试你熟悉的一首歌词？……为什么正常顺序回忆的时候比倒着回忆更简单呢？你能直接跳跃到第二小节的歌词么？……唔唔……同样很难，是吧？

其实这很符合逻辑……你并不像计算机那样把字母表或者歌词像存储在硬盘一样的记住，你是把它们作为一个序列去记忆的。你很擅长于一个单词一个单词的去回忆起它们，这是一种条件记忆。你只有在拥有了前边部分的记忆了以后，才能想起来后边的部分。如果你对链表比较熟悉的话，OK，我们的记忆就和链表是类似的。

然而，这并不意味着当你不唱歌时，你的记忆中就没有这首歌。而是说，当你试图直接记忆起某个中间的部分，你需要花费一定的时间在你的脑海中寻找（也许是在一大堆神经元里寻找）。大脑开始在这首歌里到处寻找你想要的中间部分，但是大脑之前并没有这么做过，所以它并没有一个能够指向中间这部分的索引。这就像住在一个附近都是岔路/死胡同的地方，你从大路上到某人的房子很简单，因为你经常那样走。但是把你丢在一家人的后院里，你却怎么也找不到正确的道路了。可见你的大脑并不是用“方位”去寻找，而是通过一首歌的开头所在的神经元去寻找的。如果你想了解更多关于大脑的知识，可以访问：http://www.human-memory.net/processes_recall.html。

就像链表一样，记忆这样去存储是很有效的。这样可以通过脑神经网络很好的找到相似的属性、优势。一些过程、难题、表示、查询也可以通过这种短期/伪条件记忆序列存储的方式，使其更加的高效。

去记忆一些数据是序列的事情（其实就是意味着你有些东西需要去记住！），假设有一个跳跳球，每个数据点就是你眼中跳跳球运动的一帧图像。如果你想训练一个神经网络去预测下一帧球会在哪里，那么知道上一帧球在哪里就会对你的预测很有帮助！这样的序列数据就是我们为什么要搭建一个循环神经网络。那么，一个神经网络怎么记住它之前的时间它看到了什么呢？

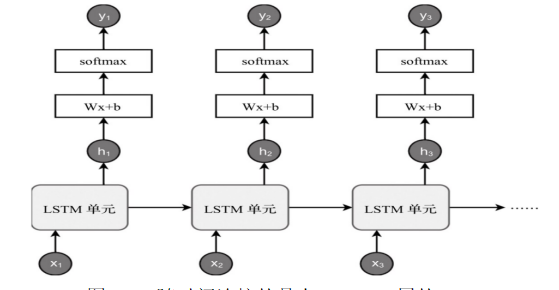
神经网络有隐藏层，一般来讲，隐藏层的状态只跟输入数据有关。所以一般来说一个神经网络的信息流就会像下面所示的这样：

input -> hidden ->output

这很明显，确定的输入产生确定的隐藏层，确定的隐藏层产生确定的输出层。这是一种封闭系统。但是，记忆改变了这种模式！记忆意味着隐藏层是，当前时刻的输入与隐藏层前一时刻的一种组合。

( input + prev_hidden ) -> hidden -> output

为什么是隐藏层呢？其实技术上来说我们可以这样：

( input + prev_input ) -> hidden -> output

然而，我们遗漏了一些东西。我建议你认真想想这两个信息流的不同。给你点提示，演绎一下它们分别是怎么运作的。这里呢，我们给出4步的循环神经网络流程看看它怎么从之前的隐藏层得到信息。

( input + empty_hidden ) -> hidden -> output

( input + prev_hidden ) -> hidden -> output

然后，我们再给出4步，从输入层怎么得到信息。

( input + empty_input ) -> hidden -> output

( input + prev_input ) -> hidden -> output

或许，如果我把一些部分涂上颜色，一些东西就显而易见了。那么我们再看看这4步隐藏层的循环：

( input + empty_hidden ) ->hidden -> output

( input + prev_hidden ) ->hidden -> output

……以及，4步输入层的循环：

( input + empty_input ) -> hidden -> output

( input + prev_input ) -> hidden -> output

看一下最后一个隐藏层（第四行）。在隐藏层循环中，我们可以看到所有见过的输入的存在。但是在输入层循环中，我们仅仅能发现上次与本次的输入。这就是为什么我们用隐藏层循环建模。隐藏层循环能学习它到底去记忆什么，但是输入层循环仅仅能记住上次的数据点。

现在我们对比一下这两种方法，通过反向的字母表与歌词中间部分的练习。隐藏层根据越来越多的输入持续的改变，而且，我们到达这些隐藏状态的唯一方式就是沿着正确的输入序列。现在就到了很重要的一点，输出由隐藏层决定，而且只有通过正确的输入序列才能到达隐藏层。是不是很相似？

那么有什么实质的区别呢？我们考虑一下我们要预测歌词中的下一个词，假如碰巧在不同的地方有两个相同的词，“输出层循环”就会使你回忆不起来下面的歌词到底是什么了。仔细想想，如果一首歌有一句“我爱你”，以及“我爱萝卜”，记忆网络现在试图去预测下一个词，那它怎么知道“我爱”后边到底是什么？可能是“你”，也可能是“萝卜”。所以记忆网络必须要知道更多的信息，去识别这到底是歌词中的那一段。而“隐藏层循环”不会让你忘记歌词，就是通过这个原理。它巧妙地记住了它看到的所有东西（记忆更巧妙地是它能随时间逐渐忘却）。想看看它是怎么运作的，猛戳这里：http://karpathy.github.io/2015/05/21/rnn-effectiveness/

好的，现在停下来，然后确认你的脑袋是清醒的。

第二部分：RNN - 神经网路记忆

现在我们已经对这个问题有个直观的认识了，让我们下潜的更深一点（什么鬼，你在逗我？）。就像在反向传播这篇博文（http://blog.csdn.net/zzukun/article/details/49556715）里介绍的那样，输入数据决定了我们神经网络的输入层。每行输入数据都被用来产生隐含层（通过正向传播），然后用每个隐含层生成输出层（假设只有一层隐含层）。就像我们刚才看到的，记忆意味着隐含层是输入与上一次隐含层的组合。那么怎么组合呢？其实就像神经网络的其他传播方法，用一个矩阵就行了，这个矩阵定义了之前隐含层与当前的关系。

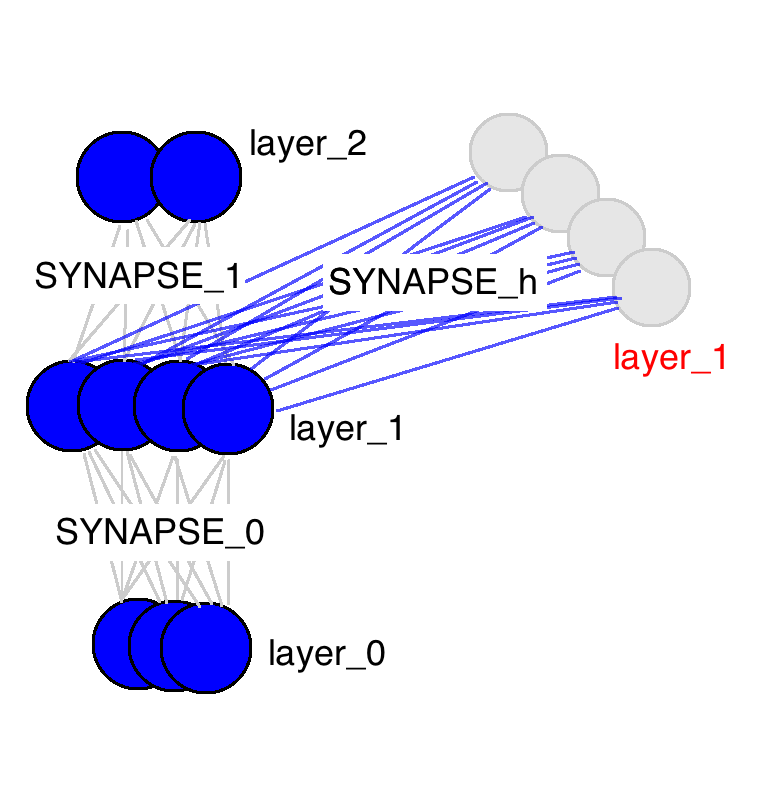
从这张图中能看出来很多东西。这里只有三个权值矩阵，其中两个很相似（名字也一样）。SYNAPSE_0把输入数据传播到隐含层，SYNAPSE_1把隐含层数据传播到输出层。新的矩阵（SYNAPSE_h……要循环的），把隐含层（layer_1）传播到下一个时间点的隐含层（仍旧是layer_1）。

好的，现在停下来，然后确认你的脑袋是清醒的。

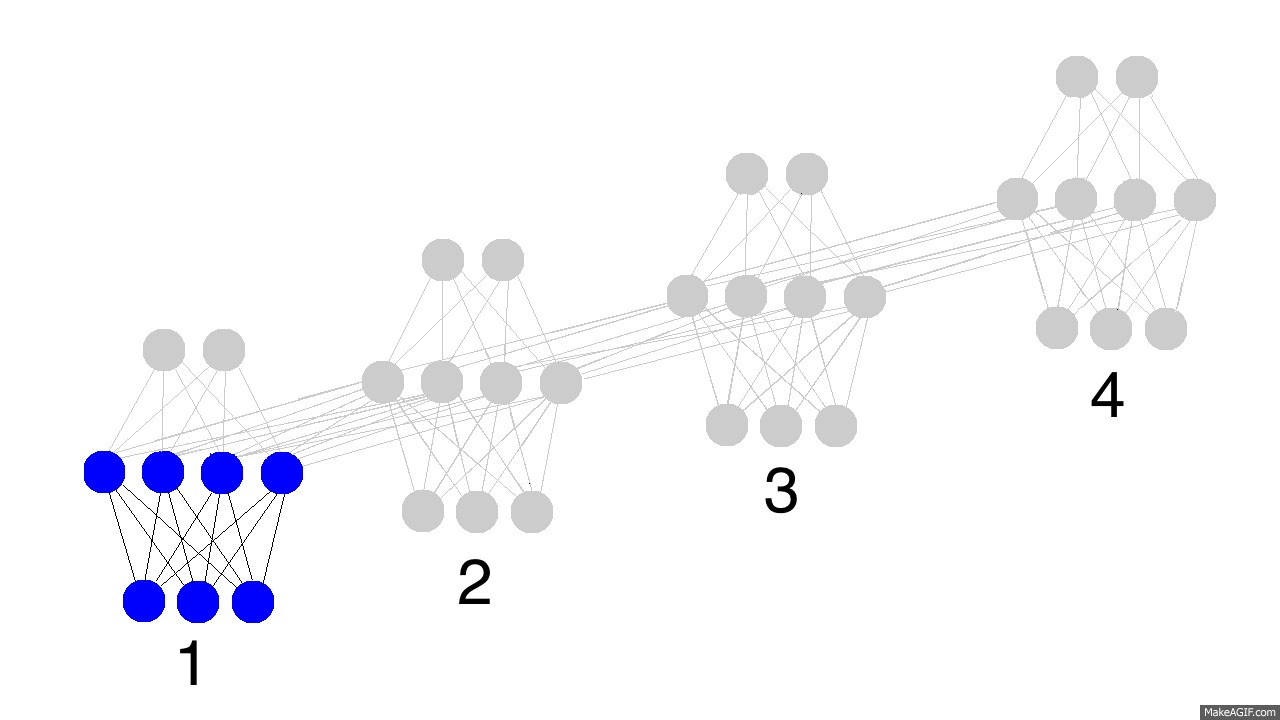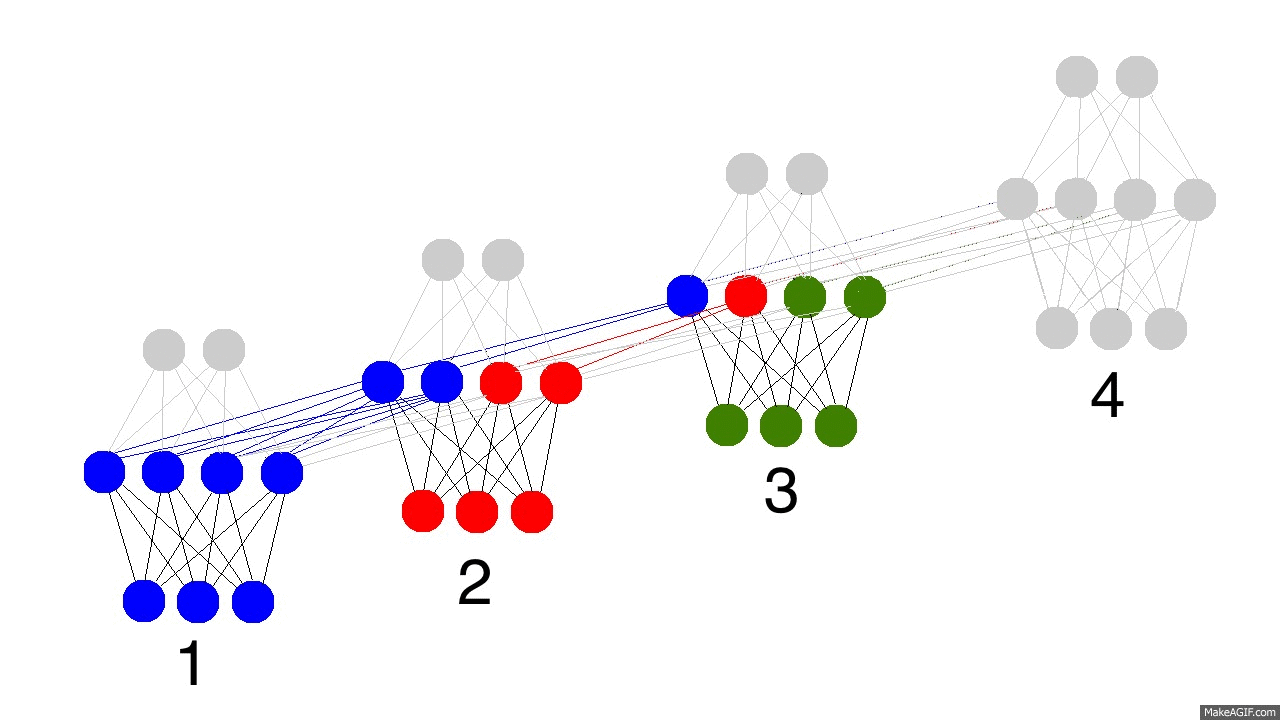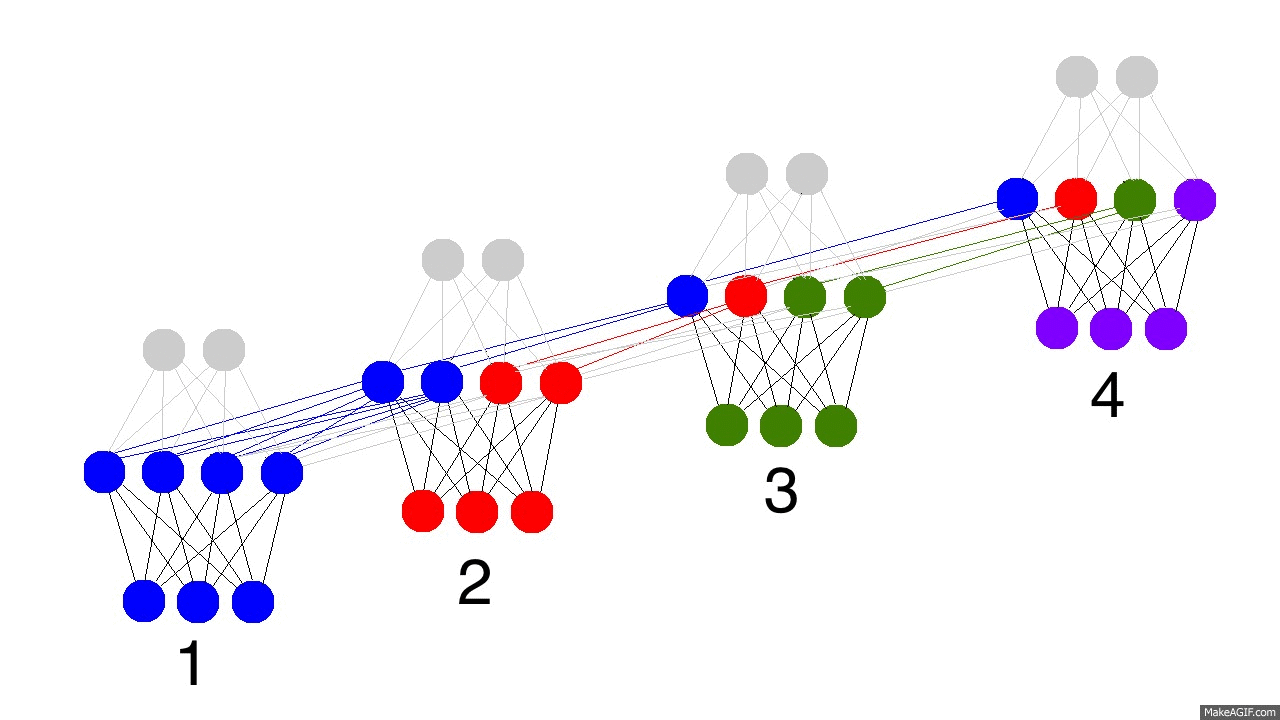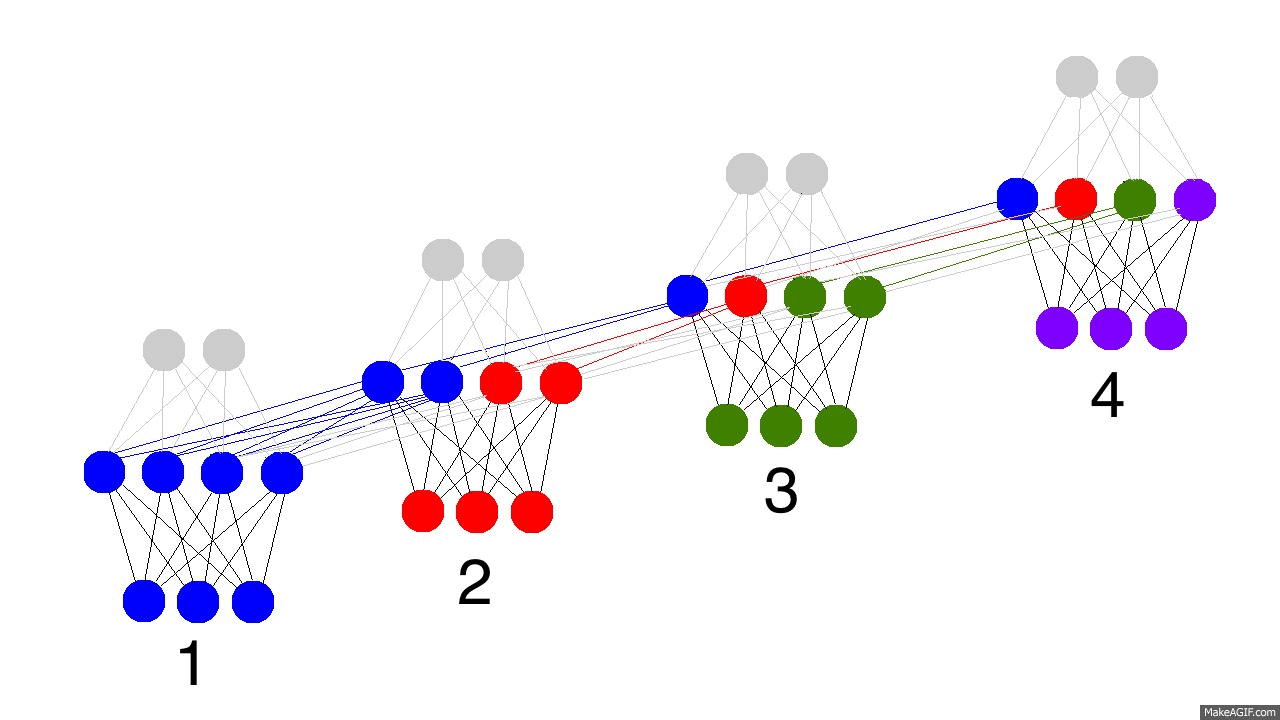
上边的GIF图展现出循环神经网络的奥秘，以及一些非常、非常重要的性质。图中描述了4个时间步数，第一个仅仅受到输入数据的影响，第二个把第二个输入与第一个的隐含层混合，如此继续。有人可能会注意到，在这种方式下，第四个网络“满了”。这样推测的话，第五步不得不选择一个某个节点去替代掉它。是的，这很正确。这就是记忆的“容量”概念。正如你所期望的，更多的隐含层节点能够存储更多的记忆，并使记忆保持更长的时间。同样这也是网络学习去忘记无关的记忆并且记住重要的记忆。你在能从第三步中看出点什么不？为什么有更多的绿色节点呢？

另外需要注意的是，隐含层是输入与输出中间的一道栅栏。事实上，输出已经不再是对应于输入的一个函数。输入只是改变了记忆中存储的东西，而且输出仅仅依赖于记忆！告诉你另外一个有趣的事情，如果上图中的第2,3,4步没有输入，随着时间的流逝，隐含层仍然会改变。

好的，好的，我知道你已经停下来了，不过一定要保证刚才的内容你已经差不多理解了。

第三部分：基于时间的反向传播

那么现在问题来了，循环神经网络怎么学习的呢？看下面的图片，黑色的是预测，误差是亮黄色，导数是芥末色的（暗黄色）。

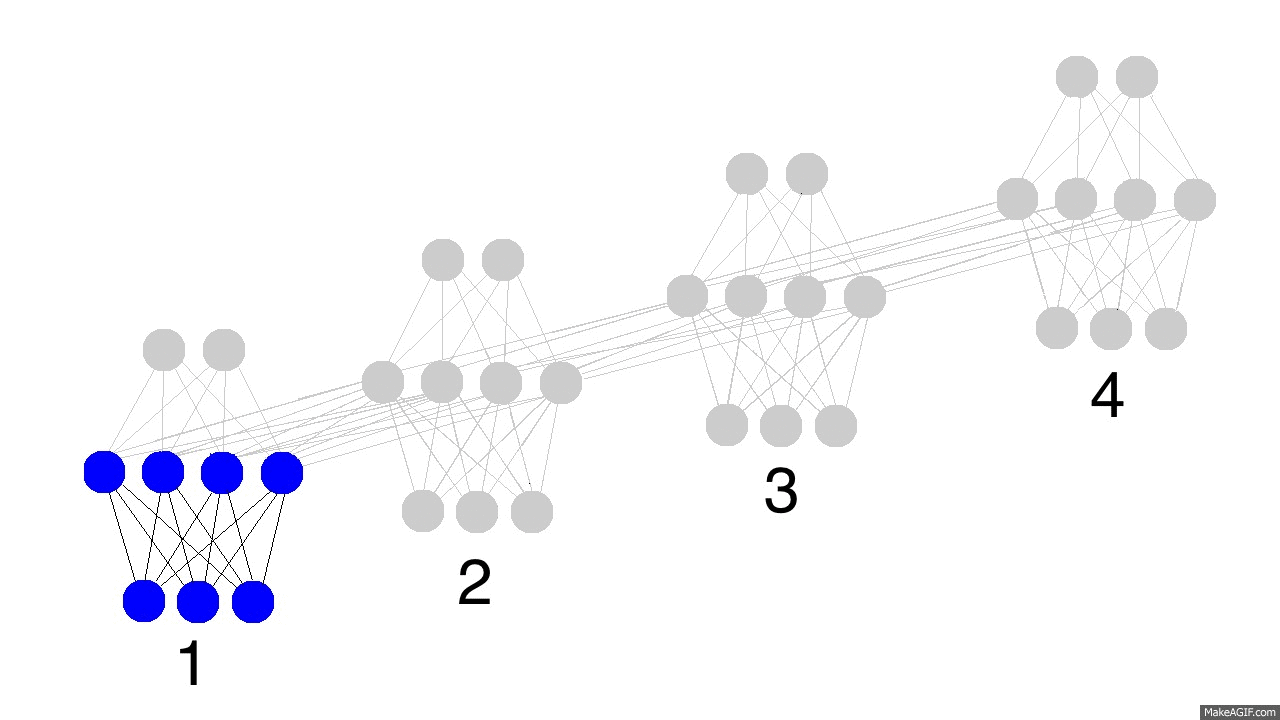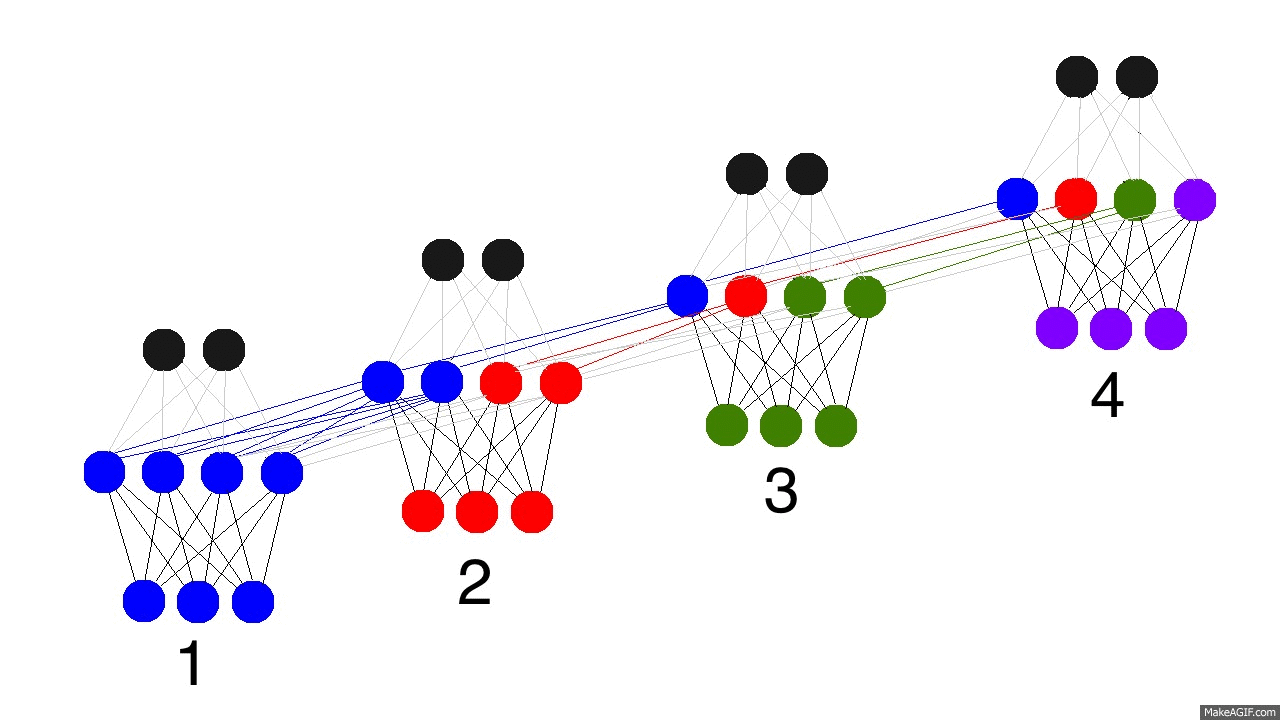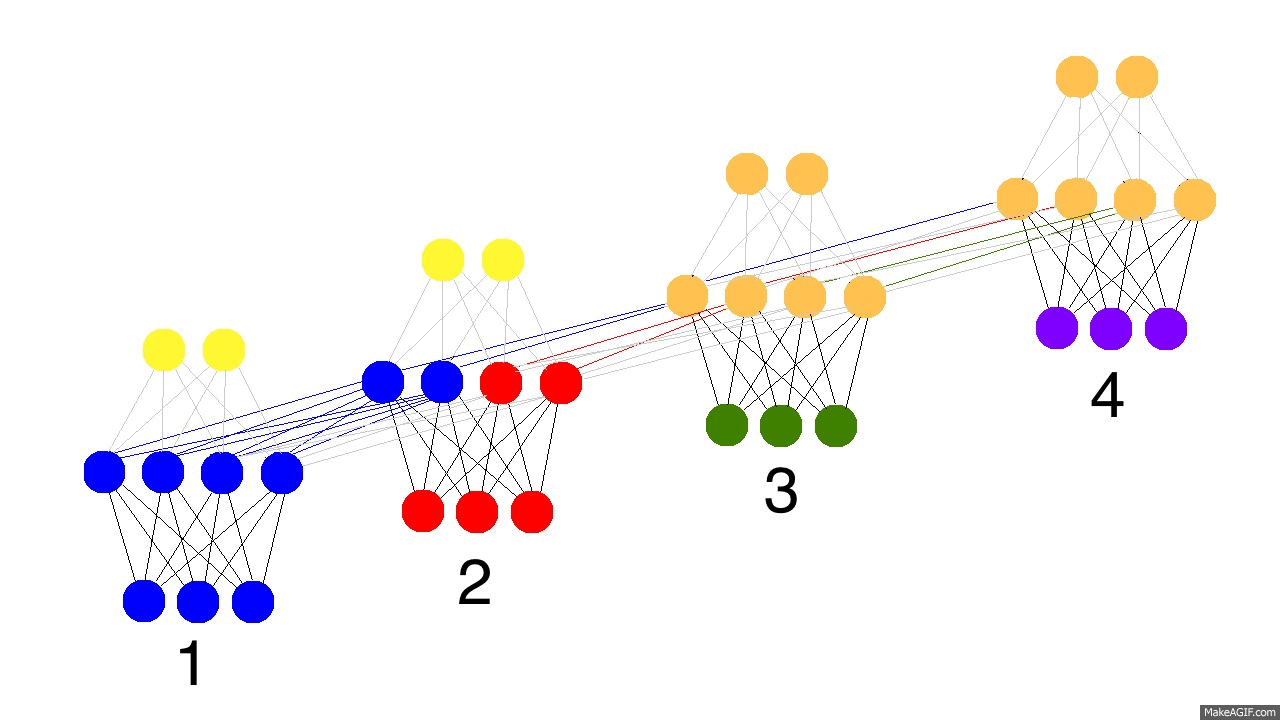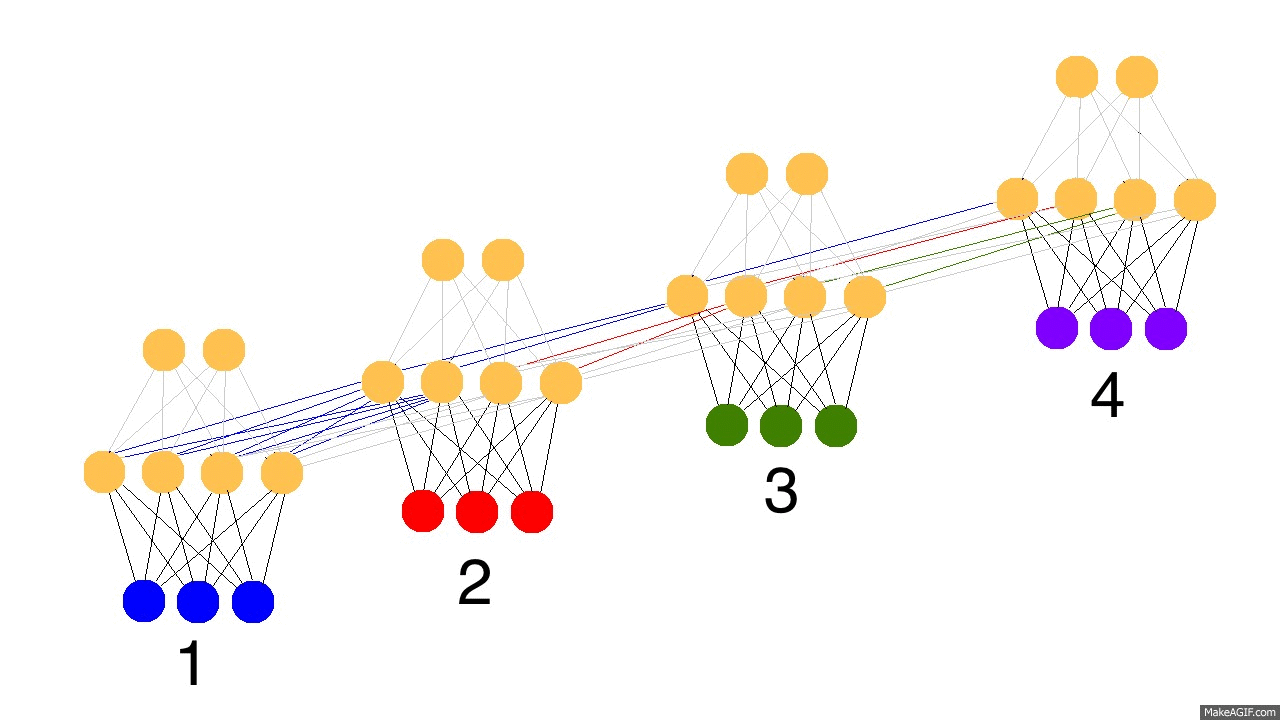
网络通过从1到4的全部传播（通过任意长度的整个序列），然后从4到1反向传播所有的导数值。你也可以认为这仅仅是正常神经网络的一个有意思的变形，除了我们在各自的地方复用了相同的权值（突触synapses 0,1,h）。其他的地方都是很普通的反向传播。

第四部分：我们的玩具代码

我们现在使用循环神经网络去建模二进制加法。你看到下面的序列了么？上边这俩在方框里的，有颜色的1是什么意思呢？

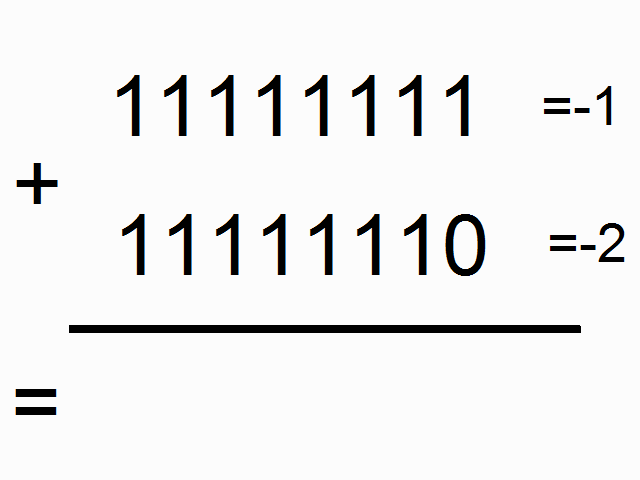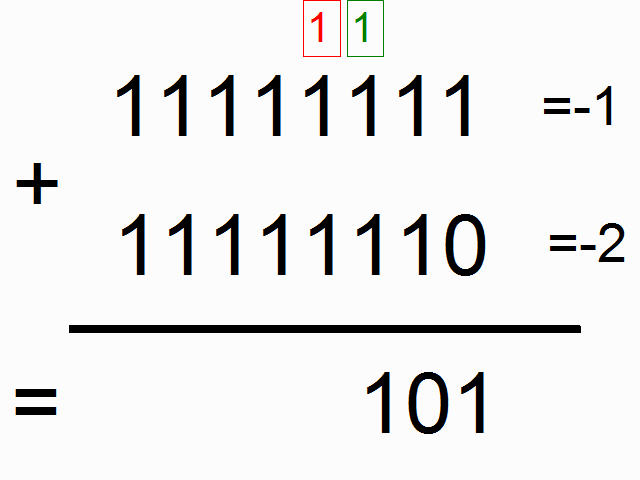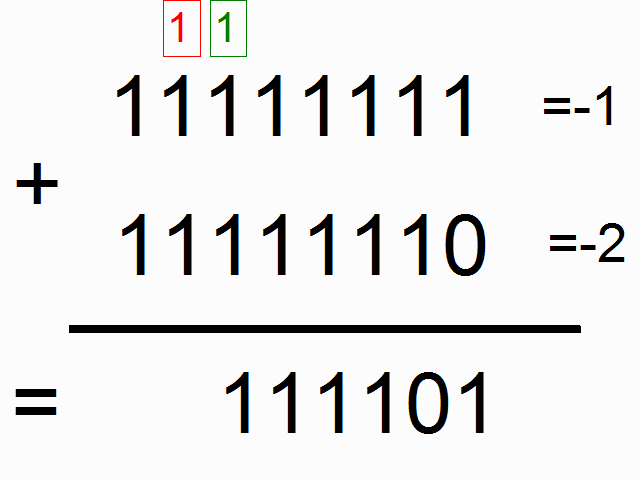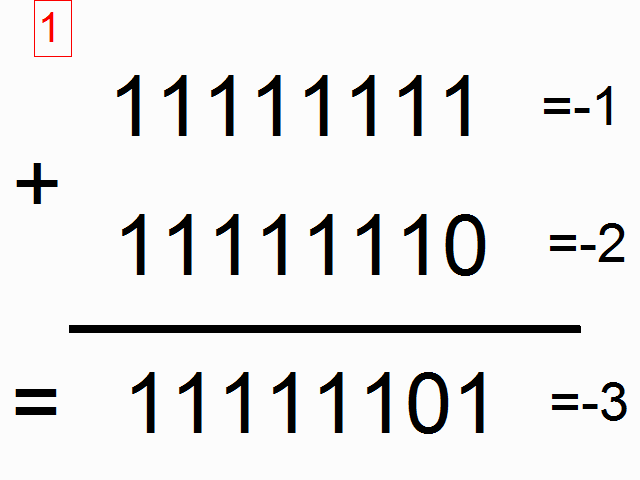
框框中彩色的1表示“携带位”。当每个位置的和溢出时（需要进位），它们“携带这个‘1’”。我们就是要教神经网络学习去记住这个“携带位”。当“和”需要它，它需要去“携带这个‘1’”。

二进制加法从右边到左边进行计算，我们试图通过上边的数字，去预测横线下边的数字。我们想让神经网络遍历这个二进制序列并且记住它携带这个1与没有携带这个1的时候，这样的话网络就能进行正确的预测了。不要迷恋于这个问题本身，因为神经网络事实上也不在乎。就当作我们有两个在每个时间步数上的输入（1或者0加到每个数字的开头），这两个输入将会传播到隐含层，隐含层会记住是否有携带位。预测值会考虑所有的信息，然后去预测每个位置（时间步数）正确的值。

下面我推荐同时打开两个这个页面，这样就可以一边看代码，一边看下面的解释。我就是这么写这篇文章的。

Lines 0-2:导入依赖包，设定随机数生成的种子。我们只需要两个依赖包，numpy和copy。numpy是为了矩阵计算，copy用来拷贝东西。

Lines 4-11:我们的非线性函数与其导数，更多的细节可见参考我们之前的博客：http://blog.csdn.net/zzukun/article/details/49556715

Line 15:这一行声明了一个查找表，这个表是一个实数与对应二进制表示的映射。二进制表示将会是我们网路的输入与输出，所以这个查找表将会帮助我们将实数转化为其二进制表示。

Line 16:这里设置了二进制数的最大长度。如果一切都调试好了，你可以把它调整为一个非常大的数。

Line 18:这里计算了跟二进制最大长度对应的可以表示的最大十进制数。

Line 19:这里生成了十进制数转二进制数的查找表，并将其复制到int2binary里面。虽然说这一步不是必需的，但是这样的话理解起来会更方便。

Line 26:这里设置了学习速率。

Line 27:我们要把两个数加起来，所以我们一次要输入两位字符。如此以来，我们的网络就需要两个输入。

Line 28:这是隐含层的大小，回来存储“携带位”。需要注意的是，它的大小比原理上所需的要大。自己尝试着调整一下这个值，然后看看它如何影响收敛速率。更高的隐含层维度会使训练变慢还是变快？更多或是更少的迭代次数？

Line 29:我们只是预测和的值，也就是一个数。如此，我们只需一个输出。

Line 33:这个权值矩阵连接了输入层与隐含层，如此它就有“imput_dim”行以及“hidden_dim”列（假如你不改参数的话就是2×16）。

Line 34:这个权值矩阵连接了隐含层与输出层，如此它就有“hidden_dim”行以及“output_dim”列（假如你不改参数的话就是16×1）。

Line 35:这个权值矩阵连接了前一时刻的隐含层与现在时刻的隐含层。它同样连接了当前时刻的隐含层与下一时刻的隐含层。如此以来，它就有隐含层维度大小（hidden_dim）的行与隐含层维度大小（hidden_dim）的列（假如你没有修改参数就是16×16）。

Line 37-39:这里存储权值更新。在我们积累了一些权值更新以后，我们再去更新权值。这里先放一放，稍后我们再详细讨论。

Line 42:我们迭代训练样例10000次。

Line 45:这里我们要随机生成一个在范围内的加法问题。所以我们生成一个在0到最大值一半之间的整数。如果我们允许网络的表示超过这个范围，那么把两个数加起来就有可能溢出（比如一个很大的数导致我们的位数不能表示）。所以说，我们只把加法要加的两个数字设定在小于最大值的一半。

Line 46:我们查找a_int对应的二进制表示，然后把它存进a里面。

Line 48:原理同45行。

Line 49:原理同46行。

Line 52:我们计算加法的正确结果。

Line 53:把正确结果转化为二进制表示。

Line 56:初始化一个空的二进制数组，用来存储神经网络的预测值（便于我们最后输出）。你也可以不这样做，但是我觉得这样使事情变得更符合直觉。

Line 58:重置误差值（这是我们使用的一种记录收敛的方式……可以参考之前关于反向传播与梯度下降的文章）

Line 60-61:这两个list会每个时刻不断的记录layer 2的导数值与layer 1的值。

Line 62:在0时刻是没有之前的隐含层的，所以我们初始化一个全为0的。

Line 65:这个循环是遍历二进制数字。

Line 68:X跟图片中的“layer_0”是一样的，X数组中的每个元素包含两个二进制数，其中一个来自a，一个来自b。它通过position变量从a，b中检索，从最右边往左检索。所以说，当position等于0时，就检索a最右边的一位和b最右边的一位。当position等于1时，就向左移一位。

Line 69:跟68行检索的方式一样，但是把值替代成了正确的结果（0或者1）。

Line 72:这里就是奥妙所在！一定一定一定要保证你理解这一行！！！为了建立隐含层，我们首先做了两件事。第一，我们从输入层传播到隐含层（np.dot(X,synapse_0)）。然后，我们从之前的隐含层传播到现在的隐含层（np.dot(prev_layer_1.synapse_h)）。在这里，layer_1_values[-1]就是取了最后一个存进去的隐含层，也就是之前的那个隐含层！然后我们把两个向量加起来！！！！然后再通过sigmoid函数。

那么，我们怎么结合之前的隐含层信息与现在的输入呢？当每个都被变量矩阵传播过以后，我们把信息加起来。

Line 75:这行看起来很眼熟吧？这跟之前的文章类似，它从隐含层传播到输出层，即输出一个预测值。

Line 78:计算一下预测误差（预测值与真实值的差）。

Line 79:这里我们把导数值存起来（上图中的芥末黄），即把每个时刻的导数值都保留着。

Line 80:计算误差的绝对值，并把它们加起来，这样我们就得到一个误差的标量（用来衡量传播）。我们最后会得到所有二进制位的误差的总和。

Line 86:将layer_1的值拷贝到另外一个数组里，这样我们就可以下一个时间使用这个值。

Line 90:我们已经完成了所有的正向传播，并且已经计算了输出层的导数，并将其存入在一个列表里了。现在我们需要做的就是反向传播，从最后一个时间点开始，反向一直到第一个。

Line 92:像之前那样，检索输入数据。

Line 93:从列表中取出当前的隐含层。

Line 94:从列表中取出前一个隐含层。

Line 97:从列表中取出当前输出层的误差。

Line 99:这一行计算了当前隐含层的误差。通过当前之后一个时间点的误差和当前输出层的误差计算。

Line 102-104:我们已经有了反向传播中当前时刻的导数值，那么就可以生成权值更新的量了（但是还没真正的更新权值）。我们会在完成所有的反向传播以后再去真正的更新我们的权值矩阵，这是为什么呢？因为我们要用权值矩阵去做反向传播。如此以来，在完成所有反向传播以前，我们不能改变权值矩阵中的值。

Line 109-115:现在我们就已经完成了反向传播，得到了权值要更新的量，所以就赶快更新权值吧（别忘了重置update变量）！

Line 118-end:这里仅仅是一些输出日志，便于我们观察中间的计算过程与效果。