LSTM神经网络图详解
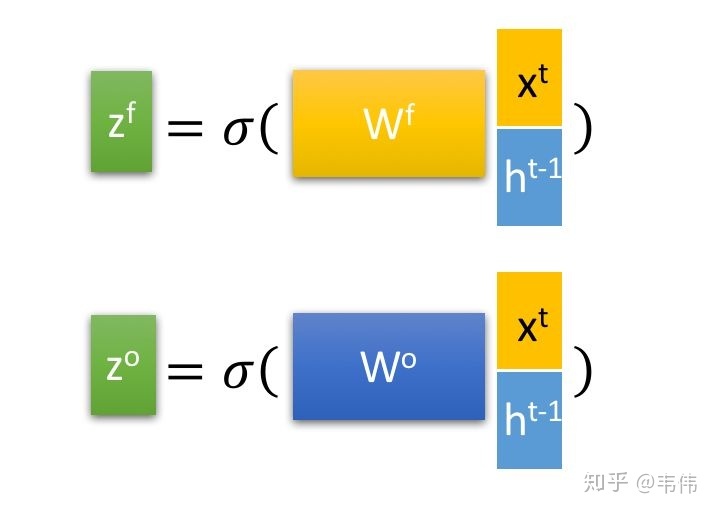
(1)遗忘门,用于计算信息的遗忘(保留)程度,通过sigmoid处理后为0到1的值,1表示全部保留,0表示全部忘记。 f t = σ ( W f ⋅ [ h t − 1 , x t ] + b f ) f_{t}=\sigma \left ( W_{f}\cdot \left [ h_{t-1},x_{t} \right ] +b_{f}\right ) ft=σ(Wf⋅[ht−1,xt]+bf)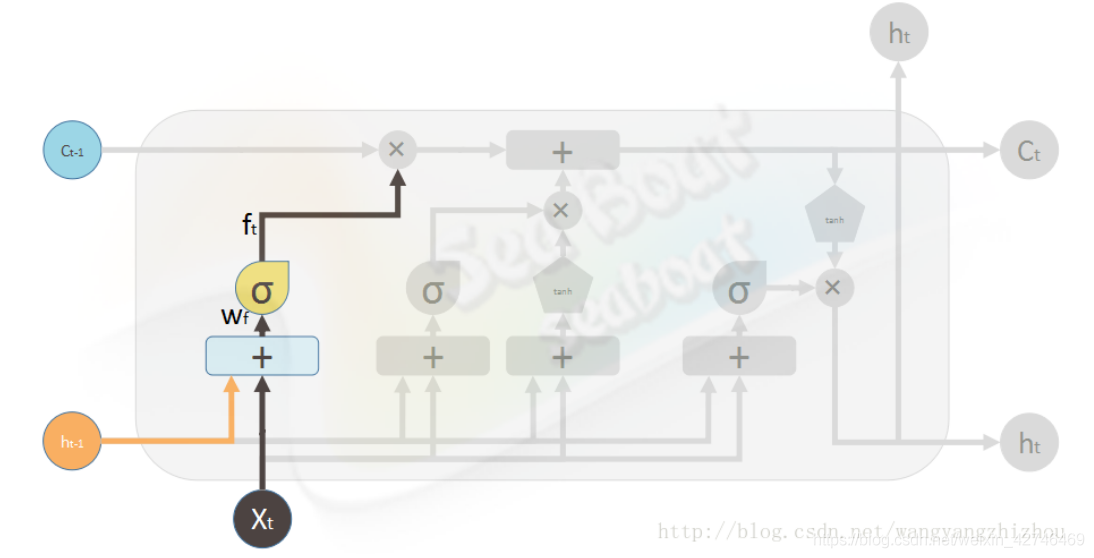
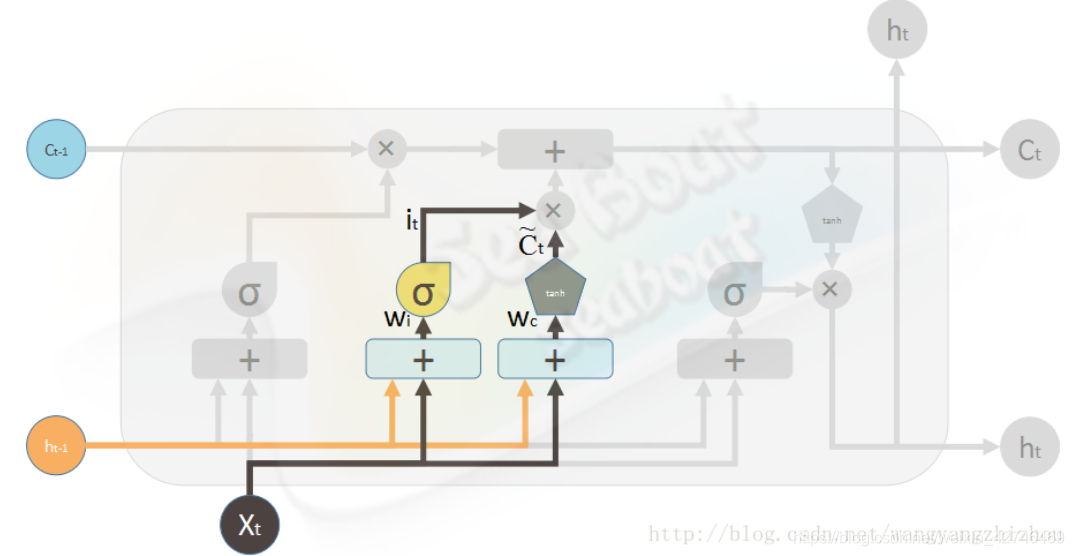
(2)输入门,输入门用来计算哪些信息保存到状态单元中,包括两部分信息,一部分是
i t = σ ( W i ⋅ [ h t − 1 , x t ] + b i ) i_{t}=\sigma \left ( W_{i}\cdot \left [ h_{t-1},x_{t} \right ] +b_{i}\right ) it=σ(Wi⋅[ht−1,xt]+bi)
该部分可以看成当前输入有多少信息需要保存到单元状态。另一部分是
c t ~ = tanh ( W c ⋅ [ h t − 1 , x t ] + b c ) \tilde{c_{t}}=\tanh \left ( W_{c}\cdot \left [ h_{t-1},x_{t} \right ] +b_{c}\right ) ct~=tanh(Wc⋅[ht−1,xt]+bc)
该部分用来把当前输入产生的新信息添加到单元状态中。这两部分产生新的记忆状态。
由此,当前时刻的单元状态由遗忘门输入和上一时刻状态的积加上输入门两部分的积,即
c t = f t ⋅ c t − 1 + i t ⋅ c ~ t {c_{t}}= f_{t}\cdot c_{t-1}+ i_{t}\cdot \tilde c_{t} ct=ft⋅ct−1+it⋅c~t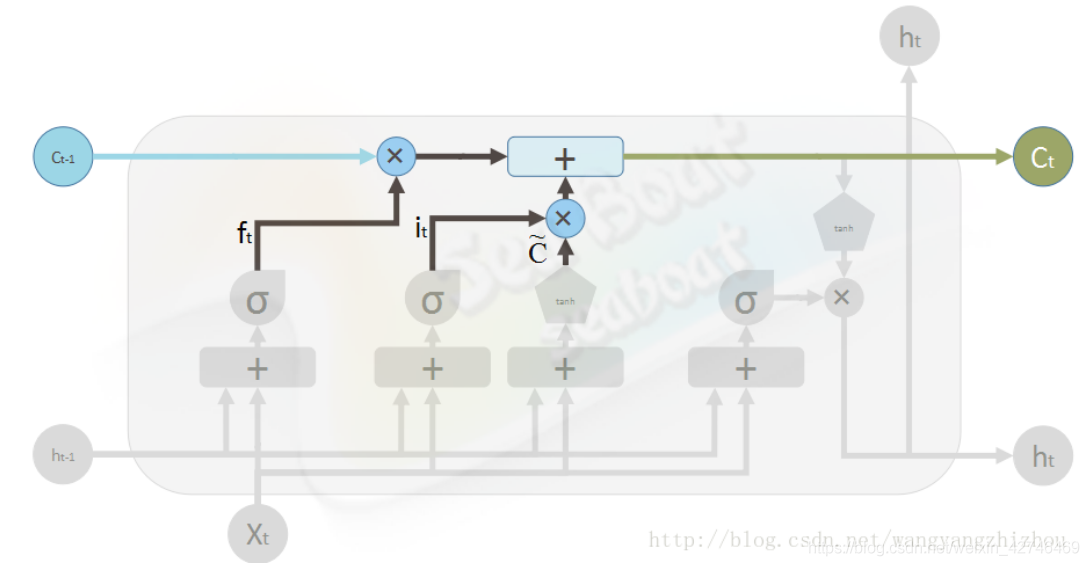
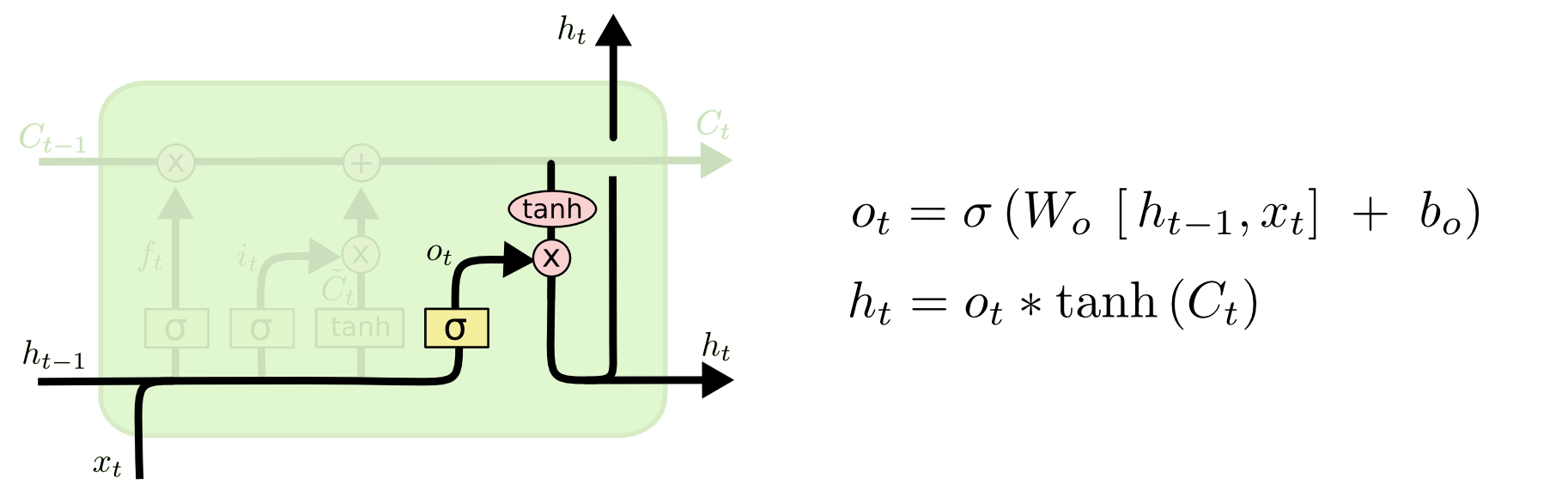
(3)输出门,用于计算当前时刻信息被输出的程度。
o t = σ ( W o ⋅ [ h t − 1 , x t ] + b o ) o_{t}=\sigma \left ( W_{o}\cdot \left [ h_{t-1},x_{t} \right ] +b_{o}\right ) ot=σ(Wo⋅[ht−1,xt]+bo)
h t = o t ⋅ t a n h ( c t ) h_{t}= o_{t}\cdot tanh(c_{t}) ht=ot⋅tanh(ct)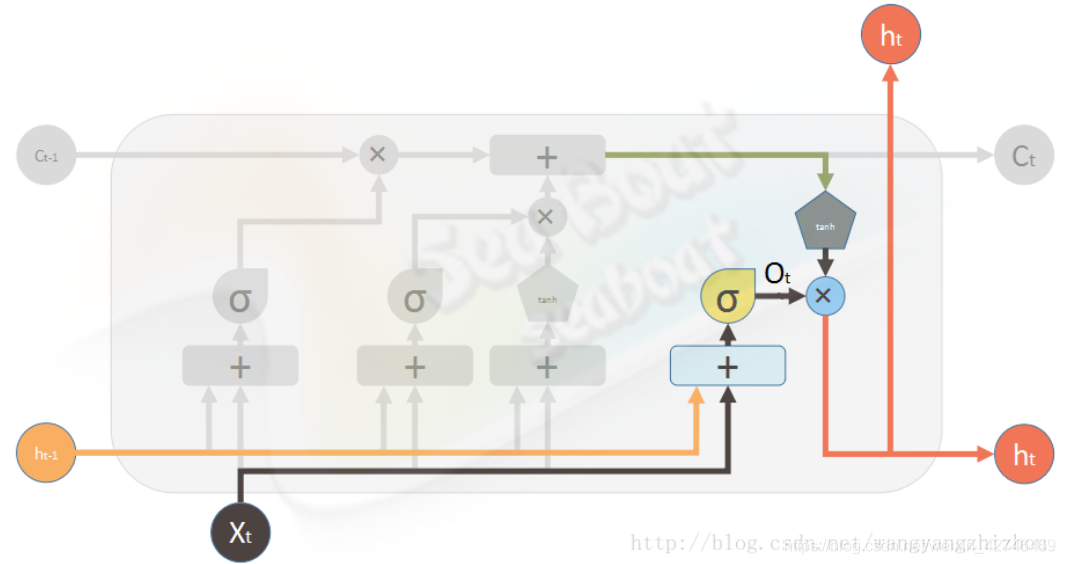
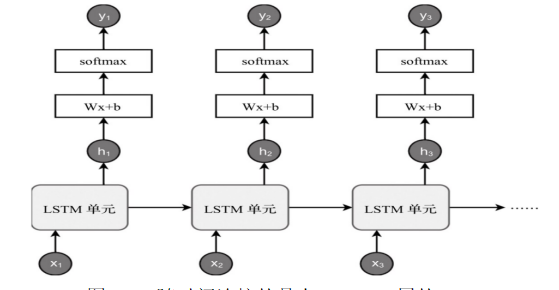
整个LSTM神经网络就是如此,下面是李宏毅老师ppt上的,可以进一步了解整个流程。PPT链接循环神经网络
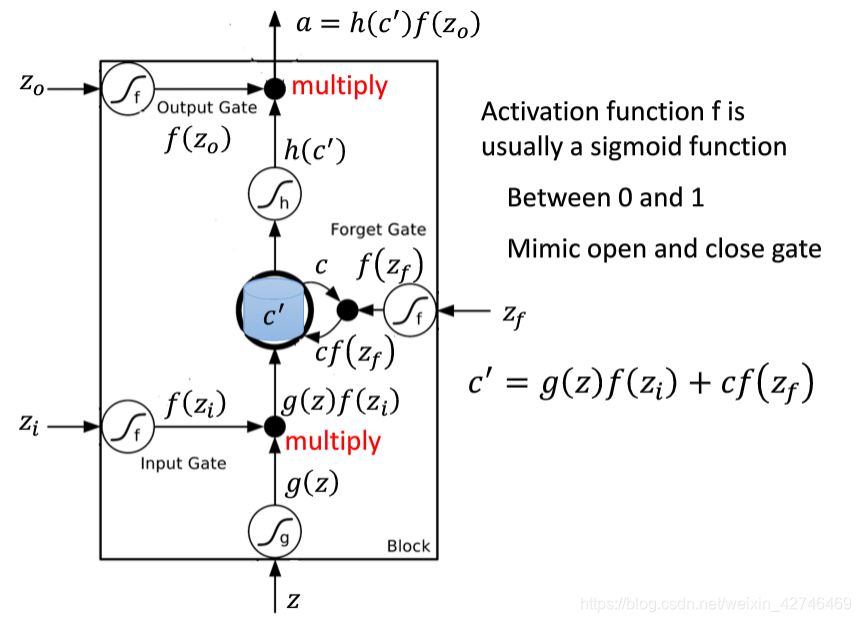
对于门(Gate)的理解,这里有很形象的解释深度学习计算模型中“门函数(Gating Function)”的作用
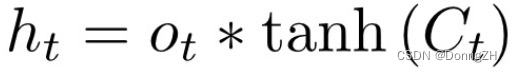
![[深入浅出] LSTM神经网络](https://img-blog.csdnimg.cn/img_convert/d9fa736dddf779de72df0c72172cf225.png)