魔方阵 概念
魔方阵,古代又称“纵横图”,是指组成元素为自然数1、2…n的平方的n×n的方阵,其中每个元素值都不相等,且每行、每列以及主、副对角线上各n个元素之和都相等。阶数大于等于3。
如3×3的魔方阵:
8 1 6
3 5 7
4 9 2
奇数魔方阵
奇数魔方阵的排列规律如下:
(1)将1放在第一行中间一列;
(2)从2开始直到n×n止各数依次按下列规则存放;每一个数存放的行比前一个数的行数减1,列数加1(例如上面的三阶魔方阵,5在4的上一行后一列);
(3)如果上一个数的行数为1,则下一个数的行数为n(指最下一行);例如1在第一行,则2应放在最下一行,列数同样加1;
(4)当上一个数的列数为n时,下一个数的列数应为1,行数减去1。例如2在第3行最后一列,则3应放在第二行第一列;
(5)如果按上面规则确定的位置上已有数,或上一个数是第一行第n列时,则把下一个数放在上一个数的下面。例如按上面的规定,4应该放在第1行第2列,但该位置已经被占据,所以4就放在3的下面;
代码:以5*5魔方阵为例
#include <iostream>
using namespace std;
int main()
{int n=5;int a[n][n];//初始化n*n数组for(int i=0;i<n;i++)for(int j=0;j<n;j++)a[i][j]=-1;//1放在第一行中间列int r=0;int c=n/2; // row, columna[r][c]=1;for(int i=2;i<=n*n;i++){//目标行if(r==0) r=n-1;else r=r-1;//目标列c=(c+1)%n;//如果目标位置未被占用,赋值,否则放到上一个数的下方if(a[r][c]==-1){ a[r][c]=i;}else{//上一个数的r,c r=(r+1)%n;if(c==0) c=n-1;else c=c-1;//待放数的位置r=(r+1)%n;//c=c; a[r][c]=i; }}for(int i=0;i<n;i++){for(int j=0;j<n;j++)cout<<a[i][j]<<'\t';cout<<endl; }return 0;
}
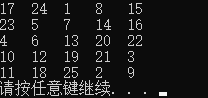
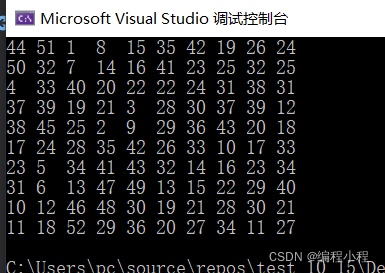
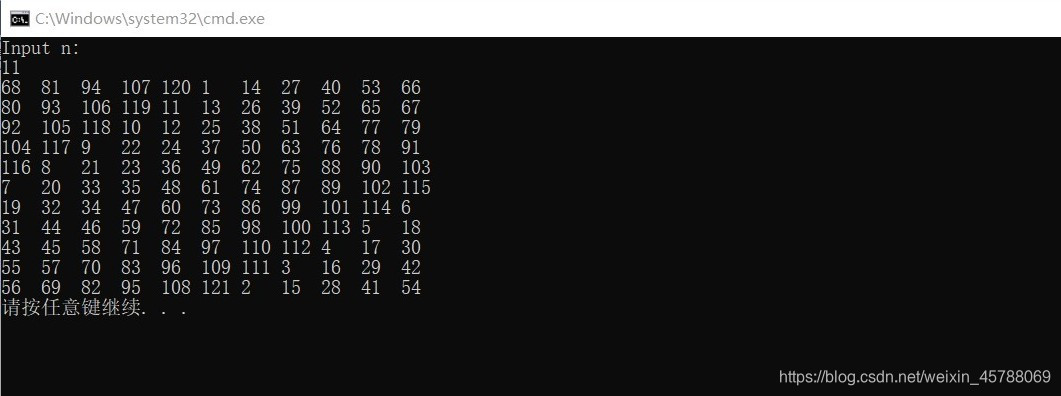
运行结果