L1 loss & L2 loss & Smooth L1 loss

微信公众号：幼儿园的学霸
个人的学习笔记，关于OpenCV,关于机器学习, …。问题或建议，请公众号留言;

关于神经网络中L1 loss & L2 loss & Smooth L1 loss损失函数的对比、优缺点分析

目录

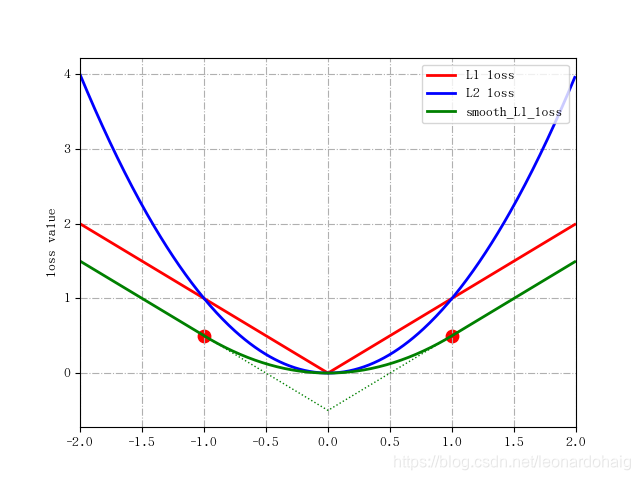
损失函数曲线如图所示：

L1 Loss

也就是L1 Loss了，它有几个别称：

• L1 范数损失
• 最小绝对值偏差（LAD，LeastAbsolute Deviation）
• 最小绝对值误差（LAE，LeastAbsolute error）
  最常看到的MAE也是指L1 Loss损失函数。 它是把期望值Y 与模型输出值（预测值）f(x)的差 做绝对值得到的误差（添加了绝对值之后意味着该误差只用考虑误差幅度，不用考虑误差的方向，如果未加绝对值，意味着误差是考虑方向的误差，这是另外一种损失）。表示形式及导数如下：

$$\begin{gathered} L_1=|f(x)-Y| \\ {L}_1^{{}^{\prime }}=\pm f^{{}^{\prime }}(x)\text{\hspace{1em}(1)} \end{gathered}$$
对其进行求和，即为总的loss:

$$L_1=\sum _i^n|f(x_i)-Y_i|\text{\hspace{1em}(2)}$$

本文为简单，后面的描述未采用求和的形式进行表示。

优点：无论对于什么样的输入值，都有着稳定的梯度，不会导致梯度爆炸问题，具有较为稳健的解
缺点：在中心点是折点，不能求导，不方便求解，可能影响收敛

L2 Loss

也就是L2 Loss了，它有几个别称：

• L2 范数损失
• 最小均方值偏差（LSD）
• 最小均方值误差（LSE）
  最常看到的MSE也是指L2 Loss损失函数,区别在于MSE对loss进行了平均（mean,1/n）操作

它是把期望值Y 与模型输出值（预测值）f(x)求差然后平方得到的误差。表示形式及导数如下：
$$\begin{gathered} L_2=|f(x)-Y{|}^2 \\ {L}_2^{{}^{\prime }}=2f^{{}^{\prime }}(x)f(x)\text{\hspace{1em}(3)} \end{gathered}$$
观察图1中L2 loss的误差分布曲线，其中最小值为预测值等于目标值的位置。可以看到，随着误差的增加，损失函数增加的更为迅猛。
优点：各点都连续光滑，方便求导，具有较为稳定的解
缺点：不是特别的稳定（因为当模型输出与期望值相差较大的时候，使用梯度下降法求解的时候梯度很大，可能导致梯度爆炸）

L1 loss 和L2 loss比较

如下表1所示：

L2损失函数	L1损失函数
不是非常的鲁棒(robust)	鲁棒
稳定解	不稳定解

所谓“鲁棒性”，是指控制系统在一定（结构，大小）的参数摄动下，维持其它某些性能的特性。
所谓“稳定性”，是指控制系统在使它偏离平衡状态的扰动作用消失后，返回原来平衡状态的能力。

• 鲁棒性的分析：
  L1损失函数采用的方法之所以是鲁棒的，是因为它能处理数据中的异常值。从直观上说，因为L2范数将误差平方化（如果误差大于1，由于平方作用，误差会被放大很多），模型的误差会比L1范数来得大，因此模型会对这个样本更加敏感，这就需要调整模型来最小化误差。如果这个样本是一个异常值，模型就需要调整以适应单个的异常值（模型会赋予异常点更大的权重），这会牺牲许多其它正常的样本，因为这些正常样本的误差比这单个的异常值的误差小，这样模型会以牺牲其他样本的误差为代价，朝着减小异常点误差的方向更新，这将降低模型的整体性能。

• 稳定性的分析：
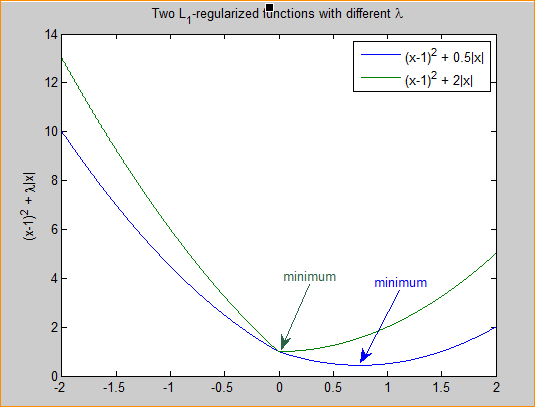
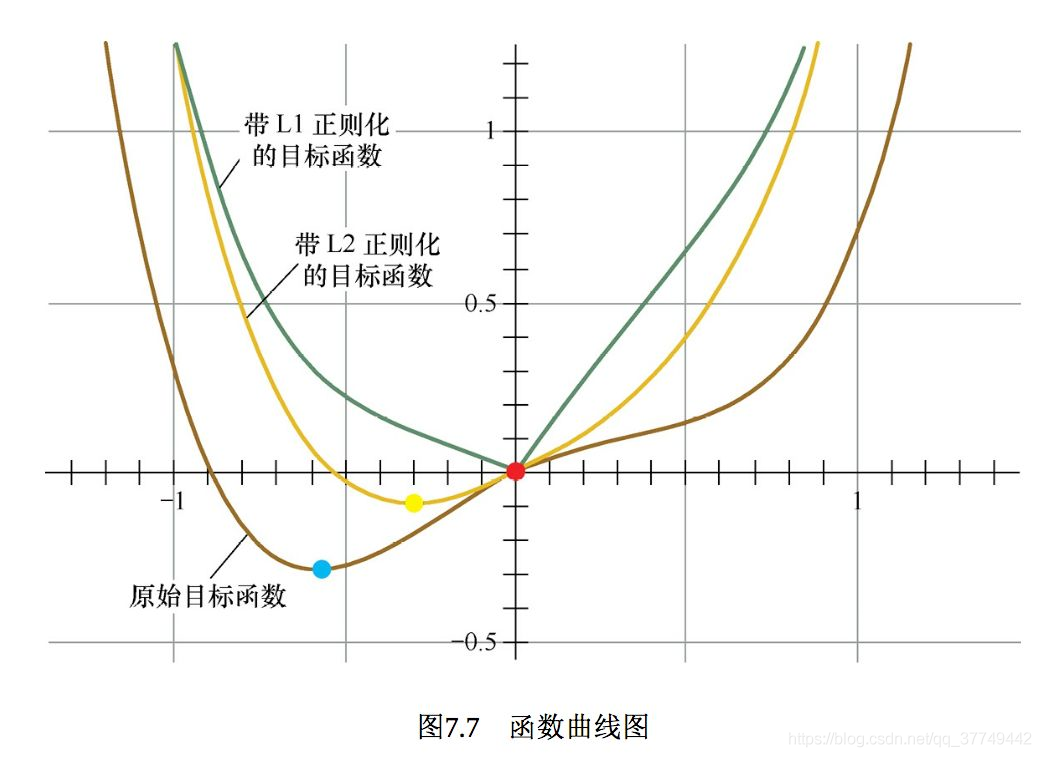
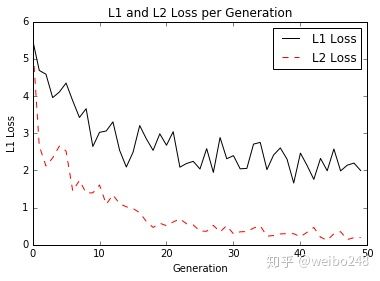
  该原因来源于L1 loss更新的梯度始终相同，也就是说，即使对于很小的损失值，梯度也很大。这样不利于模型的学习。L2 loss在这种情况下的表现就很好，即便使用固定的学习率也可以有效收敛。L2 loss的梯度随损失增大而增大，而损失趋于0时则会减小。这使得在训练结束时，使用L2 loss模型的结果会更精确。如下图所示
  

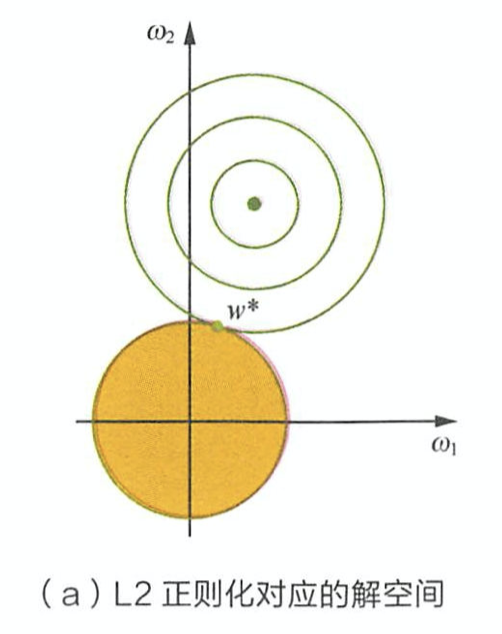
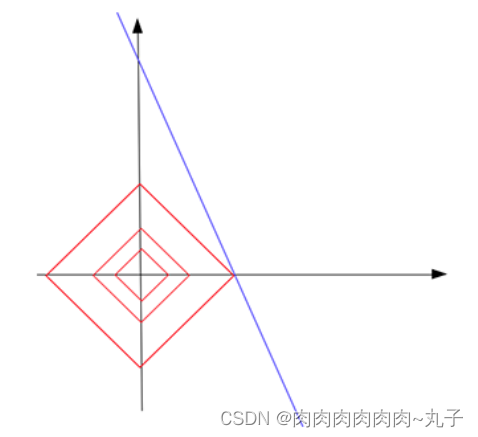
  L1损失函数采用的方法不稳定性意味着，对于数据集的一个小的水平方向的波动，回归线也许会跳跃很大。在一些数据结构（data configurations）上，该方法有许多连续解；但是，对数据集的一个微小移动，就会跳过某个数据结构在一定区域内的许多连续解。（The method has continuous solutions for some data configurations; however, by moving a datum a small amount, one could “jump past” a configuration which has multiple solutions that span a region. ）在跳过这个区域内的解后，L1 loss偏差线可能会比之前的线有更大的倾斜。相反地，L2 loss的解是稳定的，因为对于一个数据点的任何微小波动，回归线总是只会发生轻微移动；也就说，回归参数是数据集的连续函数。

  为了解决L1 loss不稳定这个缺陷，我们可以使用变化的学习率，在损失接近最小值时降低学习率

• 选择：
  对于大多数CNN网络，我们一般是使用L2-loss而不是L1-loss，因为L2-loss的收敛速度要比L1-loss要快得多。
  

  对于边框预测回归问题，通常也可以选择平方损失函数（L2损失），但L2范数的缺点是当存在离群点（outliers)的时候，这些点会占loss的主要组成部分。比如说真实值为1，预测10次，有一次预测值为1000，其余次的预测值为1左右，显然loss值主要由1000主宰。所以FastRCNN采用稍微缓和一点绝对损失函数（smooth L1损失），它是随着误差线性增长，而不是平方增长。

• 共同存在的问题：
  二者兼有的问题是：在某些情况下，上述两种损失函数都不能满足需求。例如，若数据中90%的样本对应的目标值为150，剩下10%在0到30之间。那么使用L1 loss的模型可能会忽视10%的异常点，而对所有样本的预测值都为150。
  这是因为模型会按中位数来预测。而使用L2 loss的模型则会给出很多介于0到30的预测值，因为模型会向异常点偏移。

Smooth L1 Loss

简单来说就是平滑版的L1 Loss。
smooth L1 loss和L1 loss函数的区别在于，L1 loss在0点处导数不唯一，可能影响收敛。smooth L1 loss的解决办法是在0点附近使用平方函数使得它更加平滑。
函数表达式及导数如下：
$$\begin{gathered} smooth{L}_1=\{\begin{array}{ll}0.5\ast x^2& if|x|<1\\ |x|-0.5& otherwise\end{array} \\ smooth{L}_1^{{}^{\prime }}=\{\begin{array}{ll}x& if|x|<1\\ -1& x<-1\\ 1& x>1\end{array}\text{\hspace{1em}(4)} \end{gathered}$$
损失函数曲线见图1.
仔细观察可以看到，当预测值和ground truth差别较小的时候（绝对值差小于1），其实使用的是L2 Loss；而当差别大的时候，是L1 Loss的平移。Soooth L1 Loss其实是L2Loss和L1Loss的结合，它同时拥有L2 Loss和L1 Loss的部分优点。

• 当预测值和ground truth差别较小的时候（绝对值差小于1），梯度不至于太大。（损失函数相较L1 Loss比较圆滑）
• 当差别大的时候，梯度值足够小（较稳定，不容易梯度爆炸，解决了离群点的梯度爆炸问题）。

总结

对于L2 Loss： 当 x 增大时 L2 损失对 x 的导数也增大。这就导致训练初期，预测值与 groud truth 差异过于大时，损失函数对预测值的梯度十分大，训练不稳定。从 L2 Loss的梯度包含 (f(x) - Y)，当预测值 f(x) 与目标值 Y 相差很大时（此时可能是离群点、异常值(outliers)），容易产生梯度爆炸

对于L1 Loss： 根据方程 (1)，L1 对 x 的导数为常数。这就导致训练后期，预测值与 ground truth 差异很小时， L1 损失对预测值的导数的绝对值仍然为 1，而 learning rate 如果不变，损失函数将在稳定值附近波动，难以继续收敛以达到更高精度

对 smooth L1 loss： smooth L1 在x较小时，对x的梯度也会变小，而在x很大时，对x的梯度的绝对值达到上限 1，也不会太大以至于破坏网络参数。smooth L1 loss在 |x| >1的部分采用了 L1 loss，当预测值和目标值差值很大时, 原先L2梯度里的 (f(x) - Y) 被替换成了 ±1,，这样就避免了梯度爆炸, 也就是它更加健壮。smooth L1 完美地避开了 L1 和 L2 损失的缺陷。

smooth L1 loss让loss function对于离群点更加鲁棒，即：相比于L2损失函数，其对离群点/异常值（outlier）不敏感，梯度变化相对更小，训练时不容易跑飞

附：图1绘图代码

#!/usr/bin/env python3
#coding=utf-8#============================#
#Program:plotFunc.py
#       
#Date:19-12-3
#Author:liheng
#Version:V1.0
#============================#import matplotlib.pyplot as plt
import numpy as np# import matplotlib.font_manager as fm
# # 使用Matplotlib的字体管理器加载中文字体
# my_font=fm.FontProperties(fname="C:\Windows\Fonts\simkai.ttf")# 支持中文
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['AR PL UKai CN'] #matplotlib中自带的中文字体
#解决负号'-'显示为方块的问题
plt.rcParams['axes.unicode_minus']=Falsex_data = np.arange(-2.0,2.0,0.01)L1_loss = np.abs(x_data)
L2_loss = np.square(x_data)
smooth_L1_loss = 0.5*np.square(x_data)*(np.abs(x_data)<1) + (np.abs(x_data)-0.5)*(np.abs(x_data)>=1)x_data_ex = np.arange(-1.0,1.0,0.01)
smooth_L1_loss_ext = (np.abs(x_data_ex)-0.5)*(np.abs(x_data_ex)<=1)# 指定折线的颜色、线宽和样式
ln2, = plt.plot(x_data, L2_loss, color = 'blue', linewidth = 2.0, linestyle = '-',label='L2 loss')
ln1, = plt.plot(x_data, L1_loss, color = 'red', linewidth = 2.0, linestyle = '-',label='L1 loss')
ln3, = plt.plot(x_data, smooth_L1_loss, color = 'green', linewidth = 2.0, linestyle = '-',label='smooth_L1_loss')
ln4, = plt.plot(x_data_ex, smooth_L1_loss_ext, color = 'green', linewidth = 1.0, linestyle = ':')plt.xlim([-2,2])
plt.ylabel('loss value')
plt.grid(linestyle='-.')plt.scatter(1,0.5,s=80,color='red')
plt.scatter(-1,0.5,s=80,color='red')# 调用legend函数设置图例
# plt.legend(loc='lower right', prop=my_font)
plt.legend(loc='upper right')
# 调用show()函数显示图形
plt.show()# from matplotlib.font_manager import FontManager
# import subprocess
#
# mpl_fonts = set(f.name for f in FontManager().ttflist)
# print('all font list get from matplotlib.font_manager:')
# for f in sorted(mpl_fonts):
#     print('\t' + f)
# output = subprocess.check_output('fc-list :lang=zh -f "%{family}\n"', shell=True, encoding="utf8")
# zh_fonts = set(f.split(',', 1)[0] for f in output.split('\n'))
#
# print('\n' + 'Chinese font list get from fc-list:')
# for f in sorted(zh_fonts):
#     print('\t' + f)
# print('\n' + 'the fonts we can use:')
# available = set(mpl_fonts) & set(zh_fonts)
# for f in available:
#     print('\t' + f)

参考资料

1.【学习】L1 loss 和 L2 loss
2.【机器学习】L1 loss & L2 loss & Smooth L1 loss
3.PyTorch中的损失函数–L1Loss /L2Loss/SmoothL1Loss
4.MSE与MAE的区别与选择
5.详解L1、L2、smooth L1三类损失函数
6.为什么Faster-rcnn、SSD中使用Smooth L1 Loss 而不用Smooth L2 Loss

---

下面的是我的公众号二维码图片，欢迎关注。