L1/L2范数

文中内容为一下博文整理而来
https://blog.csdn.net/iterate7/article/details/75443504
https://blog.csdn.net/zhaomengszu/article/details/81537197

什么是范数

范数是具有“长度”概念的函数。在向量空间内，为所有的向量的赋予非零的增长度或者大小。不同的范数，所求的向量的长度或者大小是不同的。例如，2维空间中，向量(3,4)的长度是5，那么5就是这个向量的一个范数的值，更确切的说，是欧式范数或者L2范数的值。

要更好地理解范数，就要从函数、几何、与矩阵的角度去理解。函数与几何图形往往有对应关系，在三维以下的空间内，函数是几何图像的数学概括，而几何图像是函数的高度形象化，如 $f (x) = x$ 就是一条直线。但当函数与几何超出三维空间时，人就难以获得较好的想象，于是就有了映射的概念，映射表达的就是一个集合通过某种关系转为另一个集合。通常数学书是先说映射，然后再讨论函数，这是因为函数是映射的一个特例。为了更好地在数学上表达这种映射关系，（这里特指线性关系）于是就引进了矩阵。这里的矩阵就是表征上述空间映射的线性关系。矩阵就是某种关系的集中表达。

于是，我们可以这样理解，一个集合（向量），通过一种映射关系（矩阵），得到另一个集合（向量）。那么向量的范数就是表示这个原有集合的大小，比如维度。而矩阵的范数，就是表示这个变化过程的大小的一个度量。范数就是度量向量的变化程度，那么具体的几几范数，其不过是定义不同。

而具体的用法，在计算机领域，用的比较多的就是迭代过程中收敛性质的判断，如果理解上述的意义，在计算机领域，一般迭代前后步骤的差值的范数表示其大小，常用的是二范数，差值越小表示越逼近实际值，可以认为达到要求的精度，收敛。

对于p-范数，如果 $x = [x_1,x_2,...,x_n]$ ,那么向量 $x$ 的p-范数就是：
$||X||_p=(|x_1|^p + |x_2|^p + ....+|x_n|^p)^{\frac{1}{p}}$
在应用中，用的最多的还是L1，L2范数。

L1范数，为绝对值之和： $X||_1 = (|x_1| + |x_2| + ... + |x_n|)$
L2范数，即欧式距离： $||X||_2 = (|x_1|^2 + |x_2|^2 + ... + |x_n|^2)^{\frac12}$
L0范数：指向量中非0元素的个数。无穷范数：指向量中元素绝对值中的最大值。

机器学习中的L1/L2:

机器学习中几乎都可以看到损失函数后面会添加一个额外项，常用的额外项一般有两种， $l_1-norm$ 和 $l_2-norm$ ，即L1正则化和L2正则化，或者L1、L2范数。

L1、L2正则化可以看做是损失函数的惩罚项。所谓惩罚，是指对损失函数中的某些参数做一些限制。对于线性回归模型，使用L1正则化的模型叫做Lasso回归，使用L2正则化的模型叫做Ridge回归。
L2正则的优化目标公式：
$\frac12\lambda\sum_iw_i^2$
L1正则的优化目标公式：
$\lambda \sum_i |w_i|$

也有以下的形式：
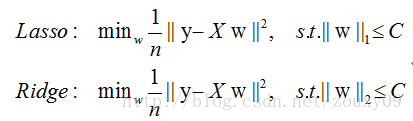
在这里插入图片描述
L1正则化和L2正则化的作用：

L1正则可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择
L2正则可以防止模型过拟合（overfitting），一定程度上，L1也可以防止过拟合

L1和L2，一个是让绝对值最小，一个让平方最小，有什么差别？

下降速度：L1和L2都是规则化的方式，我们将权值参数以L1或者L2的方式放到代价函数中，然后模型就会尝试去最小化这些权值参数。而这个最小化就像一个下坡的过程，L1和L2的差别就在于这个“坡”不同，如下图，L1就是按绝对值函数的“坡”下降的，而L2是按二次函数的“坡”下降，所以在0附近根据其梯度，L1的下降速度比L2的下降速度要快。

在这里插入图片描述

接下来看看这个经典的图：
在这里插入图片描述
这张图展示了损失函数和正则函数之间的关系。从图中可以看出，假设损失函数的主体是一个凸函数，它的等高线均匀地向外扩散。在正方形L1的正则约束下，目标函数的最优解更容易出现在坐标轴上，这样的参数在有些坐标轴上为0，因此最优参数也就具有稀疏性。而圆形的L2正则就不太容易达到这个效果，从图上看最优参数不会落在坐标轴上，因此它也不容易获得稀疏性。所以：针对L1正则优化可以达到参数稀疏化的效果。
但是，以上的例子为凸函数，非凸函数比较复杂，优化曲面上分布着许多局部最优解，即使模型有在L1正则的约束，参数的优化结果还是有可能不落在坐标轴上，所以自然有可能得不到稀疏的效果。

上面提到L1正则化有助于生成一个稀疏权值矩阵，进而可以用于特征选择，那么为什么需要生成一个稀疏权值矩阵呢？

首先，什么是稀疏矩阵：稀疏矩阵指的是很多元素为0，只有少数元素是非0值的矩阵，即得到的模型的大部分系数都是0。
通常机器学习中特征数量很多，例如文本处理时，如果将一个词组（term）作为一个特征，那么特征数量会达到上万个（bigram）。在预测或分类时，那么多特征显然难以选择，但是如果带入这些特征得到的模型是一个稀疏模型，表示只有少数特征对这个模型有贡献，绝大部分特征是没有贡献的，或者贡献微小（因为它们前面的系数是0或者是很小的值，即使去掉对模型也没有什么影响），此时我们就可以只关注系数是非0值的特征。这就是系数模型与特征选择的关系。

参数稀疏能带来什么好处，再从参数存储和模型计算两个方面考虑：

参数稀疏化后模型需要存储的参数变少了，因此如果稀疏性足够强，采用稀疏矩阵的方式存储，模型需要的空间会变小
如果用cpu进行运算，由于有大量的参数不需要计算，利用一些稀疏矩阵的计算方式，模型的计算会更快。如果采用GPU计算，稀疏性并不能减少模型计算的时间

为什么L1正则化可以产生稀疏模型（L1是怎么让系数等于0的），以及为什么L2正则化可以防止过拟合？

假设有如下带L1正则化的损失函数：

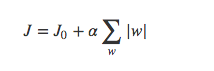
其中 $J_0$ 是原始的损失函数，后面的为L1正则化项， $\alpha$ 是正则化系数。注意到，L1正则化是权值的绝对值之和， $J$ 是带有绝对值符号的函数，因此 $J$ 是不完全可微的。机器学习的任务就是要通过一些方法（例如梯度下降）求出损失函数的最小值。当我们在原始损失函数 $J_0$ 后添加L1正则化项时，相当于对 $J_0$ 做了一个约束。令 $\alpha \sum_w |W|$ ，则 $J = J_0 + L$ ，此时我们的任务变成在 $L$ 约束下求出 $J_0$ 取最小值的解。考虑二维的情况，即只有两个权值 $w^1$ 和 $w^2$ ，此时 $L = |w^1| + |w^2|$ 对于梯度下降法，求解 $J_0$ 的过程可以画出等值线，同时L1正则化的函数 $L$ 也可以在 $w^1 w^2$ 的二维平面上画出来。如下：

上面等值线是 $J_0$ 的等值线，黑色方形是L函数的图形。在图中，当 $J_0$ 等值线与L图形首次相交的地方就是最优解。注意到这个定点的值是(w1,w2)=(0,w)(w1,w2)=(0,w)。可以直观想象，因为L函数有很多突出的角（二维情况下四个，多维情况下更多）， $J_0$ 与这些角接触的几率会远大于与L其它部位接触的几率，而在这些角上，会有很多权值为0，这就是为什么L1正则化可以产生稀疏模型，进而可以用于特征选择。

而正则化前面的系数 $\alpha$ ，可以控制L图形的大小。 $\alpha$ 越小，L的图形越大（上图中的黑色方框）， $\alpha$ 越大，L的图形就越小，可以小到黑色方框只超出原点范围一点点，这就是最优点的值(w1,w2)=(0,w)，其中的w可以取很小的值。

类似，假设有如下带L2正则化的损失函数:

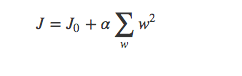
在这里插入图片描述
同样可以画出它们在二维平面的图形，如下：

在这里插入图片描述
二维平面下L2正则化的函数图形是个圆，与方形相比，被磨去了棱角。因此 $J_0$ 与 $L$ 相交时使得 $w^1$ 或者 $w^2$ 等于0的机率小了许多，这就是为什么L2正则化不具有稀疏性的原因。

拟合过程中，通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下，对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，即抗扰动能力强。

那么为什么L2正则化可以获得值很小的参数？

以线性回归中的梯度下降法为例。假设要求的参数为 $\theta$ ， $h_{\theta}(x)$ 是我们的假设函数，那么线性回归的代价函数如下：
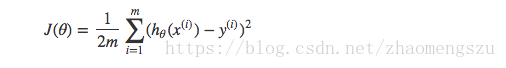
在这里插入图片描述
那么在梯度下降法中，最终用于迭代计算参数 $\theta$ 的迭代式为：

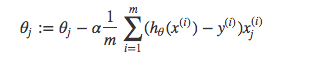
其中 $\alpha$ 为学习率。上式是没有添加L2正则化项的迭代公式，如果在原始代价函数之后添加L2正则化，则迭代公式会变成下面的样子：
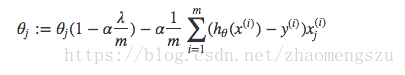
在这里插入图片描述
其中 $\lambda$ 就是正则化参数。从上式可以看到，与未添加L2正则化的迭代公式相比，每一次迭代， $\theta_j$ 都要先乘以一个小于1的因子，从而使得 $\theta_j$ 不断减小，因此总的来看， $\theta$ 是不断减小的。

之前有提到，L1正则化一定程度上也可以防止过拟合。当L1的正则化系数很小时，得到的最优解会很小，可以达到和L2正则化类似的效果。

正则化参数的选择

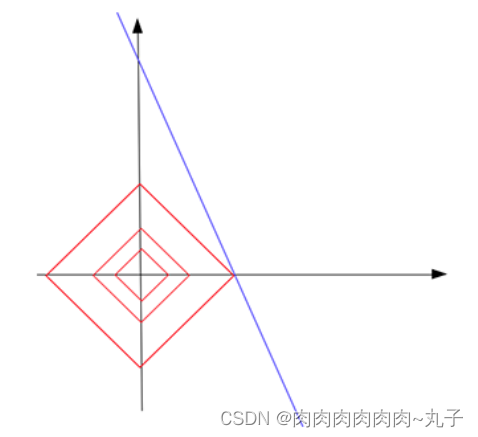
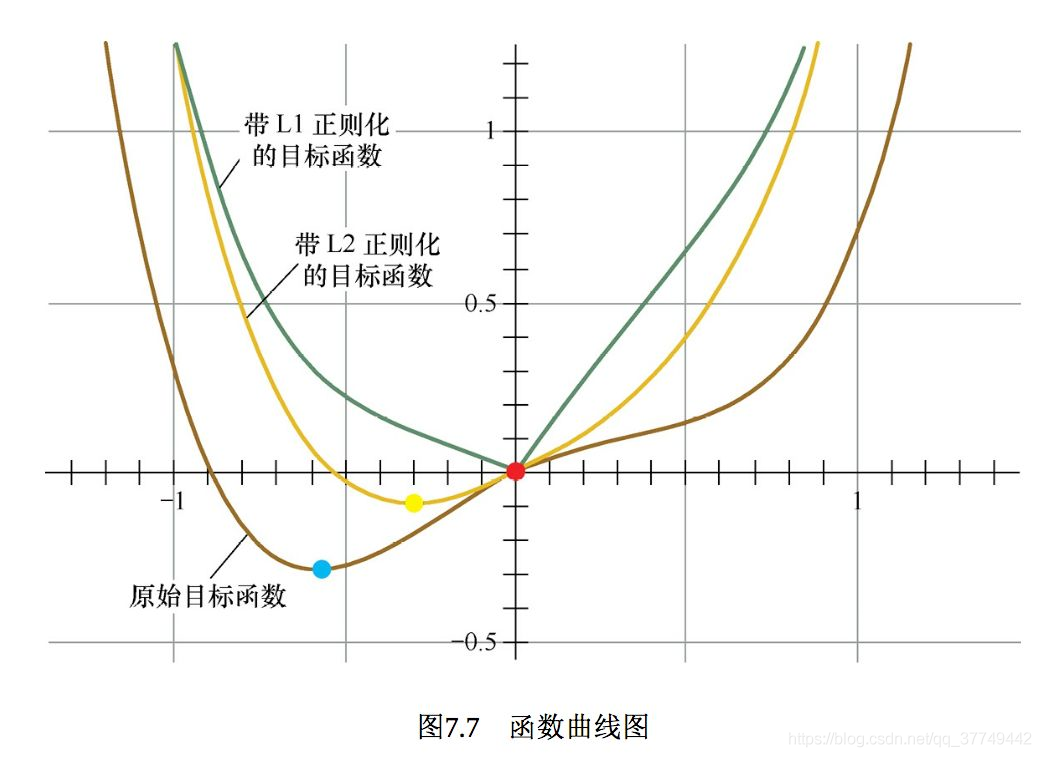
通常越大的 $\lambda$ 可以让代价函数在参数为0时取得最小值。下面是一个简单的例子，这个例子来自Quora上的问答。

假设有如下带L1正则化项的代价函数：
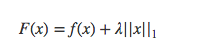
在这里插入图片描述
其中 $x$ 是要估计的参数，相当于上文中提到的 $w$ 以及 $\theta$ 。注意到L1正则化在某些位置是不可导的，当 $\lambda$ 足够大时可以使得 $F (x)$ 在 $x = 0$ 时取得最小值。

分别取 $\lambda=0.5$ 和 $\lambda=2$ ，可以看到越大的 $\lambda$ 越容易使F(x)在x=0时取得最小值。