原文链接: http://chenhao.space/post/b190d0eb.html

L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择。

所谓稀疏模型就是模型中很多的参数是0，这就相当于进行了一次特征选择，只留下了一些比较重要的特征，提高模型的泛化能力，降低过拟合的可能。

那么问题来了，为什么L1正则化会产生稀疏解？

L1/L2正则化损失函数

线性回归L1正则化损失函数：
$$\underset{w}{\min }[\sum _{i=1}^N(w^T{x}_i-y_i{)}^2+\lambda \Vert w{\Vert }_1]........(1)$$
线性回归L2正则化损失函数：
$$\underset{w}{\min }[\sum _{i=1}^N(w^T{x}_i-y_i{)}^2+\lambda \Vert w{\Vert }_2^2]........(2)$$

正则化作用

L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择。

L2正则化可以防止模型过拟合，一定程度上，L1也可以防止过拟合。

L1正则化与稀疏性

事实上，”带正则项”和“带约束条件”是等价的。为了约束 $w$ 的可能取值空间从而防止过拟合，我们为该优化问题加上一个约束，就是 $w$ 的L1范数不能大于m：

$$\{\begin{array}{l}\min {\sum }_{i=1}^N(w^T{x}_i-y_i{)}^2\\ s.t.\Vert w{\Vert }_1⩽m.\end{array}........(3)$$

$(1)$式和$(3)$式是等价的，为了求解带约束条件的凸优化问题，写出拉格朗日函数：

$$\sum _{i=1}^N(w^T{x}_i-y_i{)}^2+\lambda (\Vert w{\Vert }_1-m)........(4)$$

设 $w^{\ast }$ 和 ${\lambda }^{\ast }$ 是原问题和对偶问题的最优解，则根据???条件得：

$$\{\begin{array}{l}0={\nabla }_w[{\sum }_{i=1}^N(W^{\ast T}{x}_i-y_i{)}^2+{\lambda }^{\ast }(\Vert w{\Vert }_1-m)]\\ 0⩽{\lambda }^{\ast }.\end{array}........(5)$$

$(5)$式中的第一个式子不就是 $w^{\ast }$ 为带 L2 正则项的优化问题的最优解的条件嘛，而 ${\lambda }^{\ast }$ 就是L2正则项前面的正则参数。

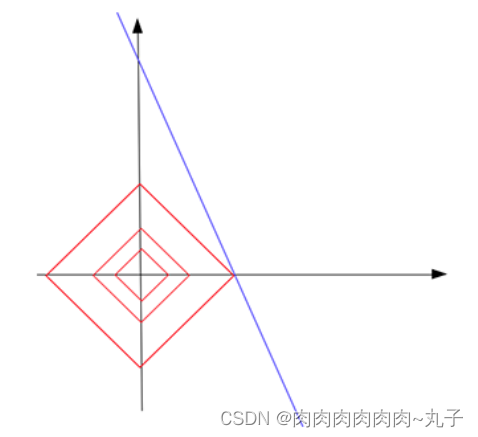
由上面公式推导可看出，L1正则项相当于为参数定义了一个棱形的解空间（因为必须保证L1范数不能大于m，L1范数的值又等于所有参数绝对值之和，即 $|w_1|+|w_2|+|w_3|+...+|w_n|⩽m$），假设参数为2个，即 $|w_1|+|w_2|⩽m$ ，我们画出它的解空间：

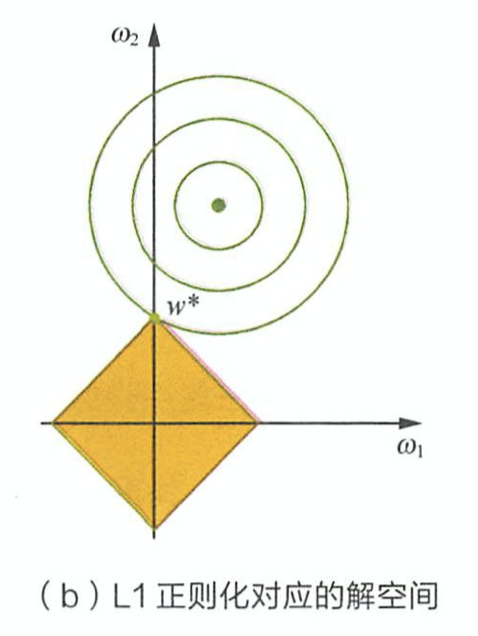
设L1正则化损失函数：$J=J_0+\lambda {\sum }_w|w|$ ，其中 $J_0={\sum }_{i=1}^N(w^T{x}_i-y_i{)}^2$ 是原始损失函数，后面那一项是L1正则化项，$\lambda$ 是正则化系数。图中的等线图就是 $J_0$ ，棱形是L1正则化项的解空间，当它们俩在某点处相交时，该点就是最优解。很明显，在棱形的解空间中，棱角顶点很容易与等线图相交。

在上图中，它们相交就意味中 $w_1$ 和 $w_2$ 至少有一个为0，当参数更多时也是同理。

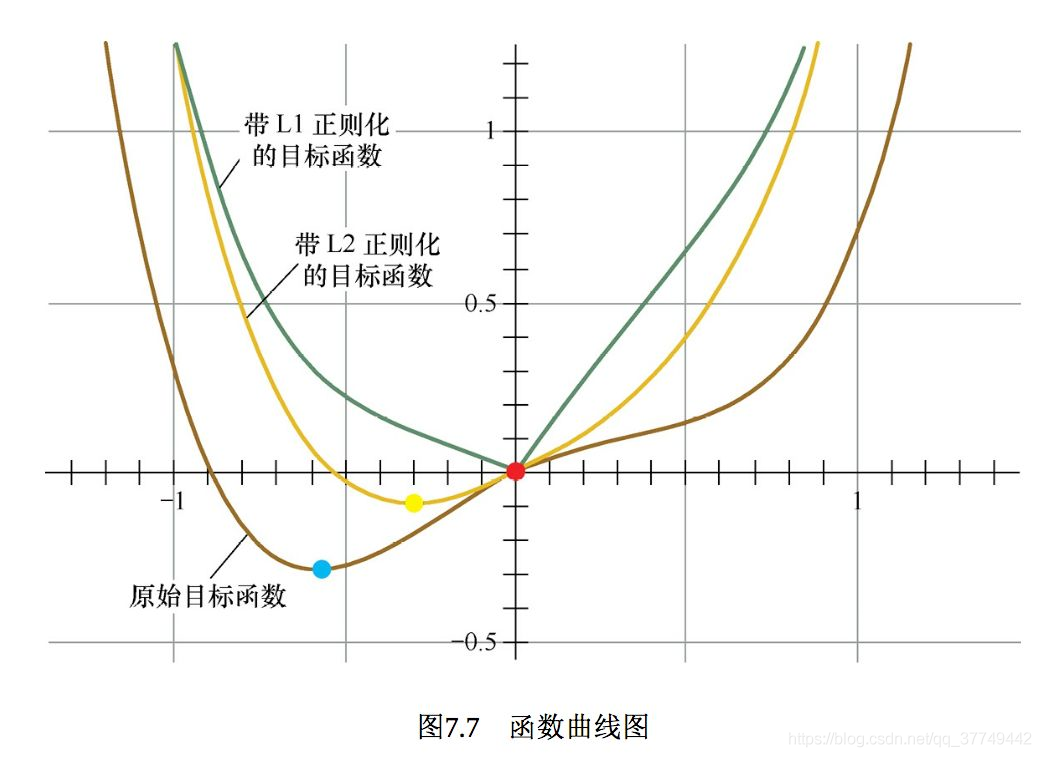
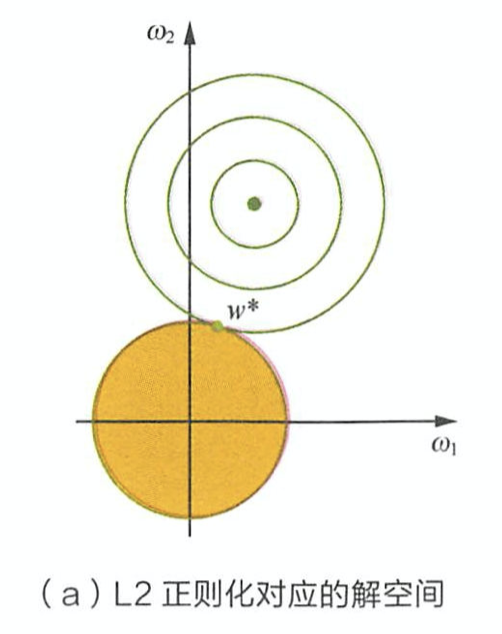
L2正则化的空间解如下图（公式推导跟L1差不多）：

参考资料

1. 百面机器学习
2. 深入理解L1、L2正则化