1.概述

drools是一个规则引擎,什么是规则引擎?就是能够自动将决策树转化为基本规则.这样的好处就是把决策规则从代码中摘出来,形成单独的规则文件.这样的好处有三个:
1.规则文件单独成册,可以编著多个规则文件进行归档管理,具有历史记忆的功能
2.规则文件可以支持修改,而不影响代码的结构,使得规则和代码解耦
3.规则文件可以被持久化,通过解析和破解

举个例子

当我们有一个业务逻辑,比如说是价格砍价行为
满100打8折
满200打7折
满300打6折
满400打5折
组合购物超过500送20优惠券
…
大概就是你在淘宝上看到的复杂的规则.那么针对这些问题,我们常规的做法是使用代码来实现,通过java将其嵌入到业务逻辑中,那么代码应该是这样:

		double price=0;double zhekou=0,youhui=0;if(price>100&&price<200){price=price*(1-zhekou);}else if(price>200&&price<300){price=price*(1-zhekou);}else if(price>100&&price<200){price=price*(1-zhekou);}...

那么像这种逻辑,我们就不说他丑了,他存在的最大的问题有两个:
1.当打折力度变化时需要深入到代码中,定位到具体的行来进行参数修改
2.但凡规则变了,就要整体修改业务逻辑的代码,比如加入了一个新的优惠规则
为了解决这样的问题,drools发挥了很好的作用,他的效果大概是这样的图示:
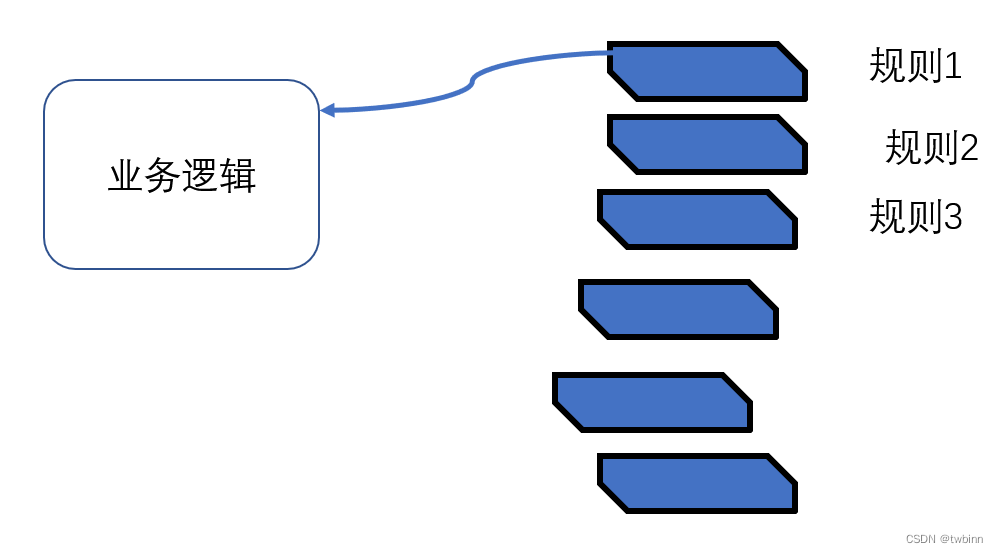
可切换的规则
drools用这种方式,能够实现不更改业务逻辑的前提下,主动切换规则.
接下来本文就进行实践,说明drools如何引入maven和spirngboot中

2.结合maven引入

1.引入maven

首先需要在maven中引入drools的依赖,drools要引入的依赖有几个,分别是drools-compiler,drools-bom,kie-api.引入的pom大概长这样:

<dependency><groupId>org.drools</groupId><artifactId>drools-compiler</artifactId><version>7.29.0.Final</version></dependency><!-- https://mvnrepository.com/artifact/org.kie/kie-api --><dependency><groupId>org.kie</groupId><artifactId>kie-api</artifactId><version>7.29.0.Final</version></dependency><dependency><groupId>org.drools</groupId><artifactId>drools-bom</artifactId><type>pom</type><version>7.69.0.Final</version><scope>import</scope></dependency>

需要注意drools的版本和各个插件之间的依赖版本的关系.
在引入drools的组件后,就能在spirng项目中进行测试了.
首先在Resources文件夹下建立META-INF文件件和rules文件夹

2.创建kmoudule.xml文件

在META-INF文件夹下建立kmodule.xml文件,输入以下内容:

<?xml version="1.0" encoding="UTF-8"?>
<kmodule xmlns="http://jboss.org/kie/6.0.0/kmodule"><kbase name="personal" packages="rules"><ksession name="PersonalRulePackage" /></kbase>
</kmodule>

对上述参数做简要说明,其中kbase name是容器的参数,ksession name是会话的参数,这两个参数在后续编写drools的规则控制的时候需要用到.
然后在rules文件夹下面建立一个drl文件,这个文件就是drools的主体的规则文件.
对于idea没有drl插件的问题,要在插件管理中心安装drools插件.但是我在安装的时候,查检中心并没有这个插件.我的方式是手动去idea的仓库,下载drools的插件,然后通过本地磁盘安装的方式,实现对drools插件的安装.

3如有需要,安装drools的插件

在这里插入图片描述

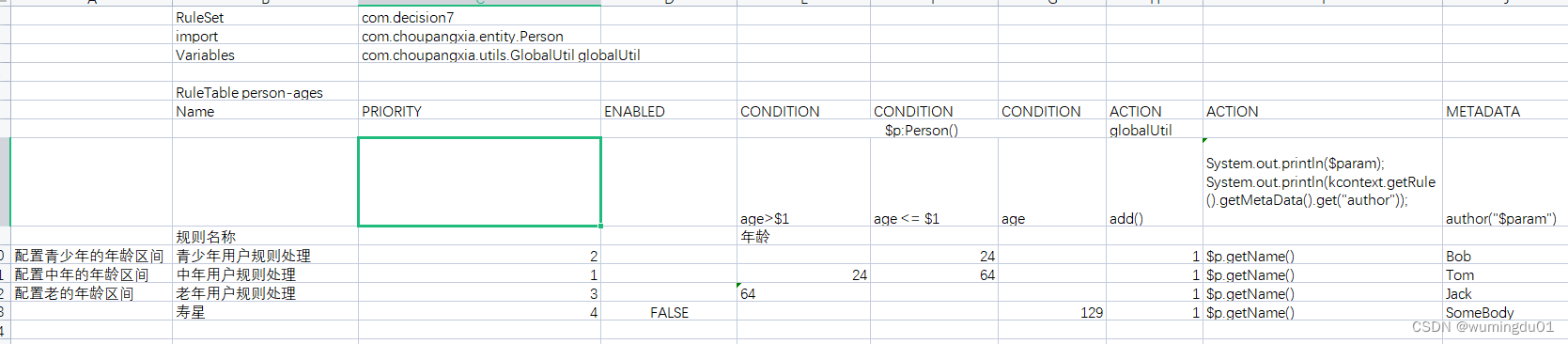
4编写drl规则文件

在安装好以后,就能比较好的支持drl文件的编写了.下面首先写一个简单的drl文件,类似于drools领域的hello world

import com.entity.Persondialect  "mvel"
rule "test_01"
when$p:Person($x:age>10)
thenSystem.out.println("加上80");
end

5准备用于测试的po类

现在对上述的规则进行说明,其中的person是我自己写的测试类,下面是person的数据结构:

public class Person {String name;int age;String sex;}

这个规则实现的是当person的age>10的时候,输出一句话.

6编写drools的java接口

下面要做的就是编写java的drools容器接口,来实现对容器的部署\会话的建立,规则的逻辑
下面是基本代码:

public static void main(String[] args) {KieServices kieServices = KieServices.Factory.get();KieContainer kieClasspathContainer = kieServices.getKieClasspathContainer();KieSession kieSession = kieClasspathContainer.newKieSession("PersonalRulePackage");Person zhangsan = new Person("zhangsan", 90);kieSession.insert(zhangsan);kieSession.fireAllRules();}