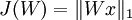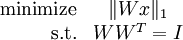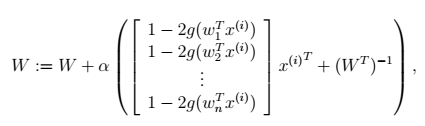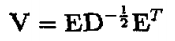独立成分分析
Contents[hide]
|
概述
试着回想一下，在介绍 稀疏编码算法中我们想为样本数据学习得到一个超完备基（over-complete basis）。具体来说，这意味着用稀疏编码学习得到的基向量之间不一定线性独立。尽管在某些情况下这已经满足需要，但有时我们仍然希望得到的是一组线性独立基。独立成分分析算法（ICA）正实现了这一点。而且，在 ICA 中，我们希望学习到的基不仅要线性独立，而且还是一组标准正交基。（一组标准正交基 
需要满足条件：
（如果
）或者
（如果i = j））
与稀疏编码算法类似，独立成分分析也有一个简单的数学形式。给定数据 x，我们希望学习得到一组基向量――以列向量形式构成的矩阵 W，其满足以下特点：首先，与稀疏编码一样，特征是稀疏的；其次，基是标准正交的（注意，在稀疏编码中，矩阵 A 用于将特征 s 映射到原始数据，而在独立成分分析中，矩阵W 工作的方向相反，是将原始数据 x 映射到特征）。这样我们得到以下目标函数：
由于 Wx 实际上是描述样本数据的特征，这个目标函数等价于在稀疏编码中特征 s 的稀疏惩罚项。加入标准正交性约束后，独立成分分析相当于求解如下优化问题：
与深度学习中的通常情况一样，这个问题没有简单的解析解，而且更糟糕的是，由于标准正交性约束，使得用梯度下降方法来求解该问题变得更加困难――每次梯度下降迭代之后，必须将新的基映射回正交基空间中（以此保证正交性约束）。
实践中，在最优化目标函数的同时施加正交性约束（如下一节 正交ICA中讲到的）是可行的，但是速度慢。在标准正交基是不可或缺的情况下，标准正交ICA的使用会受到一些限制。（哪些情况见：TODO ）
标准正交ICA
标准正交ICA的目标函数是：
通过观察可知，约束WWT = I隐含着另外两个约束:
第一，因为要学习到一组标准正交基，所以基向量的个数必须小于输入数据的维度。具体来说，这意味着不能像通常在 稀疏编码中所做的那样来学习得到超完备基（over-complete bases）。
第二，数据必须经过无正则 ZCA白化（也即,ε设为0）。（为什么必须这样做？见TODO）
因此，在优化标准正交ICA目标函数之前，必须确保数据被白化过，并且学习的是一组不完备基（under-complete basis）。
然后，为了优化目标函数，我们可以使用梯度下降法，在梯度下降的每一步中增加投影步骤，以满足标准正交约束。过程如下：
重复以下步骤直到完成：
, 其中U是满足WWT = I的矩阵空间
在实际中,学习速率α是可变的,使用一个线搜索算法来加速梯度.投影步骤通过设置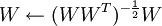
来完成,这实际上可以看成就是ZCA白化(TODO:解释为什么这就象ZCA白化).
拓扑ICA
与 稀疏编码算法类似，加上一个拓扑代价项，独立成分分析法可以修改成具有拓扑性质的算法。
中英文对照
- 独立成分分析 Independent Component Analysis
- 稀疏编码算法 Sparse coding
- 超完备基 Over-complete basis
- 标准正交基 Orthonormal basis
- 稀疏惩罚项 Sparsity penalty
- 梯度下降法 Gradient descent
- 白化 Whitened
- 不完备基 Under-complete basis
- 线搜索算法 Line-search algorithm
-
拓扑代价项 Topographic cost term
from: http://ufldl.stanford.edu/wiki/index.php/%E7%8B%AC%E7%AB%8B%E6%88%90%E5%88%86%E5%88%86%E6%9E%90
