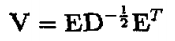学习笔记 | 独立成分分析[ICA, FastICA]及应用

1 背景说明
2 算法原理
- 2.1 ICA简介
- 2.2 形式化表达
3 算法步骤与代码
4 算法改进：FastICA
5 ICA实例与应用
6 小结

概要： 这篇博客和博客学习笔记|主成分分析[PCA]及其若干应用属于一个系列，介绍独立成分分析(Independent Component Analysis, ICA)的原理及简单应用。ICA也是一种矩阵分解算法，尽管它最开始不是基于此而提出来的。
关键字： 矩阵分解; 独立成分分析; ICA

1 背景说明

提到独立成分分析就不得不说著名的“鸡尾酒会问题”，如图1所示意。该问题描述的是一场鸡尾酒会中有N个人一起说话，同时有N个录音设备，问怎样根据这N个录音文件恢复出N个人的原始语音。鸡尾酒会问题也叫做盲源分离问题，ICA就是针对该问题所提出的一个算法。

图1 鸡尾酒会问题示意

2 算法原理

2.1 ICA简介

ICA原理在此不再赘述，这里给出一些博主认为质量高的文章链接。

这篇文章题为“说说鸡尾酒会问题(Cocktail Party Problem)和程序实现”，对ICA的原理作了简单描述，并且给出了一个实现代码；
这篇文章是作者斯坦福CS229机器学习个人总结系列文章中的一篇，将ICA与因子分析(Factor Analysis, FA)、主成分分析(Principal Component Analysis, PCA)放在一起进行比较，图文并茂、内容详实，而且有一系列文章可供参考；
这篇文章给出了ICA算法的可编程步骤，我的ICA代码就是参照这篇文章写的，同时作者也有一个关于CS229的学习心得系列值得一看；
CSDN博主沈子恒的系列文章(意义、概念、直观解释、最优估计、信息极大化、与PCA的差别1、与PCA的差别2)由浅入深地从多个角度介绍了ICA及其改进算法，对ICA研究的多个方向均有涉及。

除此以外，还有许多优秀的英文资料可供参考。

这是吴恩达CS229课程中关于ICA算法的英文原版教案；
这篇文章源于国外某个英文博主，从概率角度介绍了ICA算法并给出了一些实例；
这里给出了ICA及FastICA算法的教材链接和一个MATLAB代码工具包。

除此以外，还有各种教学网页和可视资源可以从YouTube、GitHub或其他网站上获取，这里不再罗列。

2.2 形式化表达

将一个问题通过数学方法表达出来，就是形式化表达，这是求解问题的第一步。本篇同样用PPT代劳，如图2所示。

图2 ICA算法的形式化表示

这就是ICA的形式化表示，对于一个输入的 $n$ 行 $m$ 列矩阵，ICA的目标就是找到一个 $n$ 行 $n$ 列混淆矩阵 $A$ ，使得变换后的矩阵仍为 $n$ 行 $m$ 列矩阵，但是每一行不再是多人说话的混合语音而是解混得到的某一个人的说话语音。

3 算法步骤与代码

经过中间一系列计算步骤(这里不一一展现)，最后得到了ICA算法的实现步骤如图3所示(仍然是PPT代劳)：

图3 ICA算法执行步骤

其中第3步提到的白化预处理步骤如图4所示，白化也是一个值得深入学习的概念，是数据处理中一个常用的重要方法，这里不细说。

图4 白化预处理步骤

有了步骤，接下来就只剩小学生都会做的编程了。

MATLAB代码如下：

function S = myICA(X)
%MYICM - The ICA(Independent Component Analysis) algorithm.
%   To seperate independent signals from a mixed matrix X, the unmixed
%   signals are saved as rows of matrix S.
%   Here are some useful reference material:
%   https://blog.csdn.net/YJJat1989/article/details/22593489
%   http://cnl.salk.edu/~tewon/Blind/blind_audio.html
%
%   S = myICA(X)
% 
%   Input - 
%   X: a N*M matrix with mixed signals containing M datas with N dimensions;
%   Output - 
%   S: a N*M matrix with unmixed signals.
% 
%   Copyright (c) 2018 CHEN Tianyang
%   more info contact: tychen@whu.edu.cn%% ICA calculation
if ~ismatrix(X)error('Error!');
end
[n,m] = size(X);
S = zeros(n,m);
W_old = rand(n);
for row = 1:nW_old(row,:) = W_old(row,:)/sum(W_old(row,:));
end
delta = 0.001;
itera = 1000;
alfa = 0.01;
for T = 1:mfor i = 1:iteraweight = zeros(n,1);for line = 1:nweight(line) = 1-2*sigmoid(W_old(line,:)*X(:,T));endW_new = W_old+alfa*( (weight(line)*(X(:,T))')+ inv(W_old') );if sum(sum(abs(W_new-W_old))) <= deltabreak;elseW_old = W_new;endendS(:,T) = W_new*X(:,T);
endend%% sigmoid function
%--------------------------------------------------------------------
function g = sigmoid(x)g = 1/(1+exp(-x));
end
%%

白化步骤的代码也顺便一起贴上，注意白化一般也分为PCA白化和ZCA白化，按需输出结果。

function Y = myWhite(X,DIM)
%MYWHITE - The whitening function.
%   To calculate the white matex of input matrix X and 
%   the result after X being whitened. 
%   
%   Res = myWhite(X,DIM)
% 
%   Input - 
%   X: a N*M matrix containing M datas with N dimensions;
%   DIM: specifies a dimension DIM to arrange X.
%       DIM = 1: X(N*M)
%       DIM = 2: X(M*N)
%       DIM = otherwisw: error
%   Output - 
%   Y  : result matrix of X after being whitened;
%       Y.PCAW: PCA whiten result;
%       Y.ZCAW: ZCA whiten result.
% 
%   Copyright (c) 2018 CHEN Tianyang
%   more info contact: tychen@whu.edu.cn%% parameter test
if nargin < 2DIM = 1;
end
if DIM == 2X = X';
elseif DIM~=1 && DIM~=2error('Error! Parameter DIM should be either 1 or 2.');
end
[~,M] = size(X);%% whitening
% step1 PCA pre-processing
X = X - repmat(mean(X,2),1,M);        % de-mean
C = 1/M*X*(X');                       % calculate cov(X), or: C = cov((X)')
[eigrnvector,eigenvalue] = eig(C);    % calculate eigenvalue, eigrnvector
% TEST NOW: eigrnvector*(eigrnvector)' should be identity matrix.
% step2 PCA whitening
if all(diag(eigenvalue))    % no zero eigenvalueXpcaw = eigenvalue^(-1/2) * (eigrnvector)' * X;
elsevari = 1./sqrt(diag(eigenvalue)+1e-5);Xpcaw = diag(vari) * (eigrnvector)' * X;
end
% Xpczw = (eigenvalue+diag(ones(size(X,1),1)*(1e-5)))^(-1/2)*(eigrnvector)'*X;    % 数据正则化
% step3 ZCA whitening
Xzcaw = eigrnvector*Xpcaw;
% TEST NOW: cov((Xpczw)') and cov((Xzcaw)') should be identity matrix.%% result output
Y.PCAW = Xpcaw;
Y.ZCAW = Xzcaw;end

4 算法改进：FastICA

事实上，ICA算法从提出至今就处于不断改进的进程中，到现在，经典的ICA算法已经基本不再使用，而是被一种名为FastICA的改进算法替代。顾名思义，该算法的优点在与Fast，即运算速度快。具体的改进点如图5所示。

图5 FastICA算法改进内容

经实测，改进后的算法的确比之前的ICA算法快了很多，且效果更佳。FastICA算法代码如下：

function Z = FastICA(X)
%FASTICA - The FastICA(Fast Independent Component Analysis) algorithm.
%   To seperate independent signals from a mixed matrix X, the unmixed
%   signals are saved as rows of matrix Z.
%   Here are some useful reference material:
%   https://blog.csdn.net/zf_suan/article/details/53750455
%
%   Z = FastICA(X)
% 
%   Input - 
%   X: a N*M matrix with mixed signals containing M datas with N dimensions;
%   Output - 
%   Z: a N*M matrix with unmixed signals.%% 去均值
[M,T]=size(X);   %获取输入矩阵的行列数，行数为观测数据的数目，列数为采样点数
average=mean((X'))';  %均值
for i=1:MX(i,:)=X(i,:)-average(i)*ones(1,T);
end%% 白化/球化
Y = myWhite(X,1);
Z = Y.PCAW;
% Z=X;
%% 迭代
Maxcount=10000;  %最大迭代次数
Critical=0.00001;  %判断是否收敛
m=M;            %需要估计的分量的个数
W=rand(m);
for n=1:mWP=W(:,n);  %初始权矢量（任意）%Y=WP'*Z;%G=Y.^3;%G为非线性函数，可取y^3等%GG=3*Y.^2；   %G的导数count=0;LastWP=zeros(m,1);W(:,n)=W(:,n)/norm(W(:,n));         %单位化一列向量while (abs(WP-LastWP) & abs(WP+LastWP)) > Critical    %两个绝对值同时大于收敛条件count=count+1;  %迭代次数LastWP=WP;      %上次迭代的值%WP=1/T*Z*((LastWP'*Z).^3)'-3*LastWP;for i=1:m%更新WP(i)=mean( Z(i,:).*(tanh((LastWP)'*Z)) )-(mean(1-(tanh((LastWP))'*Z).^2)).*LastWP(i);endWPP=zeros(m,1);     %施密特正交化for j=1:n-1WPP=WPP+(WP'*W(:,j))*W(:,j);endWP=WP-WPP;WP=WP/(norm(WP));if count==Maxcountfprintf('未找到相应的信号');return;endendW(:,n)=WP;
end%% 数据输出
Z=W'*Z;end
%%

5 ICA实例与应用

ICA算法原本就是针对盲源分离问题而提出的，现在就将其应用于该问题，测试它的效果。由于语音信号无法上传至CSDN，因此把处理前后的文件上传网络并提供下载链接，文件说明如下。

图6 实验文件

其中，“sound1.wav”和“sound2.wav”是2段清晰原始语音；“mixed1.wav”和“mixed2.wav”是2段由计算机上述两段语音混淆之后得到的语音；“icaunmixed1.wav”和“icaunmixed2.wav”是使用经典的ICA算法解混得到的结果；“ica_unmixed1_another.wav”和“ica_unmixed2_another.wav”是使用经典的ICA算法在另一组参数下得到的结果；“fastica_unmixed1”和“fastica_unmixed2.wav”是使用改进算法FastICA解混得到的结果。实验结果表明，FastICA耗时更短、效果更佳。