目录
一:连续信源
最大熵定理
二:渐进均分性
1:随机变量收敛性
2:大数定律
3:AEP(渐进均分性)
4:典型集
三:数据压缩
一:连续信源
1)连续随机变量的微分熵

由概率密度函数可知:被积函数和区间的积分表示的是发生的概率。![]()
由于:连续随机变量的取值是无限个,不确定性为无限大。确定输出某值的信息量也是无穷大,这里丢掉无穷大那一项,只取前面那个定值第一项,取名为微分熵。微分熵具有相对意义,比如比较两个连续随机变量不确定性的大小,由于无穷项被抵消,所以只讨论优先向是有意义的。
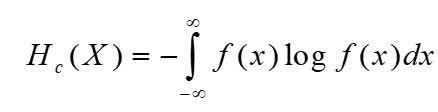
微分熵与离散熵的区别:
1: 微分熵去掉了无限项,不可以作为连续随机变量的真正不确定性的测量。
2:连续随机变量每一点取值为零,定义的自信息是无意义的,不能把微分熵视为:自信息量的统计平均。
连续随机变量的微分熵与绝对熵区别:

其他微分熵


记住:这个结论。
互信息:

最大熵定理

TH1:设X是取值受限于有限区间[a,b],则:X服从均匀分布时微分熵达到最大。(幅值受限)
TH2:设x均值为u,方差受限为,则X服从高斯分布时,熵值达最大。(方差受限)


二:渐进均分性
1:随机变量收敛性

随机变量序列收敛于一个随机变量有三种定义形式:依概率收敛,均方收敛,几乎处处收敛。
三种证明上都用到极限的语言。

2:大数定律

补充:i.i.d是独立同分布的意思,大数定律分为强大数定律和弱大数定律两种形式。

强大数定律想证明:采样的次数越多,平均值几乎一定越来接近真实期望值;
弱大数定律想证明:采样的次数越多,平均值接近真实期望值的可能性越来越大。
3:AEP(渐进均分性)

这一定理表明如果随机变量序列是独立同分布的,那么当序列的个数足够大时,它们的联合分布概率除以-n会趋近于它们的熵。而且也表明了它们的的总概率的和逐渐趋近于1。
变形:
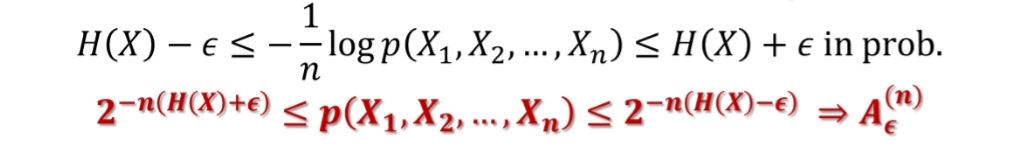
4:典型集


第2个结论说明:n足够大,典型集中的事件概率接近1,三四个结论给出典型集的元素个数上界和下界。
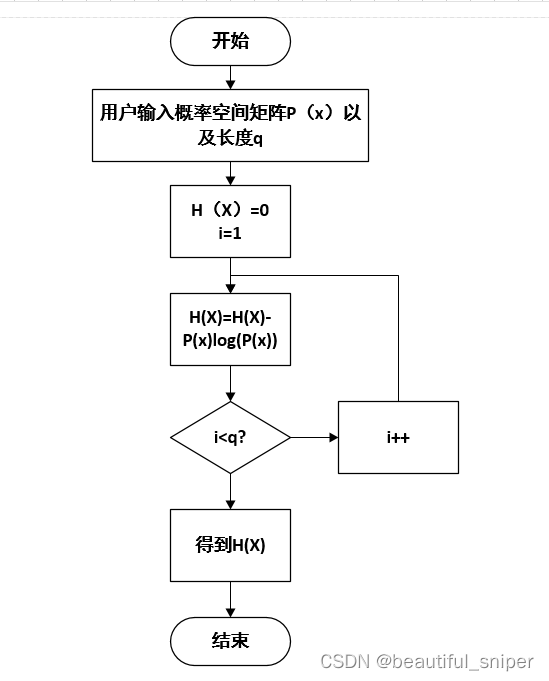
三:数据压缩

信源编码的核心:想要在误码率几乎为0的基础上(无损),使得信源编码的信息传输率尽可能小,也就是表示的码元符号少。
由于事件发生的概率不一样,所以可以不编码或者用多码字编码,而经常出现的概率大的事件要用马字短的编码。
编码方式:区分典型集和非典型集,然后在典型集前加0,非典型集前加1.




这个定理说明了:序列平均上最少用:nH(X)比特去表示。

如果:编码码率不能少于信源熵,那么不会存在一种正确的编码方式。
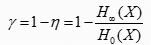



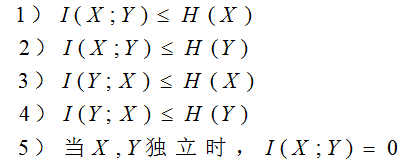
![[信息论与编码] 03. 离散信源、信源熵、联合熵、条件熵](https://img-blog.csdnimg.cn/20190605200610931.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxNzg1Mjg4,size_16,color_FFFFFF,t_70)