目录
1:熵的凸性
相对熵的下凸性
熵的上凸性
2:信源的分类
3:自信息
四:离散无记忆扩展信源
五:马尔科夫信源
六:马尔可夫信源的信源熵
求解方法
计算例子
1:熵的凸性
凸函数是定义在定义域为凸集的函数。
1:凸集的形象解释:我们在集合C中取任意两个元素,在这两个元素之间画一条直线,如果这条直线上的每一点都属于C,则集合C叫凸集。

2:上凸函数与下凸函数。

看突出的部分,向下凸就是下凸函数,向上凸就是上凸函数。
3:重要不等式

统计平均可以看成一个加权线性组合,利用下凸函数性质即可得到该不等式

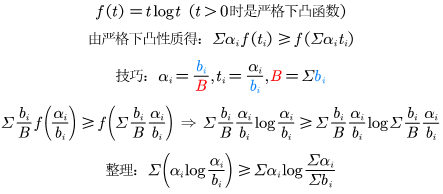
相对熵的下凸性

熵的上凸性
离散随机变量的熵与相对熵的关系:
这就好理解:常数+一个下凸函数的反=上凸函数
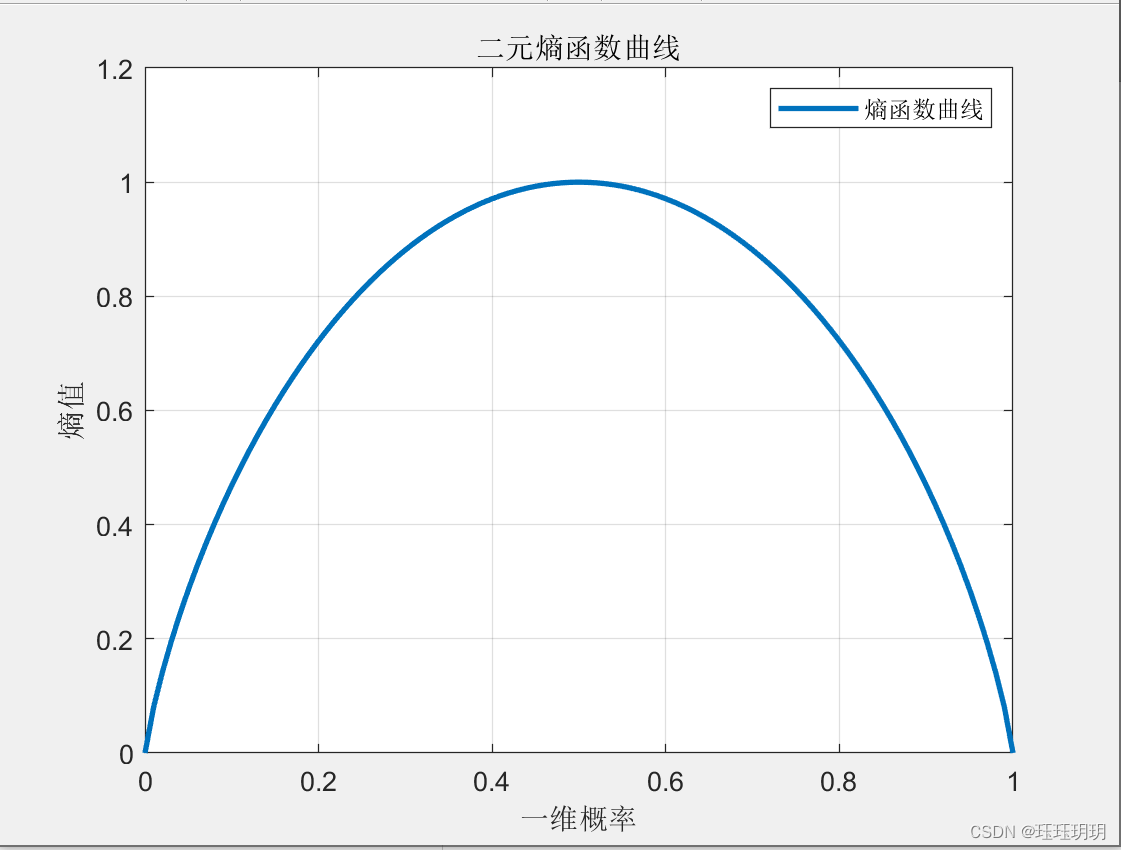
TH:熵函数就是随机分布P的上凸函数。
分析:
对信源无失真编码时,我们无法改变信源符号的原始分布(一个客观事实),但是我们可以对字母表进行一一映射,试图改变编码后符号的概率分布,使得编码后的码字尽可能携带多的信息量,在总信息量不变的前提,就有可能保证平均码长小。一一映射也使得信源的解码无差错。怎么做一一映射属于优化问题,也就是使得编码后的分布成最优分布。由于凸函数的极值就是最值,求极值的方法较为简单。
2:信源的分类

按照:信源符号的取值,以及取值时间的离散或连续两方面去分类。
几种信源信源




3:自信息
1:自信息定义

自信息的意义:在发生前表征事件不确定性的大小,在发生后表征事件所提供的信息量。
2:其他形式自信息

四:离散无记忆扩展信源

五:马尔科夫信源
1:马尔科夫链

马克科夫链的状态转移概率:

:当前时刻为m,从状态i经过n步步长到达状态j的:n步转移概率。
2:齐次马尔科夫链
特点:转移概率与初始时刻无关,也就是转移概率是平稳的


齐次马氏链关键:初始分布+状态概率矩阵。
各态历经性

从w的下标j可知:无论之前处于哪个状态只要步长足够大,最后达到J状态概率相同。
稳态求解:

六:马尔可夫信源的信源熵

时齐马尔科夫信源
条件概率:与时间起点无关,则信源的输出可以看作时齐的马尔可夫链,称此信源为:时齐马尔可夫信源。
例子:注意状态转移矩阵和符号转移矩阵的区别。
求解方法

注意:求熵针对符号,用的是符号条件熵。
计算例子
注意:看输出,这里只输出一个符号,所以符号和状态矩阵等价。
例子2:
注意:输出是两个符号,每个状态是两个符号











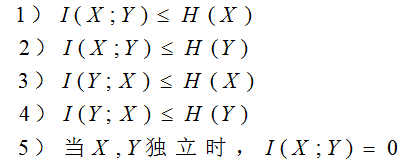
![[信息论与编码] 03. 离散信源、信源熵、联合熵、条件熵](https://img-blog.csdnimg.cn/20190605200610931.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxNzg1Mjg4,size_16,color_FFFFFF,t_70)