本次实验是基础的计算信源熵，代码很简单。

为了便于计算，将概率和不为1的重新输入以及把概率为0删除！！！

format short;                               %定义输出的格式
p = input('p = ');                          %输入任意的信源概率分布
if sum(p) ~= 1                              %判断输入的信源概率之和是否为1error('p is error,sum is not 1')
endzerop = find(p == 0);                       %找到信源中概率为0的符号
if ~isempty(zerop)                          %如果有概率为0的符号，将这个符号删除p(zerop) = [];
end
H = -sum(p.*log2(p));                        %对信源进行信源熵计算
fprintf('entropy is: %d (bit/symbol)',H)    %输出信源熵

 实验结果：

接下来就是二元信源熵的曲线

在这个实验中，由于第一个点和最后一个点为0,需要单独拎出来，其余的熵的公式计算就行。

clear;                               %清空
format short;                        %定义输出格式
L = 0.01;                            %定义间隔
p = L:L:1-L;                         %定义x轴长度
H1 = -p.*log2(p)-(1-p).*log2(1-p);   %计算熵值
n = length(p);                       %计算x轴长度
for i = 1:n+2                        %将0.01到0.99值赋给新的熵值，再加上0和1处的值H(1) = 0;H(2:n+1) = H1(1:99);H(n+2) = 0;
end
p1 = 0:L:1;                         %重新给x轴长度，对应新的熵的长度
plot(p1,H,'LineWidth',2);           %绘图
title('二元熵函数曲线');             %标题
xlabel('一维概率');                 %x轴
ylabel('熵值');                     %y轴
legend('熵函数曲线');               %图例
grid on;                            %上网格
axis([0,1,0,1.2]);                  %规定输出的范围

实验结果：

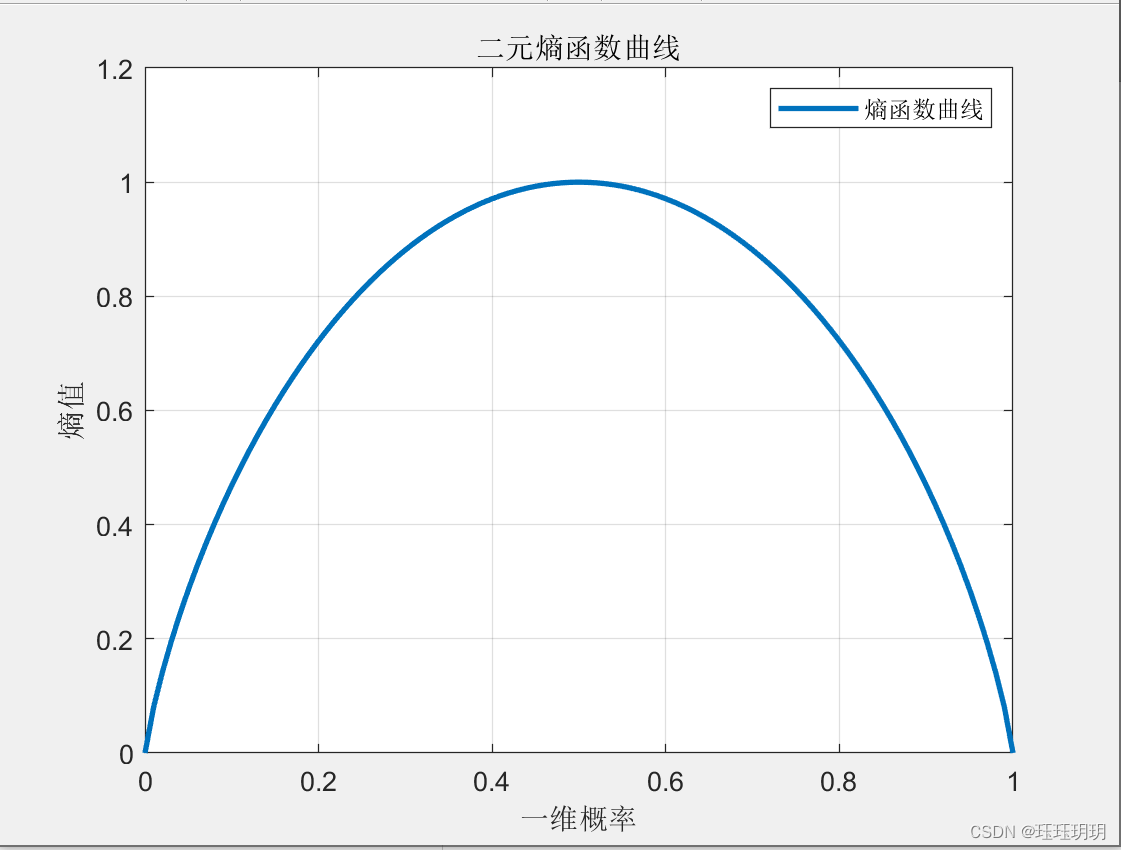
以上就是本次实验的内容。