消息的传递

我们的郭嘉大大在曹操这过得逍遥自在，但是有一天曹操给了他一个任务，在建邺城内有 N 个袁绍的奸细，将他们从 1 到 N 进行编号，同时他们之间存在一种传递关系，即若C{i,j}=1，则奸细 i 能将消息直接传递给奸细 j。

现在曹操要发布一个假消息，需要传达给所有奸细，而我们的郭嘉大大则需要传递给尽量少的奸细使所有的奸细都知道这一个消息，问我们至少要传给几个奸细？

---

我觉得自己写这道题莫名的心态爆炸，第一眼是个并查集，后来发现并不能保证互相传达，因为是有向图

然后想到了Tarjan强联通分量，然后就是一通瞎写

但是我忽略了一个问题，那就是不一定要每个点都要互相到达

例如下图：

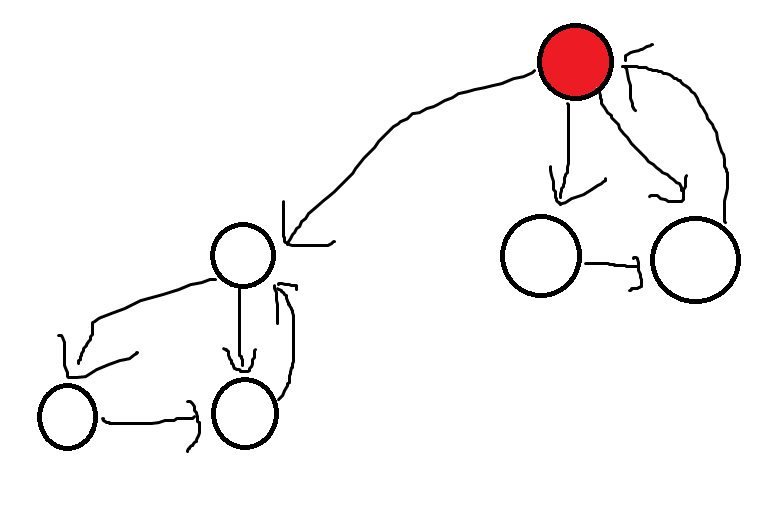
我们可以告诉标红的点，然后所有人就都知道了

所以经过思索，我们可以吧刚才的两个思路结合在一起，也就是先用Tarjan缩点，然后再判断是是否连通

不会缩点的点这里：https://www.cnblogs.com/WWHHTT/p/9825766.html

下面给出代码：

#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
inline int min(int a,int b){return a<b?a:b;}
inline int max(int a,int b){return a>b?a:b;}
inline int rd(){int x=0,f=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';return x*f;
}
inline void write(int x){if(x<0) putchar('-'),x=-x;if(x>9) write(x/10);putchar(x%10+'0');return ;
}
int n,m;
int head1[1000006],nxt1[2000006],to1[2000006];
int total1=0;
void add1(int x,int y){total1++;to1[total1]=y;nxt1[total1]=head1[x];head1[x]=total1;return ;
}
int dfn[100006],low[100006];
int color[100006];
int tot=0;
int color_cnt=0;
int book[100006];
int sta[100006];
int size=0;
void Tarjan(int x,int fa){//TarjanÄ£°å low[x]=dfn[x]=++tot;sta[++size]=x;book[x]=1;for(int e=head1[x];e;e=nxt1[e]){if(!dfn[to1[e]]){Tarjan(to1[e],x);low[x]=min(low[x],low[to1[e]]);}else if(book[to1[e]]) low[x]=min(low[x],dfn[to1[e]]);}if(dfn[x]==low[x]){color[x]=++color_cnt;book[x]=0;while(sta[size]!=x){color[sta[size]]=color_cnt;book[sta[size]]=0;size--;}size--;}return ;
}
int head2[1000006],nxt2[2000006],to2[2000006];
int total2=0;
void add2(int x,int y){total2++;to2[total2]=y;nxt2[total2]=head2[x];head2[x]=total2;return ;
}
int du[1000006];
void change(){for(int i=1;i<=n;i++){for(int e=head1[i];e;e=nxt1[e]){if(color[i]!=color[to1[e]]){add2(color[i],color[to1[e]]);du[color[to1[e]]]++;}}}return ;
}
int main(){n=rd();for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){int x=rd();if(x) add1(i,j);}for(int i=1;i<=n;i++) if(!dfn[i]) Tarjan(i,0);change();int ans=0;for(int i=1;i<=color_cnt;i++) if(!du[i]) ans++;write(ans);return 0;
}