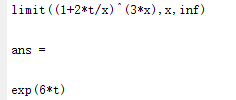符号运算主要是结合高等数学和微积分的知识
常用的符号运算有极限、微分、积分等

极限

“极限”是数学中的分支——微积分的基础概念，广义的“极限”是指“无限靠近而永远不能到达”的意思。数学中的“极限”指：某一个函数中的某一个变量，此变量在变大（或者变小）的永远变化的过程中，逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”（“永远不能够等于A，但是取等于A‘已经足够取得高精度计算结果）的过程中，此变量的变化，被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近A点的趋势”。极限是一种“变化状态”的描述。此变量永远趋近的值A叫做“极限值”

在MATLAB中计算极限

函数：limit
调用格式：

syms ;                   %定义变量，有几个变量就定义几个
g=limit (f);             %f为所求式子的极限,默认趋向于0
g=limit (f,a);           %f为所求式子趋于a的极限
g=limit (f,x,a);         %f为所求极限的式子,x为对x求极限(因为有些式子会有多个变量，比如x、t、h等),a为趋向于a
g=limit (f,x,a,'left');  %f为式子,x为对x求,a为趋向于a，left为求左极限
g=limit (f,x,a,'right'); %f为式子,x为对x求,a为趋向于a,right为求右极限

例：求以下的极限：

syms x;
limit(sin(x)/x)
syms x;
limit((x-2)/(x^2-4),2)
syms x t;
limit((1+2*t/x)^(3*x),x,inf)
syms x h;
limit((sin(x+h)-sin(x))/h,h,0);

如下：