目录
一、极限命令
1.双侧极限
2.单侧极限
二、绘制极限图像
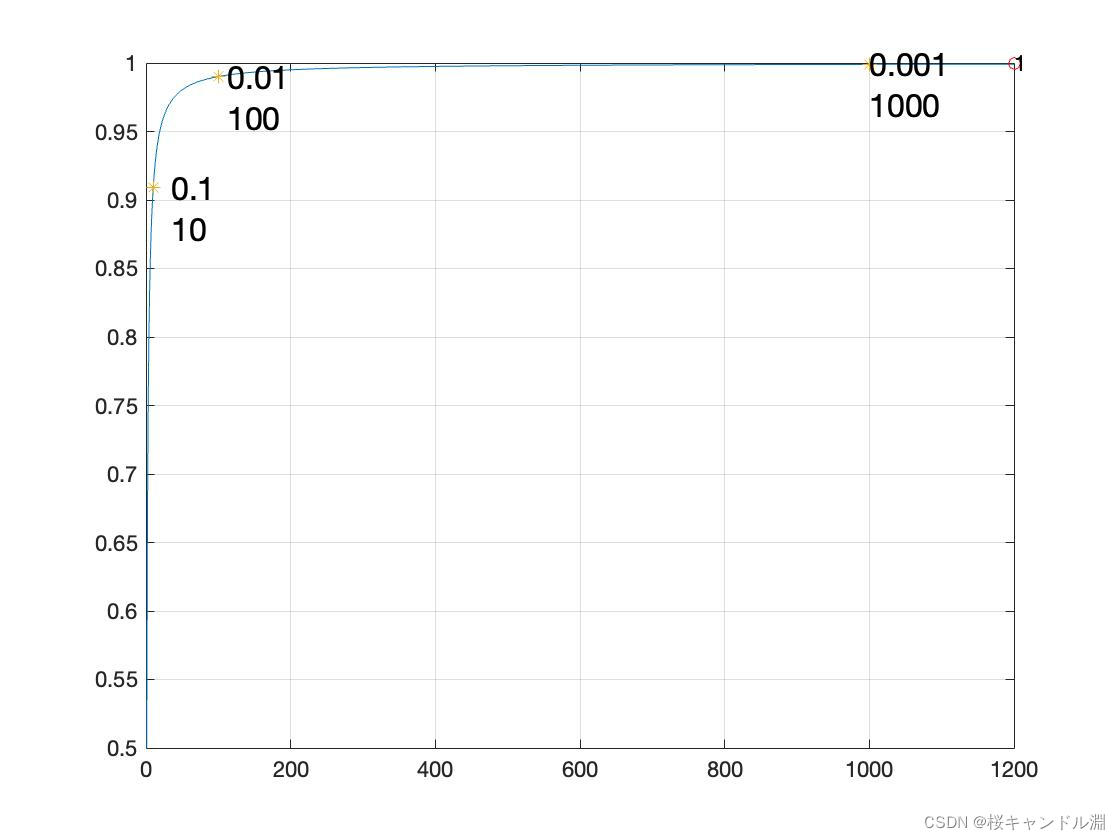
1.绘制f(x)=n/(n+1)图像
2.绘制编辑
3.绘制编辑
三、绘制递推数列的图像
四、使用元胞来求函数极限
五、绘制多个族的图像
一、极限命令
数列极限命令 limit(F,n,inf)
F是表达式,n是离散变量,inf是无穷大)
syms n
limit((3*n+1)/(2*n+1),n,inf)
1.双侧极限
syms xlimit((x^3-1)/(x^2-5*x+3),x,2)

2.单侧极限
函数单侧极限命令 limit(F,x,a,’left’) limit(F,x,a,’right’)
syms x
limit(1/x,x,0,'left')
二、绘制极限图像
1.绘制f(x)=n/(n+1)图像
clear
clc
syms n
an=n/(n+1);
l=limit(an,n,inf);
%将符号极限转变为数值
l=double(l);
%将我们符号转变为具体的函数
fn=inline(an);
%假定一个无穷大的取值
nm=1200;
n=1:nm;
figure
%绘制fn(n)的图像
plot(n,fn(n))
grid on
hold on
%在我们接近无穷大的地方用红色画一个全
plot(nm,1,'or')
%标注文本1
text(nm,1,num2str(1))
n=3;
%取三个无穷小的位置
epsilon=1./10.^(1:n);
%向下取整
nc=floor(1./epsilon);
plot(nc,fn(nc),'*')
text(nc,fn(nc),num2str(epsilon'),'FontSize',16)
text(nc,fn(nc)-0.03,num2str(nc'),'FontSize',16)
2.绘制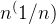
clear
clc
syms n
an=n.^(1/n);
fn=inline(an);
nm=1200;
n=1:nm;
figure
plot(n,fn(n))
grid on
hold on
plot(nm,1,'or')
text(nm,1,num2str(1))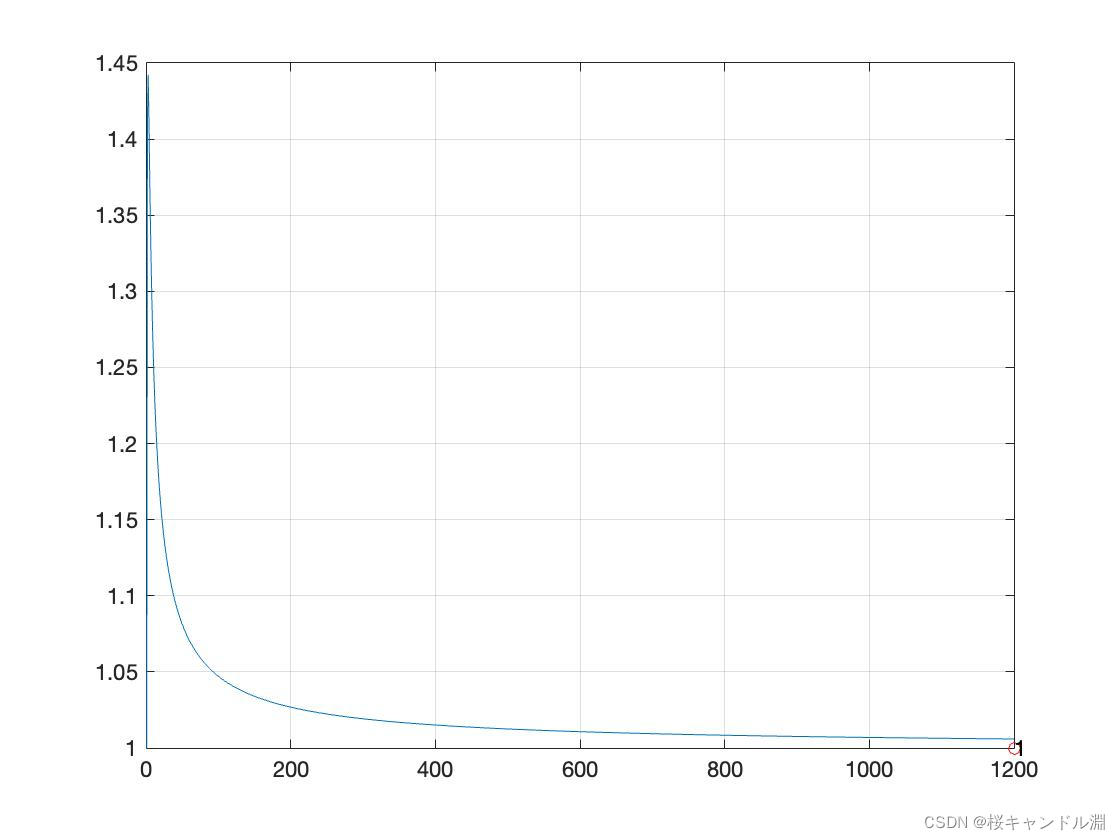
3.绘制
clear
clc
syms n
an=3*n.^2+n/(2*n^2-1);
fn=inline(an);
nm=1200;
n=1:nm;
figure
plot(n,fn(n))
grid on
hold on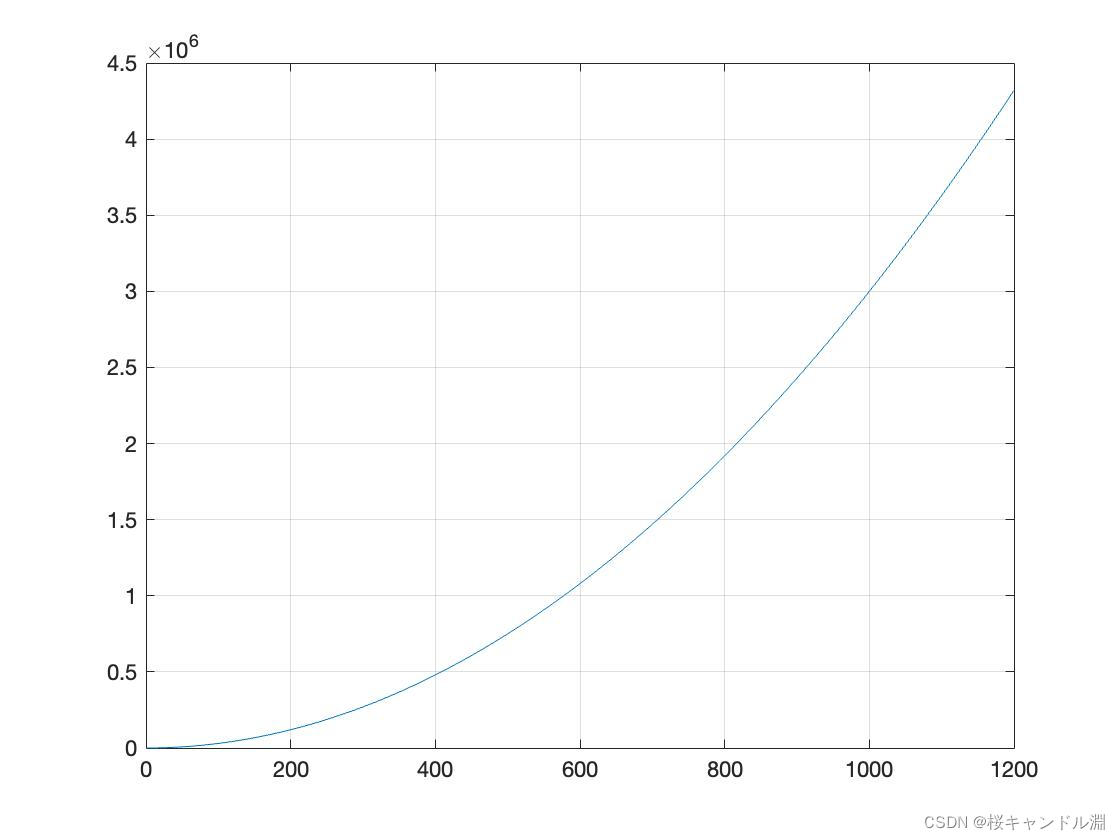
在观察上面的命令中,我们发现绘图的方法非常相似,所以我们可以写一个函数来方便地绘制图像
clear %清除变量
syms n %定义符号变量
an=(3*n^2+n)/(2*n^2-1); %数列的符号通项
nm=50; %最大整数
tit='二次整数分式'; %标题的一部分
fun(an,nm,tit) %调用函数文件求极限
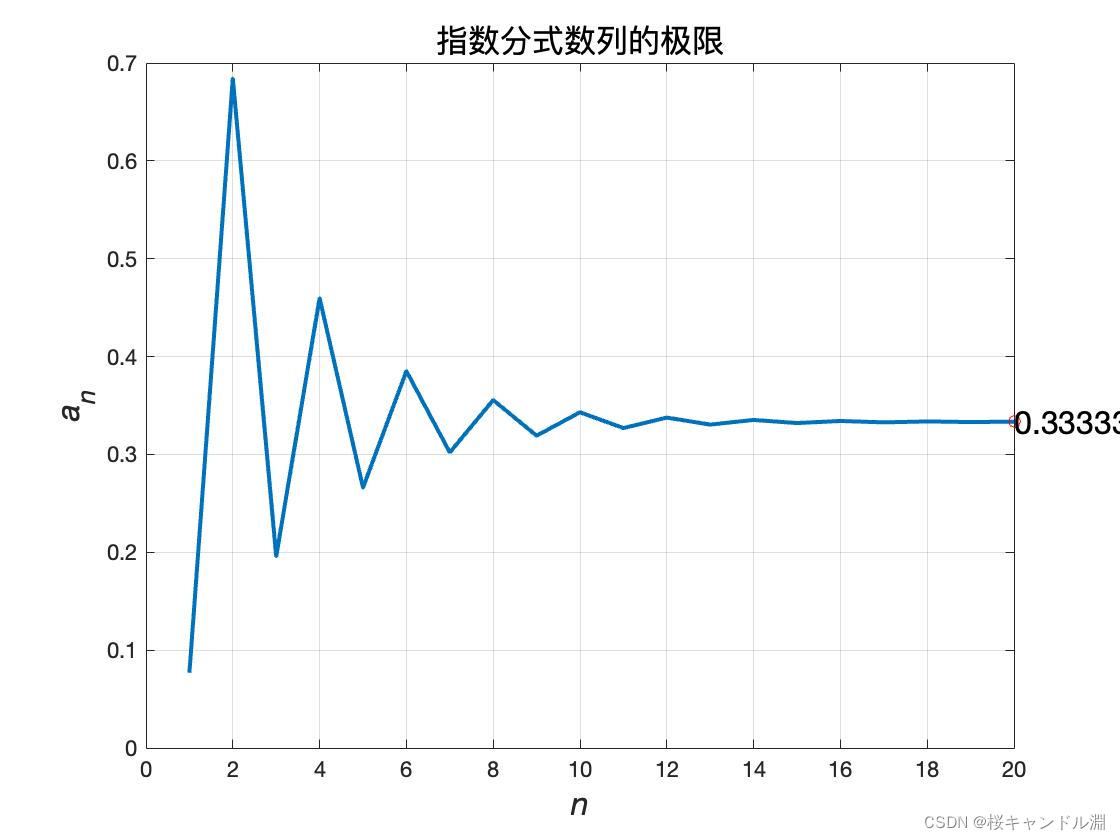
fun(((-2)^n+3^n)/((-2)^(n+1)+3^(n+1)),20,'指数分式')%调用函数文件求极限
fun(sqrt(n^2+n)-n,200,'根式差') %调用函数文件求极限
fun((1-1/2^(1/n))*cos(n),100,'高次根式复合')%调用函数文件求极限%定义一个函数来绘制图像,第一个参数为数列的公式,第二个为极限范围,第三个为标题
function fun(an,nm,tit)
syms n %定义符号变量
l=limit(an,n,inf); %求符号极限
l=double(l); %化为数值
fn=inline(an); %符号数列化为内线函数
n=1:nm; %整数向量
figure %创建图形窗口
plot(n,fn(n),'LineWidth',2) %画数列曲线
xlabel('\itn','FontSize',16) %加横坐标
ylabel('\ita_n','FontSize',16) %加纵坐标
title([tit,'数列的极限'],'FontSize',16)%加标题
grid on %加网格
hold on %保持图像
plot(nm,l,'or') %在有限远处画极限值
text(nm,l,num2str(l),'FontSize',16) %标记极限
end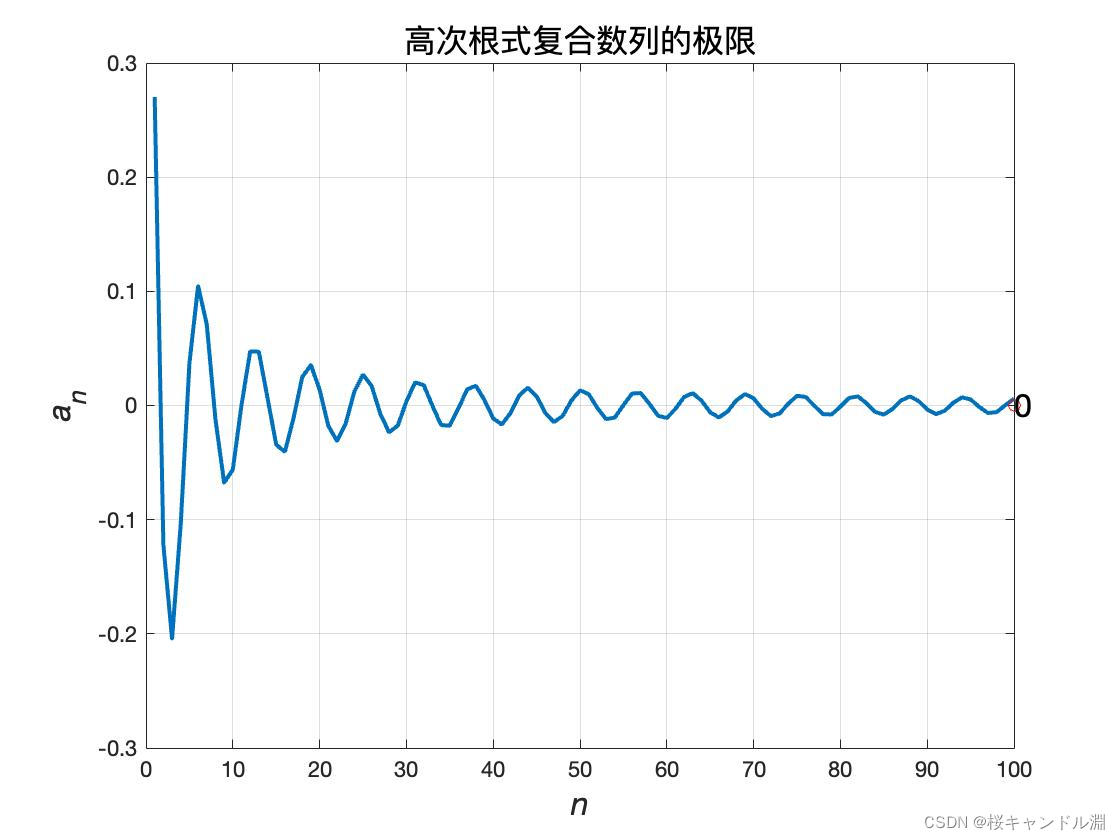


三、绘制递推数列的图像
绘制的图像
clear
a0=1;
an=a0;
nm=10;
%将我们的数据迭代地拼接到原来的数据后面
for n=1:nma0=1+a0./(1+a0);an=[an;a0];
end
n=0:nm;
figure
plot(n,an,'*-')
四、使用元胞来求函数极限
%多个有理函数的极限
clear %清除变量
syms x %定义符号变量
%这里我们创建了一个元胞来将不同的函数传入
fc={(x^3-2*x-1)/(x^5-2*x-1),((1+x)*(1+2*x)*(1+3*x)-1)/x,...(x^3-3*x+2)/(x^4-4*x+3),...(x-1)*(x-2)*(x-3)*(x-4)*(x-5)/(5*x-1)^5};%符号函数元胞
n=length(fc); %元胞个数
for i=1:n %按元胞循环f=fc{i} %取函数if i<n %如果小于总数l=limit(f,x,i-2); %求符号极限else %否则l=limit(f,x,inf); %求符号极限end %结束条件l=double(l) %化为数值
% pause
end %结束循环
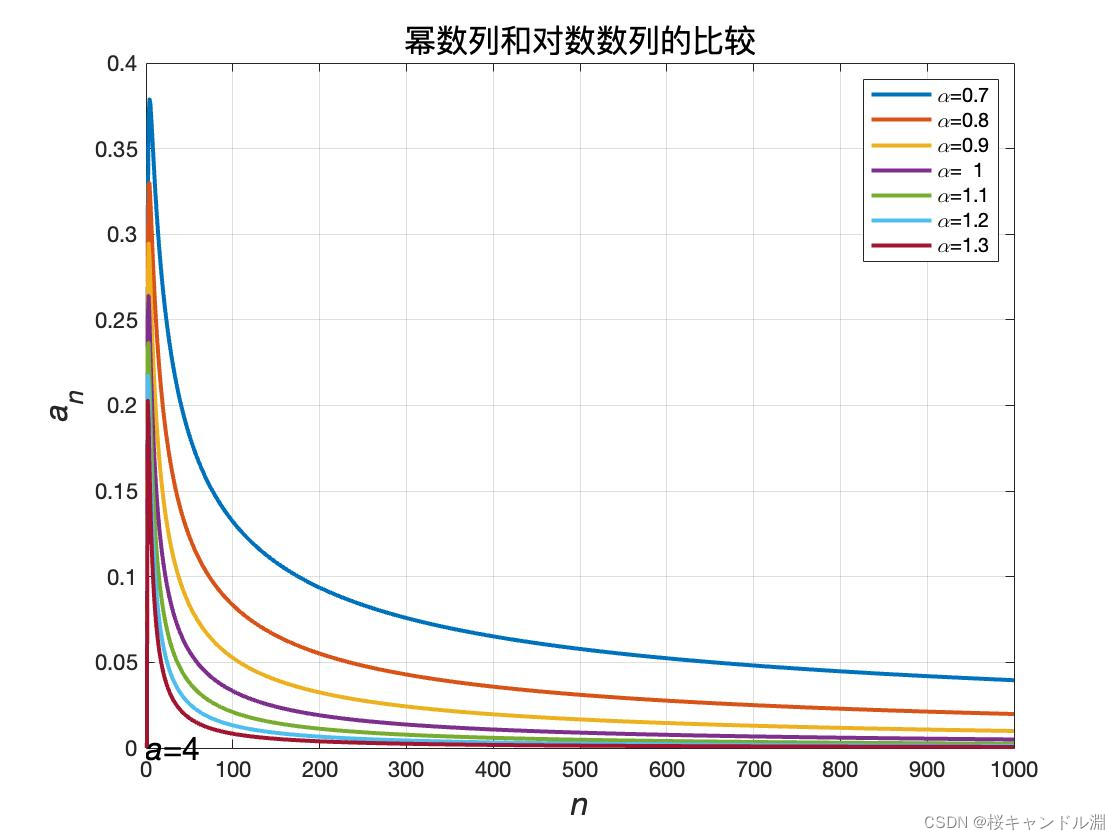
五、绘制多个族的图像
绘制多个族的图像我们需要用到meshgrid来帮助我们同时绘制多个线条。
%幂数列和对数数列的比较
clear %清除变量
a=input('请输入底数a(>1):'); %键盘输入底数
alpha=0.7:0.1:1.3; %指数向量
n=1:1000; %整数向量
[N,A]=meshgrid(n,alpha); %整数和指数矩阵
Yn=log(N)/log(a)./N.^A; %通项
figure %创建图形窗口
plot(n,Yn,'LineWidth',2) %画曲线族
title('幂数列和对数数列的比较','FontSize',16)%加标题
xlabel('\itn','FontSize',16) %加横坐标
ylabel('\ita_n','FontSize',16) %加纵坐标
grid on %加网格
legend([repmat('\it\alpha\rm=',length(alpha),1),num2str(alpha')])%加图例
text(0,0,['\ita\rm=',num2str(a)],'FontSize',16)%加说明