基于MATLAB的极限与求导（附完整代码）

article/2025/4/29 6:39:26

一. 极限问题的解析解

1.1 单变量函数的极限

$L=\lim_{x\to x_0}f(x)$

MATLAB格式：

L=limit(fun,x,x_0)

我们知道数学中极限有两种形式：

$L_1=\lim_{x\to x^-_0}f(x),\quad L_2=\lim_{x\to x^+_0}f(x)$

所以，MATLAB中格式为：

L=limit(fun,x,x0,'left')L=limit(fun,x,x0,'right')

例题1

求解极限问题：

$\lim_{x\to \infty}x(1+\frac{a}{x})^xsin\frac{b}{x}$

解：

代码：

clc;clear;
syms x a b;
f=x*(1+a/x)^x*sin(b/x);
L=limit(f,x,inf)

运行结果：

L =b*exp(a)

例题2

求解单边极限问题：

$\lim_{x\to 0^+}\frac{e^{x^3}-1}{1-cos\sqrt{x-sinx}}$

解：

代码如下：

clc;clear;
syms x;
limit((exp(x^3)-1)/(1-cos(sqrt(x-sin(x)))),x,0,'right')%在(-0.1,0.1)区间绘制出函数曲线
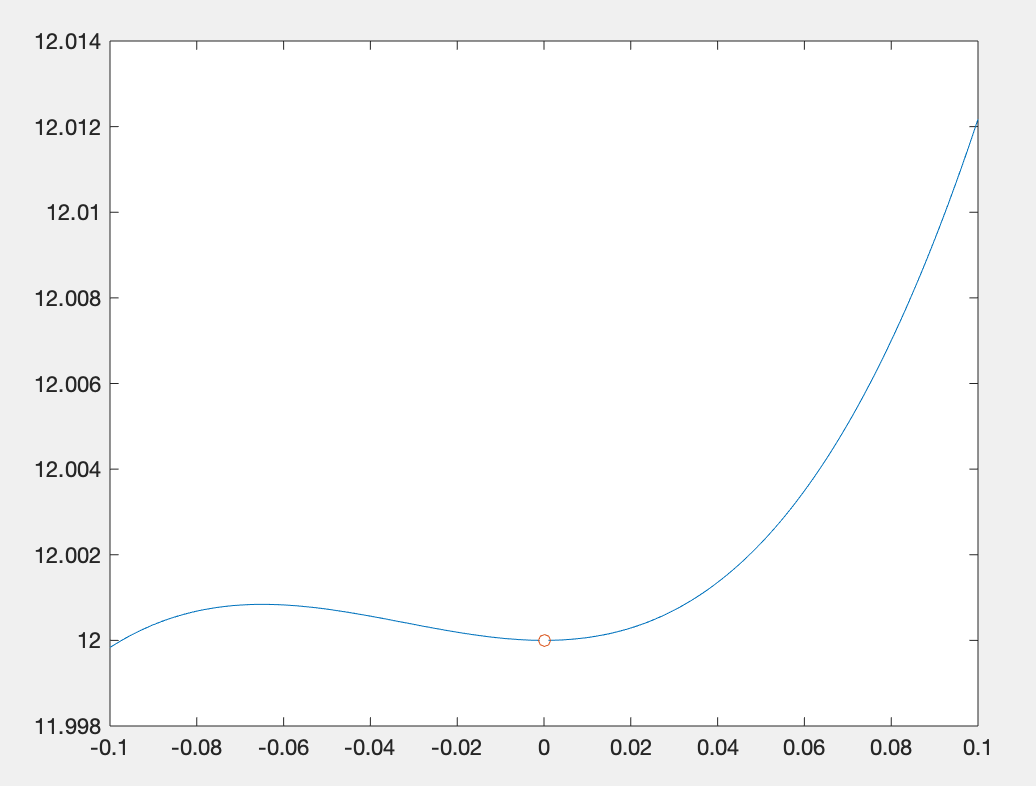
x=-0.1:0.001:0.1;
y=(exp(x.^3)-1)./(1-cos(sqrt(x-sin(x))));
plot(x,y,'-',[0],[12],'o')

运行结果：
ans =12

1.2 多变量函数的极限

$L=\lim_{x\to x_0,y\to y_0}f(x,y)$

MATLAB格式：

%格式1
L1=limit(limit(f,x,x0),y,y0)%格式2
L2=limit(limit(f,y,y0),x,x0)

如果x0或y0不是确定的值，而是另一个变量的函数，如x=g(y)，则上述的极限求取顺序不能随意改变。

例题3

求出二元函数极限值

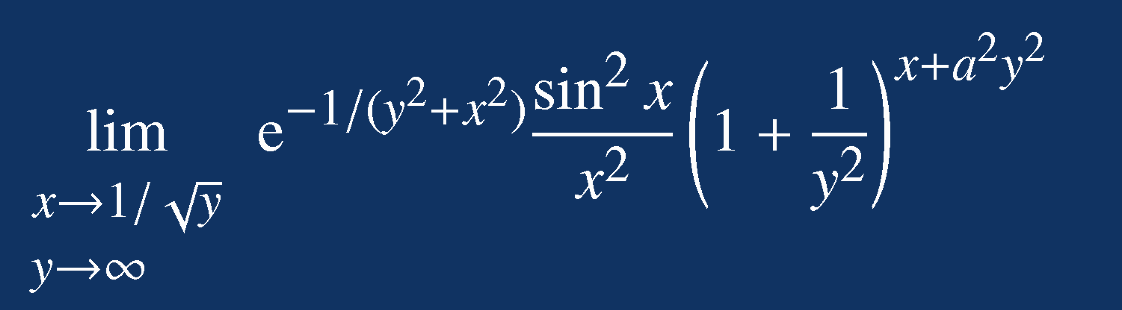
解：

MATLAB代码：

clc;clear;
syms x y a;
f=exp(-1/(y^2+x^2))*sin(x)^2/x^2*(1+1/y^2)^(x+a^2*y^2);
L=limit(limit(f,x,1/sqrt(y)),y,inf)

运行结果：

L =limit(y^(1 - 2*a^2*y^2 - 2/y^(1/2))*sin(1/y^(1/2))^2*exp(-y/(y^3 + 1))*(y^2 + 1)^(1/y^(1/2) + a^2*y^2), y, Inf)

二. 导数的解析解

2.1 单变量函数

函数的导数与高阶导数：

$\frac{df(x)}{dx}\quad \frac{d^nf(x)}{dx^n}$

MATLAB格式：

y=diff(fun,x) %求导数
y=diff(fun,x,n)  %求n阶导数

例题4

函数f(x):

$f(x)=\frac{sinx}{x^2+4x+3}$

求该函数的各阶导数。

解：

MATLAB代码：

clc;clear;
syms x;
f=sin(x)/(x^2+4*x+3);%一阶导数
f1=diff(f);
pretty(f1)%原函数及一阶导数图
x1=0:.01:5;
y=subs(f,x,x1);
y1=subs(f1,x,x1);
plot(x1,y,x1,y1,':')%原函数的4阶导数
f4=diff(f,x,4);
pretty(f4)%更高阶导数
tic,diff(f,x,100);toc %运算会比较慢

运行结果：

2.2 多元函数的偏导

已知二元函数f(x,y)，则偏导数学形式如下：

$\frac{\partial^{m+n}f}{(\partial x^m\partial y^n)}$

MATLAB格式：

%格式1
f=diff(diff(f,x,m),y,n)%格式2
f=diff(diff(f,y,n),x,m)

例题5

求此函数的偏导数并用图表示。

$z=f(x,y)=(x^2-2x)e^{-x^2-y^2-xy}$

解：

MATLAB代码：

clc;clear;
syms x y;
z=(x^2-2*x)*exp(-x^2-y^2-x*y);%对x偏导
zx=simplify(diff(z,x))%对y偏导
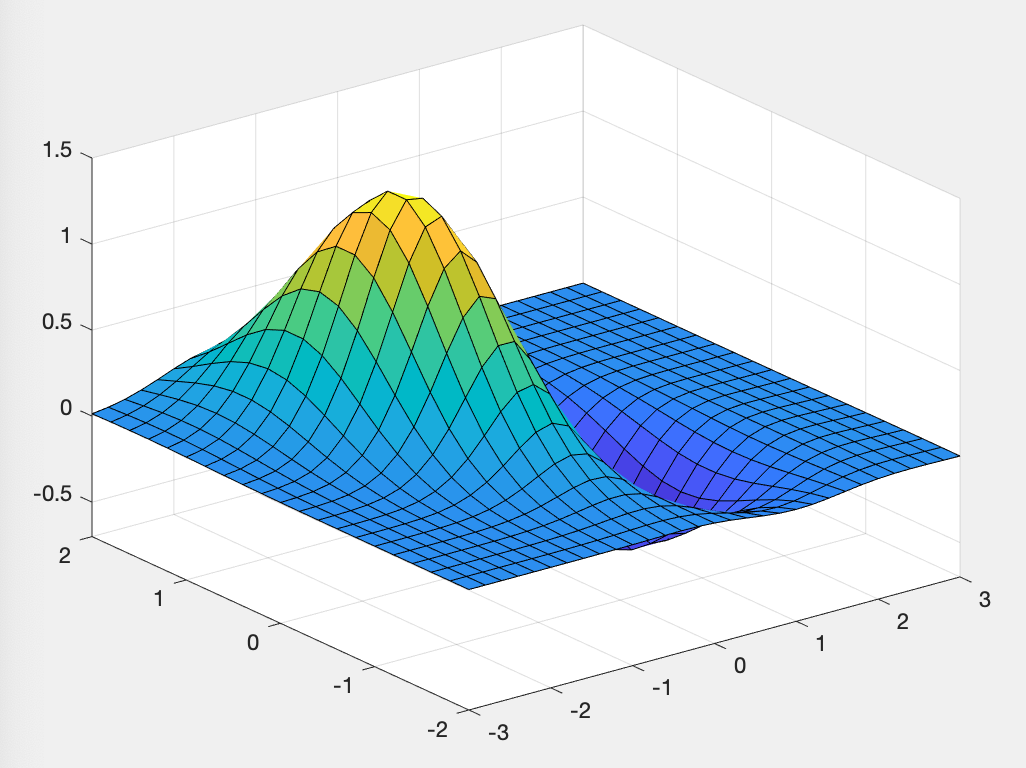
zy=diff(z,y)%直接绘制三维曲面
[x,y]=meshgrid(-3:.2:3,-2:.2:2);
z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
surf(x,y,z),axis([-3 3 -2 2 -0.7 1.5])%绘制等值线
figure,
contour(x,y,z,30),hold on
zx=-exp(-x.^2-y.^2-x.*y).*(-2*x+2+2*x.^3+x.^2.*y-4*x.^2-2*x.*y);
zy=-x.*(x-2).*(2*y+x).*exp(-x.^2-y.^2-x.*y); %偏导的数值解
hold on,
quiver(x,y,zx,zy)

运行结果：

例题6

已知f(x,y,z)：

$f(x,y,z)=sin(x^2y)e^{-x^2y-z^2}$

求解如下偏导：

$\frac{\partial^4f(x,y,z)}{(\partial x^2\partial y\partial z)}$

解：

MATLAB代码：

clc;clear;
syms x y z;
f=sin(x^2*y)*exp(-x^2*y-z^2);
df=diff(diff(diff(f,x,2),y),z);
df=simplify(df);
pretty(df)

运行结果：

三. 多元函数的Jacobi矩阵

给定函数

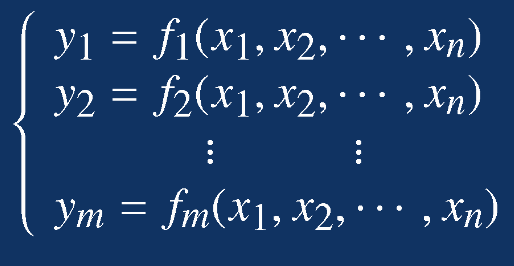
该函数的Jacobi矩阵J如下：

MATLAB格式：

J=jacobian(Y,X)
%X是自变量构成的向量
%Y是由各个函数构成的向量

例题7

推导以下函数的Jacobi矩阵：

$x=rsin\theta cos\phi,y=rsin\theta sin\phi,z=rcos\theta$

解：

MATLAB代码：

clc;clear;
syms r theta phi;
x=r*sin(theta)*cos(phi);
y=r*sin(theta)*sin(phi);
z=r*cos(theta);
J=jacobian([x;y;z],[r theta phi])

运行结果：

J =
[ cos(phi)*sin(theta), r*cos(phi)*cos(theta), -r*sin(phi)*sin(theta)]
[ sin(phi)*sin(theta), r*cos(theta)*sin(phi), r*cos(phi)*sin(theta)]
[ cos(theta), -r*sin(theta), 0]