一、两种处理器的结构体系

1、哈佛结构体系（Harvard architecture）

在这里插入图片描述

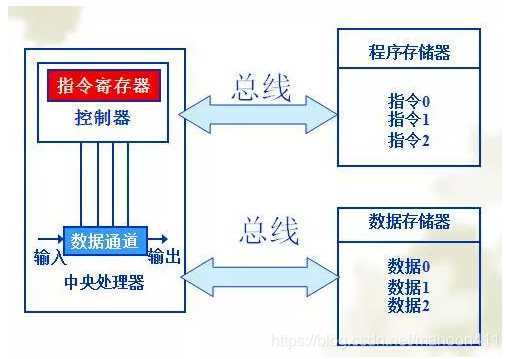
哈佛结构是一种将程序指令存储和数据存储分开的存储器结构。中央处理器首先到程序指令存储器中读取程序指令内容，解码后得到数据地址，再到相应的数据存储器中读取数据，并进行下一步的操作（通常是执行）。程序指令存储和数据存储分开，可以使指令和数据有不同的数据宽度，如Microchip公司的PIC16芯片的程序指令是14位宽度，而数据是8位宽度。

目前使用哈佛结构的中央处理器和微控制器有很多，除了上面提到的Microchip公司的PIC系列芯片，还有：

ATMEL：AVR系列
ARM：ARM9、ARM10和ARM11，Cortex-M3系列，Cortex-M4系列
Interl：51系列内核
Microchip：PIC系列

2、冯·诺依曼结构体系

在这里插入图片描述

冯·诺伊曼结构也称普林斯顿结构，是一种将程序指令存储器和数据存储器合并在一起的存储器结构。程序指令存储地址和数据存储地址指向同一个存储器的不同物理位置，因此程序指令和数据的宽度相同，如英特尔公司的8086中央处理器的程序指令和数据都是16位宽。

目前使用冯·诺伊曼结构的中央处理器和微控制器有很多。除了上面提到的英特尔公司的8086，还有：

Interl：其他中央处理器
ARM：Cortex-A、Cortex-M0和ARM7
MIPS：MIPS处理器
Ti：MSP430系列

3、两种结构的总结

哈佛结构和冯.诺依曼结构都是一种存储器结构。哈佛结构是将指令存储器和数据存储器分开的一种存储器结构；而冯.诺依曼结构将指令存储器和数据存储器合在一起的存储器结构。

哈佛结构的优势

使用冯·诺依曼结构的计算机–程序和数据区域在同一个存储器上它们物理上是连续的，即程序空间不封闭，程序空间的数据在运行时理论上是可以被修改，此外程序一旦跑飞也有可能运行到数据区，虽然都是一些不常见的特殊情况下。

但是哈佛结构的计算机在这些情况下是怎样的呢？基于哈佛结构的处理器入MCS-51，不需要可以对代码段进行写操作的指令，所以不会有代码区被改写的问题；程序只能在封闭的代码区中运行，不可能跑到数据区，这也是跑飞的几率减少并且跑飞后的行为有规律（数据区的数据是不断变化的而代码区是不变的）。所以，相对于冯·诺依曼结构，哈佛结构更加适合于那些程序固化、任务相对简单的控制系统。

哈佛结构采用数据存储器与程序代码存储器分开，各自有自己的数据总线与地址总线。但这是需要CPU提供大量的数据线，因而很少使用哈佛结构作为CPU外部构架来使用。但是对于CPU内部，通过使用不同的数据和指令cache，可以有效的提高指令执行的效率，因而目前大部分计算机体系都是CPU内部的哈弗结构+CPU外部的冯·诺伊曼的结构。

冯·诺依曼结构的优势

待续

当前很多芯片都是混合结构

二、单片机程序的内存分配

统称	具体实际的硬件器件
ROM	Flash、EEPROM、NANDFlash、EMMC、SD卡、TF卡
RAM	SRAM、DRAM、SDRAM、DDR、DDR2、DDR3、DDR4

单片机程序在编译、链接之后会生成hex文件，通过下载工具烧录到芯片内部的ROM里面去，由于单片机的工作特性，所以一般单片机内部ROM都是NOR Flash，NOR Flash具有寻址功能可以在上面运行程序。下图就是通过单片机下载工具烧录到单片机Flash里面去之后的Flash空间区域分布图：

单片机hex文件在Flash上的数据区域分布其中：

Code：为程序代码部分
Ro-data：表示程序定义的常量（const修饰的常量、#define 宏定义等）;
Rw-data：表示已初始化的全局变量
Zi-data：表示未初始化的全局变量（Zi-data可以表示RAM未上电时整个区域的状态，或者上电初始化之后未被使用的区域，上表仅仅描述的是ROM区域的空间分布）

而栈区(stack)、堆区(heap)、全局区（静态区）(static)、文字常量区和程序代码区和上面所介绍的Code、Ro-data等的关系。

1、栈区（stack）：由编译器自动分配释放，存放函数的参数值，局部变量的值等。其操作方式类似于数据结构中的栈。这些值是可读写的，那么stack应该被包含在RW-data(读写数据存储区)，也就是单片机的sram中。
2、堆区（heap）：一般由程序员分配释放，若程序员不释放，程序结束时可能由OS回收。可以理解，这些也是被包含在单片机的sram中的。
3、全局区（静态区）（static）：全局变量和静态变量的存储是放在一块的，初始化的全局变量和静态变量在一块区域，未初始化的全局变量和未初始化的静态变量在相邻的另一块区域，程序结束后由系统释放。这些数据也是可读可写的，和stack、heap一样，被包含在RAM中。
4、文字常量区：常量字符串就是放在这里的。这些数据是只读的，分配在Ro-data(只读数据存储区)，则被包含在flash中。
5、程序代码区：存放函数体的二进制代码，可以想象也是被包含在flash，因为对于MCU来说，当其重新上电，代码还会继续运行，并不会消失，所以存储在flash中。

下图是初始化之前的ROM和RAM中的数据分布：

1、未初始化之前的RAM里面所有区域都是随机的值即：Zi-data

下图是初始化之后的ROM和RAM中的数据分布：

1、初始化的时候会由Boot程序（进入main函数之前）拷贝Flash里面的Rw-data区域到RAM

下图是初始化之后正常运行时，单片机内ROM和RAM区域分布图：

上电初始化之后Flash的Rw-data就不会再使用了，除非重新上电、复位了boot才会重新从ROM（Flash）中拷贝Rw-data区域到RAM中去。
运行时，根据上一节对哈佛模型的描述（51内核、Cortex-M3、Cortex-M4是哈佛模型）,程序存储区对应ROM（Flash）数据存储区对应RAM，如此这般两个区域就是物理上的分开的–经典的哈佛模型。

在这里插入图片描述

三、单片机程序和操作系统应用程序的对比

操作系统应用程序	描述	对应单片机程序
BSS段–.bss	未初始化的全局变量、静态变量，一旦初始化就回收，并转存到数据段之中	Zi-data
代码段–.code	代码，程序结束的时候系统会自动回收存储在代码段中的数据，内存区域较小	Code
数据段–.data	已经初始化的全局变量、静态变量，直到程序结束的时候才会被回收	Rw-data (global/static)
堆–.heap	动态分配内存，alloc出来的对象，需要程序员进行内存管理	Rw-data (heap)
栈–.stack	局部变量，自动分配内存，当局部变量的作用域执行完毕之后就会被系统立即回收	Rw-data (stack)