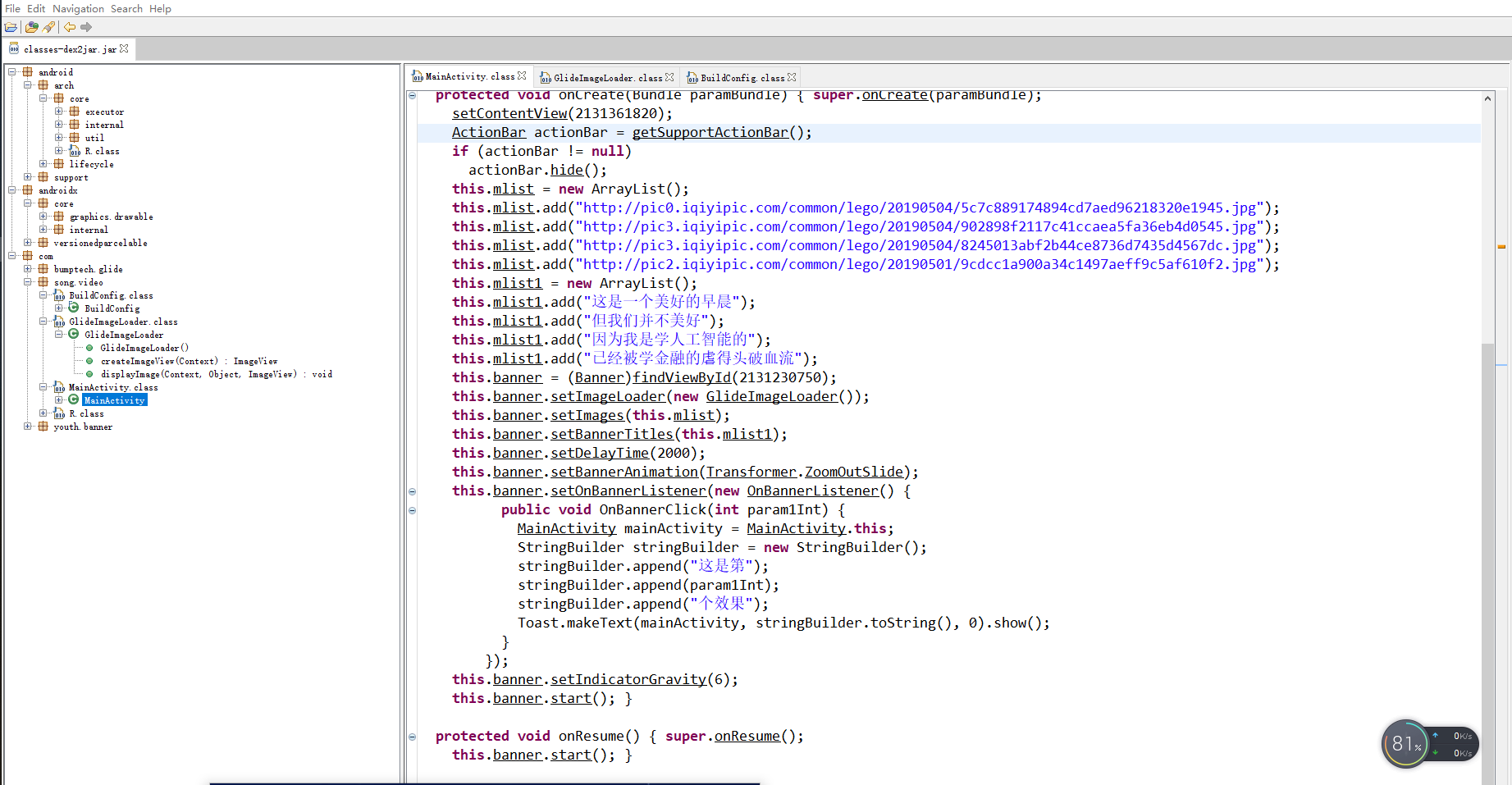
你好,我是 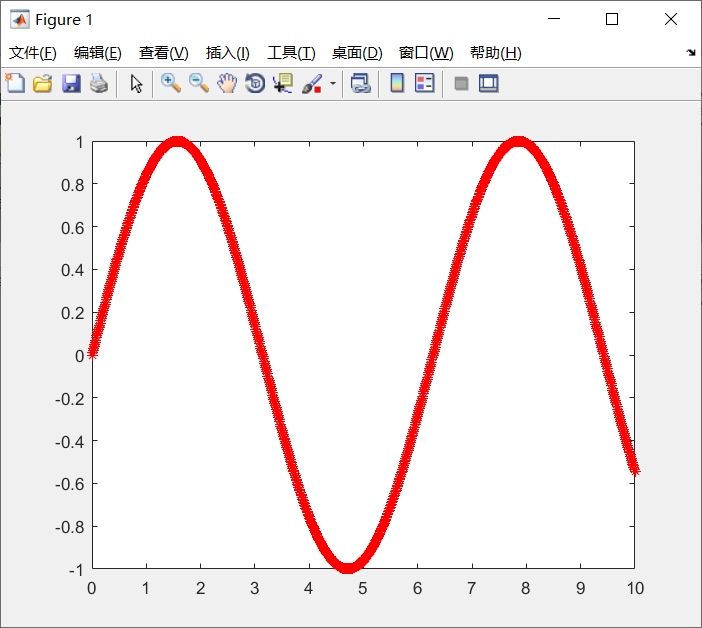 可以看到,x是一个长度为1001的一维数组,y是和x等长的在sin(x)上的一维数组,后边的
可以看到,x是一个长度为1001的一维数组,y是和x等长的在sin(x)上的一维数组,后边的
这些就是基本的绘图参数指令,搭配使用效果更佳。 关于参数的使用是在每种方法中都可以添加,三种常用示例只是简单示例。关于第三种使用方法,意思是把n个图像做出在一个窗口中,同时也少敲了几个plot,当然,如果你想把代码分开写也可以,只需要加上 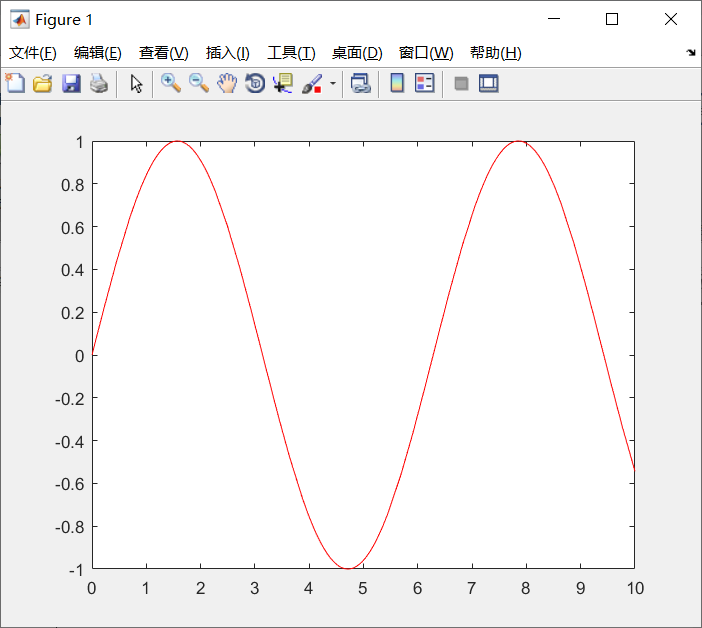
在第二种方法中,funx、funy代表函数,通常采用函数句柄的形式。tlims为参数函数funx和funy的自变量的取值范围,用二元向量[tmin,tmax]描述。如绘制参数方程(x=t sint,y=tcost)曲线如下:
goldsunC让我们一起进步吧! 使用Matlab绘图
图像是结果的一种可视化表现,它能直观的体现你的结果,并且能体现你获得结果的准确性,在当前的大数据时代,在做数据分析的时候,将其可视化可以直观多维的展示数据,可以让人们更好的发现并且记住数据的特征,因此很多时候掌握一些绘图方法是非常重要的,而使用MATLAB可以非常简单的进行绘图(当然还有很多其它工具可供使用),下文是我所了解的一些基本绘图方法的整理,其中很多很多内容非常基础,希望对你能有些帮助。二维作图
二维图像是我们在学习过程中经常会接触到的图像,比如在做数学题目时随手画出的一个正弦曲线,这个图像往往是我们根据它的函数做出来的,事实确是这样,在我们学习过程中画出来的每一个图像几乎都是函数,反过来说,每一个函数都对应着它自己的图像,我们能画出来的二维图像往往是一个一元函数即二元方程,在Matlab中做二维图像也是这样,我们根据一个函数来画出它的图像,不过要注意的一点是, 在Matlab画图的过程中,它并不认识你给出的那个函数,它要做的仅仅是把你给出的函数上的点连成线而已。- plot和fplot
plot()和 fplot()函数,其中,plot的经常使用的方法有下面三种: one plot(x)
two plot(x,y,参数)
three plot(x1,y1,x2,y2,...,xn,yn)
y = [5,10,15,20]
z = [100,200,300,400]
x =y+z*i
//这里的x经过此定义将会被认为是一个复数变量
//图像将会以实部即y为横坐标,虚部即z为纵坐标作图
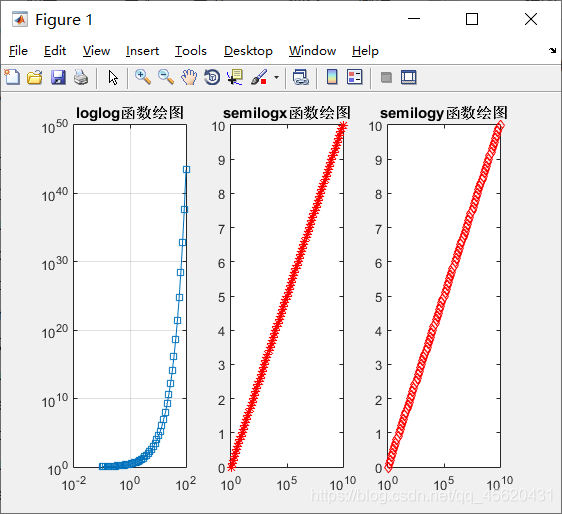
x = [0:0.01:10]
y = sin(x)
plot(x,y,'-r*')
 可以看到,x是一个长度为1001的一维数组,y是和x等长的在sin(x)上的一维数组,后边的
可以看到,x是一个长度为1001的一维数组,y是和x等长的在sin(x)上的一维数组,后边的 -r*分别为曲线线性、颜色、数据点标记,其中参数的一些具体属性如下表所示: | 线形 | 颜色 | 数据点标记 |
|---|---|---|
'-' : 实线 | 'k' : 黑色 | * : 星号 |
':' : 虚线 | b : 蓝色 | o : 圆圈 |
'-.' : 点划线 | c : 蓝绿色 | s : 方块 |
'--' : 双划线 | g : 绿色 | p : 五角星 |
m : 洋红色 | ^ : 朝上三角符号 | |
r : 红色 | X : 叉 | |
w : 白色 | + : + | |
y : 黄色 | d : 菱形 | |
v : 朝下三角符号 | ||
< : 朝左三角符号 | ||
> : 朝右三角符号 | ||
H : 六角形 |
hold on命令就行了,关于它后文会有介绍。而关于fplot,其基本使用方法如下: one fplot(f,lims,参数)
two fplot(funx,funy,tlims,参数)
fplot(@(x)sin(x),[0,10],'-r')

fplot(@(t)t.*sin(t),@(t)t.*cos(t),[0,10*pi],'-r')