MATLAB画图——基础篇
在MATLAB使用的过程中,学会画图是一项必要的技能。在这里,我总结了部分简单的画图函数,同时附上代码(本文中的程序为了方便给出的数据都很简单,大家可以自己去尝试其他数据)。这对刚刚开始接触MATLAB的小白来说,我认为还是很有帮助的。
文章目录
- 一、plot()函数
- 1.二维图形
- (1)绘图选项
- (2)图形的辅助标注和窗口的分割
- (3)格式
- 2.三维图形
- (1)格式
- (2)网格矩阵生成函数:meshgrid
- (3)mesh函数
- (4)surf函数
- 二、特殊图形
- 1.对数坐标图
- 2.极坐标图
- 3.条形图
- 4.面积图
- 5.饼状图
- 6.双y轴
- 7.罗盘图
- 8.羽毛图
- 9.矢量图
- 10.散点图
- 总结
- 参考
一、plot()函数
1.二维图形
(1)绘图选项
| 线型 | 颜色 | 标记符号 | |
|---|---|---|---|
| -实线 | b蓝色 | .点 | s方块 |
| :虚线 | g绿色 | o圆圈 | d菱形 |
| .-点划线 | r红色 | x叉 | v朝下三角符号 |
| -双划线 | c青色 | +加号 | ^朝上三角符号 |
| m品红 | *星号 | <朝左三角符号 | |
| y黄色 | >朝右三角符号 | p五角星 | |
| k黑色 | h六角星 | ||
| w白色 |
(2)图形的辅助标注和窗口的分割
title(图形说明)
xlabel(x轴说明)
ylabel(y轴说明)
text(x,y图形说明)——在x,y轴处添加文字说明
legend(图例一,图例二,…)
subplot(m,n,p)——将绘图区域分割成m*n个子区域,并按照行从左至 右,从上至下依次编号。p表示第p个绘图子区域。
注意:如果是要两个图画到同一个坐标里面,则在两个plot函数之间添加一行hold on
(3)格式
plot(x)——缺省自变量绘图格式
plot(x,y)——基本格式。以y(x)的函数关系作图。如果y是n*m的矩 阵,则x为自变量,作出m条曲线。
plot(x1,y1,x2,y2,…,xn,yn)——多条曲线绘图格式
plot(x1,y1,选项1,x2,y2,选项2,…,xn,yn,选项n)——含选项的绘图格式
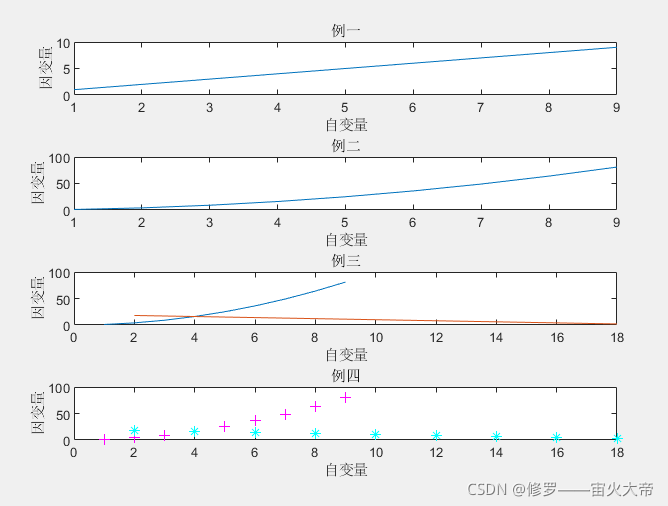
x1=[1 2 3 4 5 6 7 8 9];
x2=[2 4 6 8 10 12 14 16 18];
y1=[1 4 9 16 25 36 49 64 81];
y2=[18 16 14 12 10 8 6 4 2];
subplot(4,1,1);plot(x1);title('例一');xlabel('自变量');ylabel('因变量');
subplot(4,1,2);plot(x1,y1);title('例二');xlabel('自变量');ylabel('因变量');
subplot(4,1,3);plot(x1,y1,x2,y2);title('例三');xlabel('自变量');ylabel('因变量');
subplot(4,1,4);plot(x1,y1,'m+',x2,y2,'c*');title('例四');xlabel('自变量');ylabel('因变量');
2.三维图形
(1)格式
plot3(x1,y1,z1,‘选项一’,x2,y2,z1,‘选项二’,…)
x,y,z是长度相同的向量:一条曲线
x,y,z是维度相同的矩阵:多条曲线
(2)网格矩阵生成函数:meshgrid
[X,Y]=meshgrid(x,y)
x,y是给定的向量,X,Y是网格划分后得到的网格矩阵
注意,这个函数用来生成网格矩阵,不是直接用来画图的,配合mesh使用。
(3)mesh函数
mesh(X,Y,Z,C)
X,Y:网格坐标矩阵
Z:网格点上的高度矩阵
C:确定不同高度下的颜色范围
meshc:在mesh基础上增加等高线。
meshz:在mesh基础上增加底座。
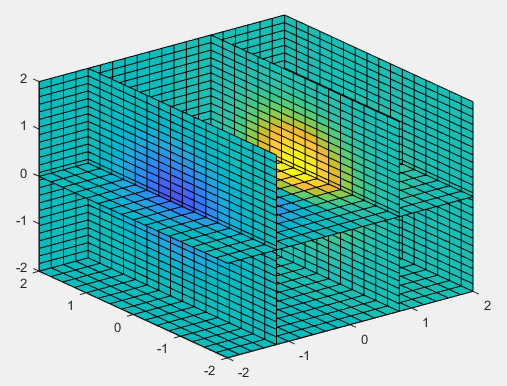
(4)surf函数
surf(X,Y,Z,C)——绘制由矩阵X,Y,Z确定的着色的三维表面图,参数含义同mesh
surfc——与surf相同,在此基础上增加等高线
surfl——与surf相同,在此基础上增加光照效果
注意:使用surfl的时候,C为一个二维或者三维向量。表示光源与曲面之间的方位。
x1=[1 2 3 4 5 6 7 8 9];
x2=[2 4 6 8 10 12 14 16 18];
z1=[1 2 3 4 5 6 7 8 9];
y1=[1 4 9 16 25 36 49 64 81];
y2=[18 16 14 12 10 8 6 4 2];
z2=[1 2 3 4 5 6 7 8 9];
Z=[1 2 3 4 5 6 7 8 9;2 3 4 5 6 7 8 9 10;3 4 5 6 7 8 9 10 11;4 5 6 7 8 9 10 11 12;5 6 7 8 9 10 11 12 13;6 7 8 9 10 11 12 13 14;7 8 9 10 11 12 13 14 15;8 9 10 11 12 13 14 15 16;9 10 11 12 13 14 15 16 17];
s=[40;60];
subplot(2,3,1);plot3(x1,y1,z1,x2,y2,z2);
subplot(2,3,2);[X,Y]=meshgrid(x1,y1);mesh(X,Y,Z,Z);
subplot(2,3,3);meshc(X,Y,Z,Z);
subplot(2,3,4);meshz(X,Y,Z,Z);
subplot(2,3,5);surfc(X,Y,Z,Z);
subplot(2,3,6);surfl(X,Y,Z,s);

二、特殊图形
1.对数坐标图
semilogx(x,y):x轴对数刻度,y轴线性刻度。
semilogy(x,y):x轴线性刻度,y轴对数刻度。
loglog(x,y):x,y都是对数刻度。
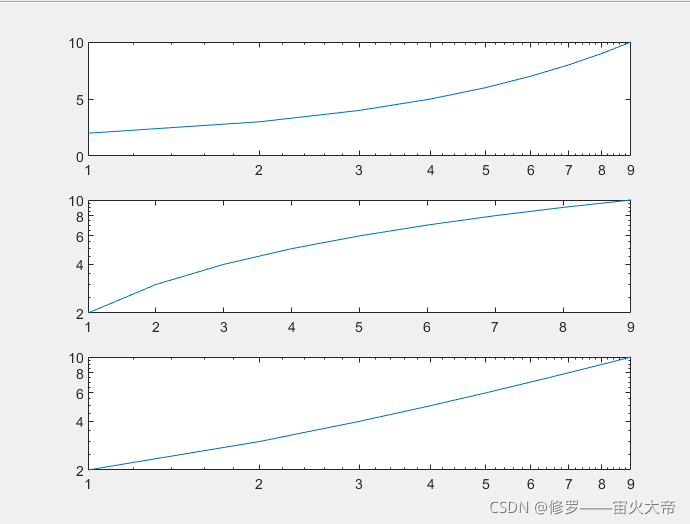
x=[1 2 3 4 5 6 7 8 9];
y=[2 3 4 5 6 7 8 9 10];
subplot(3,1,1);semilogx(x,y);
subplot(3,1,2);semilogy(x,y);
subplot(3,1,3);loglog(x,y);
2.极坐标图
polarplot (x,y): 在极坐标中绘制线条
polarscatter (x,y):极坐标中的散点图
polarhistogram (x,y) : 极坐标中的直方图(y为一个整数)
compass (x,y): 绘制从原点发射出的箭头
ezpolar (‘函数’):易用的极坐标绘图函数

x=[0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9];
y=[0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.10];
subplot(3,2,1);polarplot(x,y);
subplot(3,2,2);polarscatter(x,y);
subplot(3,2,3);polarhistogram(x,6);
subplot(3,2,4);compass(x,y);
subplot(3,2,5);ezpolar('1+2*sin(x)');
3.条形图
bar(y)——若y为向量,则分别显示每个分量的高度。若为矩阵,则把y分解为行向量,在分别画出。
bar(x,y)——在指定的横坐标x上画出y。x为单增向量。
bar(…,width)——设置条形的相对宽度和控制在一组内条形的间距,默认值为0.8。
bar(…,‘style’)——指定条形的排列类型。类型有“group”和“stack”。
group:若y为n*m矩阵,则bar显示n组,每组m个条形图
stack:对矩阵的每一个行向量显示在一个条形中,条形的高度为该行向量中的分量和,其中同一条形中的每个向量用不同的颜色显示出来,从而可以显示每个向量中的分布。
三维格式为bar3
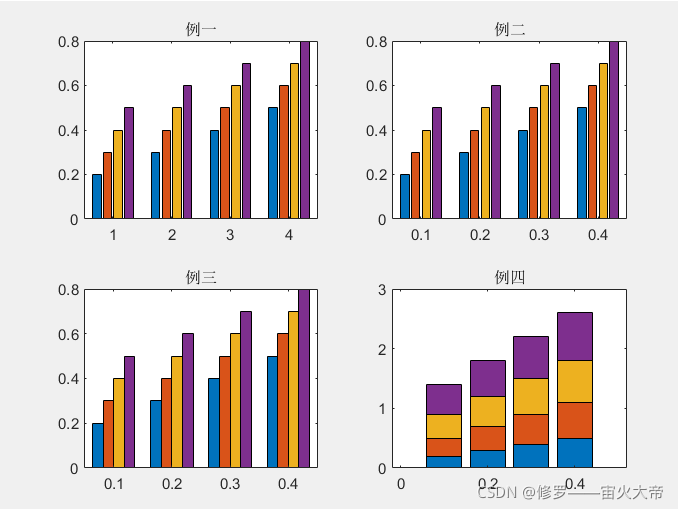
x=[0.1 0.2 0.3 0.4];
y=[0.1 1.1 5.4 3.4 2.3 4.5 3.2 3.4 5.6];
c=x+x';
subplot(2,2,1);bar(c);title('例一');
subplot(2,2,2);bar(x,c);title('例二');
subplot(2,2,3);bar(x,c,1);title('例三');
subplot(2,2,4);bar(x,c,'stack');title('例四');
4.面积图
area(x)——与plot(x)一样,但是将所得的曲线下方的区域填充颜色。
area(x,y)——y为向量,与plot(x,y)一样,但是将所得的曲线下方的区域填充颜色。
area(x,A)——矩阵A的第一行对向量x绘图,然后依次是下一行所有行值的和对向量x绘图,每个区域有各自的颜色。
area(…,leval)——将填色部分改为由连线图到y=leval的水平之间的部分。
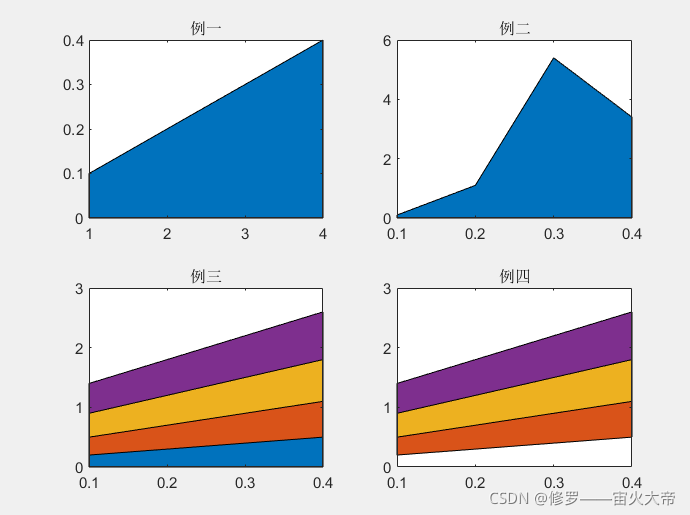
x=[0.1 0.2 0.3 0.4];
y=[0.1 1.1 5.4 3.4];
c=x+x';
subplot(2,2,1);area(x);title('例一');
subplot(2,2,2);area(x,y);title('例二');
subplot(2,2,3);area(x,c);title('例三');
subplot(2,2,4);area(x,c,1);title('例四');
5.饼状图
pie(x)——用x中的数据画一个饼状图。x中的每一个元素代表饼状图中的一部分。
pie(x,explode)——从饼状图中分离出一部分,explode是与x同维的矩阵。当所有元素为零时,饼状图各部分连一起组成一个圆。当其中有非零元时,元素对应的扇形往外移。
三维格式为pie3
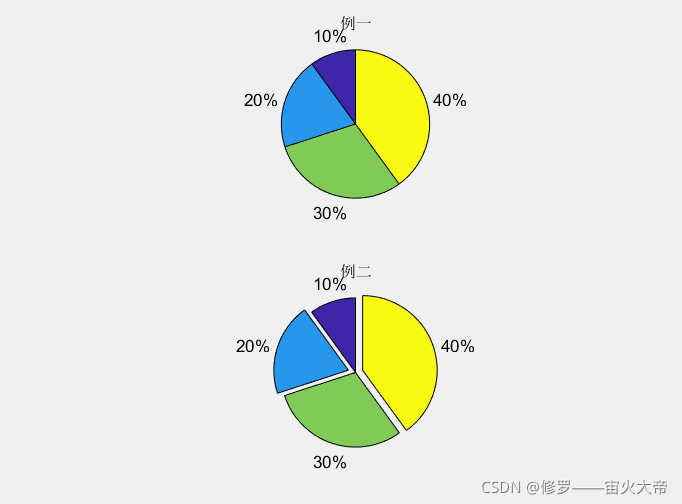
x=[0.1 0.2 0.3 0.4];
y=[0 1 0 1];
subplot(2,1,1);pie(x);title('例一');
subplot(2,1,2);pie(x,y);title('例二');
6.双y轴
yyaxis left——坐标轴在左边
yyaxis right——坐标轴在右边
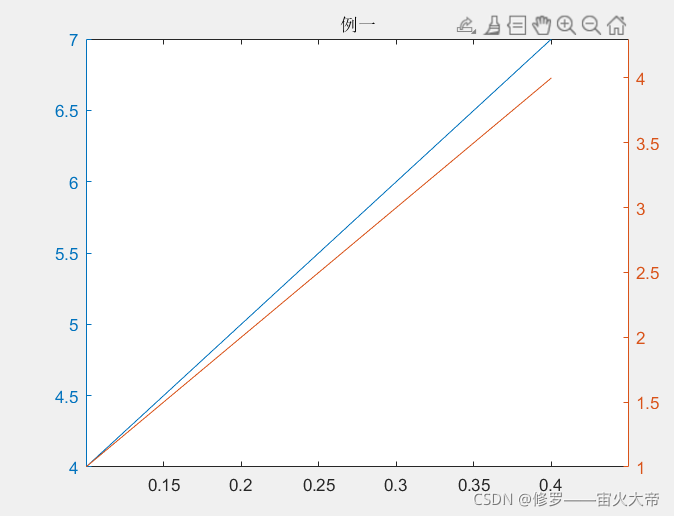
x=[0.1 0.2 0.3 0.4];
y1=[4 5 6 7];
y2=[1 2 3 4];
yyaxis left;
plot(x,y1);
yyaxis right;
plot(x,y2);
title('例一');
7.罗盘图
compass(x,y)——x,y为n维向量
compass(z)——z为n维复数向量
compass(x,y,选项)——选项为箭头的颜色,线型等。
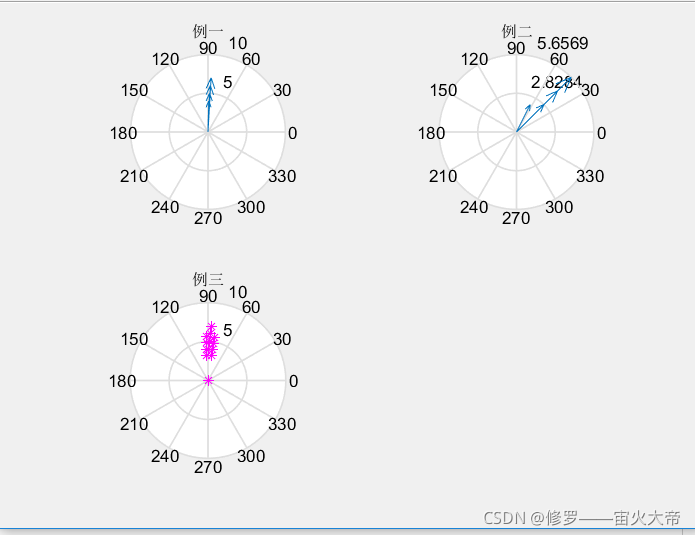
x=[0.1 0.2 0.3 0.4];
y=[4 5 6 7];
z=[1+2*i 2+2*i 3+3*i 4+4*i];
subplot(2,2,1);compass(x,y);title('例一');
subplot(2,2,2);compass(z);title('例二');
subplot(2,2,3);compass(x,y,'m*');title('例三');
8.羽毛图
feather函数
用法与罗盘图相同
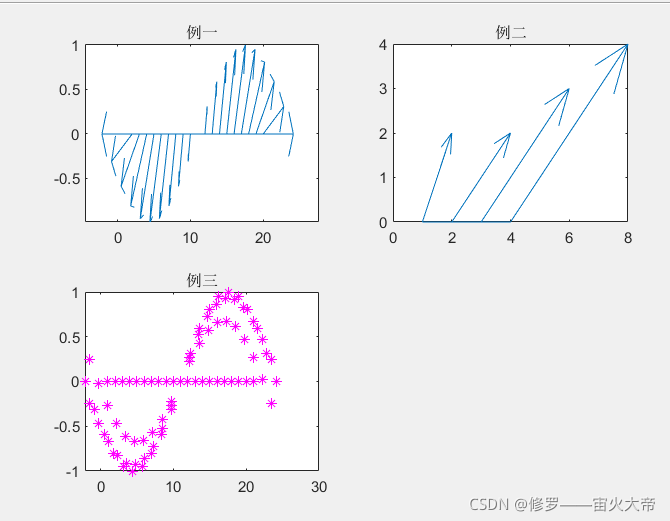
x=-pi:pi/10:pi;
y=sin(x);
z=[1+2*i 2+2*i 3+3*i 4+4*i];
subplot(2,2,1);feather(x,y);title('例一');
subplot(2,2,2);feather(z);title('例二');
subplot(2,2,3);feather(x,y,'m*');title('例三');
9.矢量图
quiver(u,v)——v为mn矩阵,绘出在范围x=1:n,y=1:m的坐标系中由u和v定义的向量
quiver(x,y,u,v)——x为n维向量,y为m维向量。u和v为mn维矩阵。则画出由x,y确定的每一个由u和v定义的向量。
quiver(…,scale)——对向量的长度进行处理。
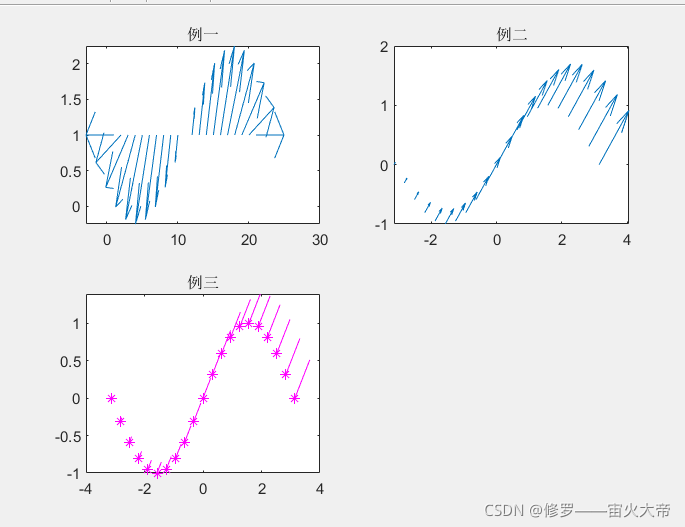
x=-pi:pi/10:pi;
y=sin(x);
for i=1:1:21u(i)=i;v(i)=i;
end
subplot(2,2,1);quiver(x,y);title('例一');
subplot(2,2,2);quiver(x,y,u,v);title('例二');
subplot(2,2,3);quiver(x,y,u,v,0.5,'m*');title('例三');
10.散点图
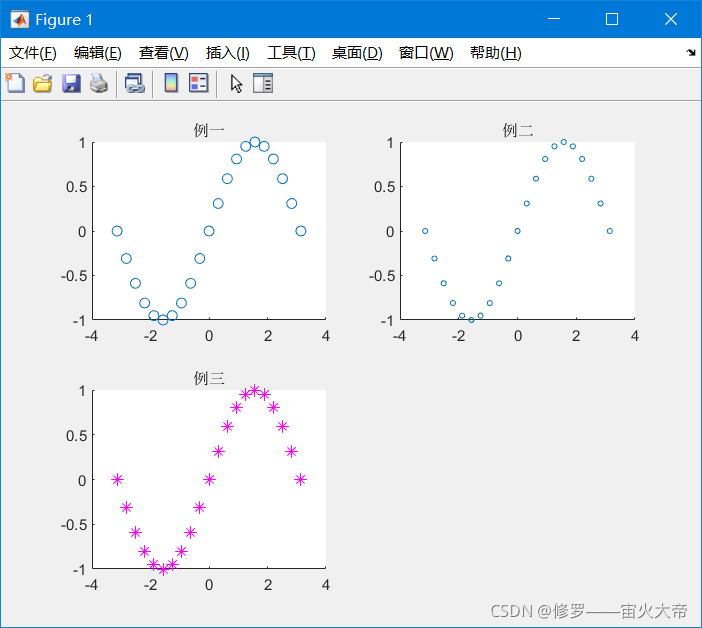
scatter(x,y)——x,y为向量,且长度相同。
scatter(x,y,sz)——sz标记面积,默认36。
scatter(x,y,sz,c)——c标记颜色。
x=-pi:pi/10:pi;
y=sin(x);
for i=1:1:21u(i)=i;v(i)=i;
end
subplot(2,2,1);scatter(x,y);title('例一');
subplot(2,2,2);scatter(x,y,10);title('例二');
subplot(2,2,3);scatter(x,y,50,'m*');title('例三');
总结
本文参考了很多其他的文章,这也是我第一次写,有写的不好的地方希望大家多提提意见。另外,本文也是当成笔记来写的,因此有一些地方写的很简洁,希望大家多多包涵。
参考
1.MATLAB中特殊图形的绘制
2.使用matlab绘制条形图、面积图、饼图、柱状图
3.【MATLAB】MATLAB 可视化之极坐标图
4.MATLAB 画图,对数坐标轴
5.数学建模之MATLAB画图汇总
6.Matlab绘图方法整理(超完整版)
7.如何使用Matlab绘制各类特殊图形