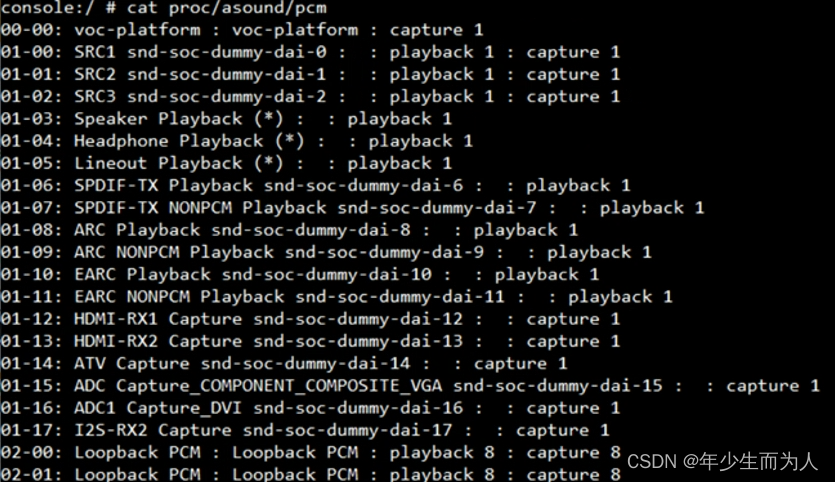
[对偶专题——Duality and Dual problem (一) https://blog.csdn.net/jmh1996/article/details/85030323]
对于一般的带约束的优化问题：

介绍了如何通过构造原优化目标的一个下界函数$L(x,\lambda ,u)$，这一般通过添加一些线性的函数来构造的，然后找到这个函数的最大值。寻找的方法是先固定$\lambda$ 最小化 $L(x,\lambda )$得到一个$g(\lambda ,u)$。然后再通过变化$\lambda ,u$的值来最大化$g(\lambda ,u)$。注意其中的一个重要的不等式：
$$f_0(x)\ge L(x,\lambda ,u)\ge g(\lambda ,u)$$
$g(\lambda ,u)$就是对偶函数，而最大化$g(\lambda ,u)$ 就是所谓的对偶问题。

原函数的图像与$L(x,\lambda ,u)$ 的图像是这样的：

我们可以看到，对于一般的最优化问题，原函数的最小值其实和$L(x,\lambda ,u)$的最大值是存在一段距离的，他们并不相等。

如果他们相等的话，那么我们就可以通过解对偶问题来求原目标函数的最小值，可以想象这会给问题求解带来巨大的便利，因为对偶函数 $always$ 是个凸函数。

那么什么时候下对偶问题的最大值会等于原问题的最小值呢？

我们先看只有等式约束的情况：

现在只含有等式约束，其实是方便的很了。

假设$f_0(x,y)和h(x,y)=0$的图像是这样的：

如上图所示，红线是$h(x,y)=0$ 这个等式确定的一条曲线。各个蓝圈圈是$f_0(x,y)=1,2,3\cdot \cdot \cdot$形成的曲线。现在，我们观察到当$f_0(x,y)=2$ 的时候，$f_0(x,y)$ 与$h(x,y)=0$ 相交于两个点，此时目测当$f_0(x,y)$继续变小的时候，它和$h(x,y)=0$ 依然还有交点，因此$2$ 肯定就不是$f_0(x,y)$的最小值。当$f_0(x,y)=1$的时候，它和$h(x,y)=0$ 只有一个交点了，交点是两个曲线的切点处，$f_0(x,y)$ 再变小一点点 它就和红线没有交点了，因此$f_0(x,y)$ 的最小值就是1。假设交点是$(x^{\ast },y^{\ast })$。

注意到$f_0(x,y)=1$ 与 $h(x,y)=0$ 相切于$(x^{\ast },y^{\ast })$，根据相切的定义我们可以得到它们的梯度是共线的：$▽f_0(x,y)=\lambda ▽h(x,y)$。

于是，对于带等式约束$h(x)=0$ 的最优化问题，我们可以得到。