2021SC@SDUSC

Dust3D中的材质采用PBR模型。PBR就是Physically-Based Rendering的缩写，意为基于物理的渲染。它提供了一种光照和渲染方法，能够更精确的描绘光和表面之间的作用。由于PBR基于物理的渲染旨在以物理上合理的方式模拟光，因此与我们的原始照明算法（如 Phong 和 Blinn-Phong）相比，它通常看起来更逼真。因为它非常接近实际物理，我们可以根据物理参数创作表面材料。它不仅擅长用来表现非常写实的材质，同时也能用来处理风格化的资源。

文章目录

Microfacet Model
Energy Conservation
反射方程
BRDF
菲涅尔方程
PBR材质

Microfacet Model

现实当中大多数物体的表面都会有非常微小的缺陷：微小的凹槽、裂缝、几乎肉眼不可见的凸起，以及在正常情况下过于细小以至于难以使用普通映射表现出来的细节。尽管这些微观的细节几乎难以用肉眼观察到，但是他们仍然影响着光的扩散和反射。
微表面处的细节对反射的影响最容易被观察到，当平行光照射到粗糙表面时会分散开来，也即是每条光线都照射到了物体表面上朝向不同的部分，导致更广泛的镜面反射。
在这里插入图片描述

没有任何表面在微观层面上是完全光滑的，但由于这些微表面足够小，我们无法在每个像素的基础上区分它们，但我们在统计上近似表面的微表面粗糙度，给定粗糙度范围。基于表面的粗糙度，我们可以计算出与某个向量大致对齐的微表面的比率 h。这个向量 h 是个半程向量(Halfway Vector)，即光线与视线夹角一半方向上的一个单位向量：

微表面的细节对于任何材质都是个非常重要的特质，就像真实世界中就有着各种各样的微表面。光泽度贴图并不是一个新概念，但因为微表面的细节对光照的反射具有如此重要的影响，所以它在PBR中占据了一个关键位置。所有的 PBR 技术都基于微平面理论。该理论描述了任何微观尺度的表面都可以用微小的完全反射镜来描述，称为微表面。根据表面的粗糙度，这些微小的镜面的对齐方式可能会有很大差异。

Energy Conservation

如果每个像素的镜面反射强度相同（无论镜面反射形状的大小如何），则较粗糙的表面会因为具有更多像素的微表面而发出更多的能量，这违反能量守恒原理，所以在光滑的表面上看到的镜面反射更强烈，而在粗糙的表面上则更暗淡。光线照射到表面的那一刻，会分成一个折射部分和一个反射部分，折射部分是进入表面并被吸收的剩余光，反射部分是直接被反射而不进入表面的光。

在这里插入图片描述
从物理学中，我们知道光可以被描述为一束能量，它不断向前移动直到失去所有能量。光束失去能量的方式是碰撞。一般来说，并不是所有的能量都被吸收，大部分光会继续分散在随机方向上，与其他粒子碰撞直到它的能量耗尽或再次离开表面。从表面重新出现的光线对人眼观察到的表面颜色有贡献。在PBR中，我们假设所有折射光都会在非常小的影响区域被吸收和散射，忽略从远处离开表面的散射光线的影响——这一技术称为次表面散射，他可以显著改善皮肤、大理石或蜡等材料的视觉质量，但会以性能为代价。

金属表面遵循相同的反射和折射原理，但所有折射光都被直接吸收而不会散射。这意味着金属表面只留下反射光或镜面光，而不显示漫反射光。由于金属和非金属之间的这种明显区别，它们在 PBR 中的处理方式不同。

我们首先通过计算反射、入射光能量百分比的镜面反射率来保持能量守恒关系。然后根据镜面反射率直接计算折射光的分数。这样我们既知道入射光的反射量，也知道入射光的折射量，同时遵守能量守恒原理。鉴于这种方法，折射/漫射和反射/镜面反射的贡献不可能超过1.0，这可以确保它们的能量总和永远不会超过入射光能量。

float kS = calculateSpecularComponent(...); // reflection/specular fraction
float kD = 1.0 - kS;                        // refraction/diffuse  fraction

vec4 evaluateLightMaterialColor(in vec4 normal)
{// 初始化为黑色vec3 finalColor = vec3(c_zero, c_zero, c_zero);// 将黑色更新为基础环境色finalColor += qt_Light.ambient.rgb * qt_Material.ambient.rgb;// 添加漫反射组件vec4 lightDir = vec4( normalize(qt_Light.direction), 0.0 );float diffuseFactor = max( c_zero, dot(lightDir, normal) );if(diffuseFactor > c_zero){finalColor += qt_Light.diffuse.rgb *qt_Material.diffuse.rgb *diffuseFactor *qt_Material.brightness;}// 添加镜面反射组件const vec3 blackColor = vec3(c_zero, c_zero, c_zero);if( !(qt_Material.specular.rgb == blackColor || qt_Light.specular.rgb == blackColor || qt_Material.specularPower == c_zero) ){vec4 viewDir = vec4( normalize(qt_Light.eye), 0.0 );vec4 reflectionVec = reflect(lightDir, normal);float specularFactor = max( c_zero, dot(reflectionVec, -viewDir) );if(specularFactor > c_zero){specularFactor = pow( specularFactor, qt_Material.specularPower );finalColor += qt_Light.specular.rgb *qt_Material.specular.rgb *specularFactor;}}return vec4( finalColor, qt_Material.opacity );
}

反射方程

反射方程基于辐照度，它是以点 p 为中心的半球 Ω 内的测量光的所有入射辐射的总和。

在这里插入图片描述

int steps = 100;
float sum = 0.0f;
vec3 P    = ...;
vec3 Wo   = ...;
vec3 N    = ...;
float dW  = 1.0f / steps;
for(int i = 0; i < steps; ++i) 
{vec3 Wi = getNextIncomingLightDir(i);sum += Fr(P, Wi, Wo) * L(P, Wi) * dot(N, Wi) * dW;
}

如果我们认为立体角 ω 和面积 A 无限小，我们可以使用辐射度来测量照射到空间中的某一点的单束光线。这使我们能够计算影响单个点的单个光线的辐射，将立体角 ω 转换为方向向量 ω，将 A 转换为点 p。这样，我们可以直接在着色器中使用辐射来计算单个光线对每个片段的贡献。
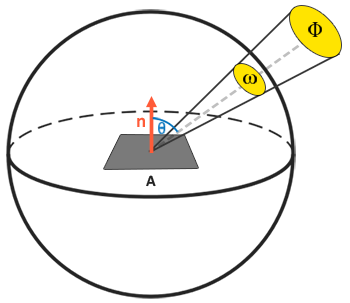
在这里插入图片描述

BRDF

BRDF即双向反射分布函数，是一个将入射光方向 ω_i 、出射光方向 ω_o 、表面法线 n 和表示微表面粗糙度的表面参数 a 作为输入的函数。 BRDF 近似于每个单独的光线 ω_i 对具有材料属性的不透明表面的最终反射光的贡献程度。例如，如果表面有一个绝对光滑的表面，BRDF 函数将为所有入射光线 ω_i 返回 0，除了与出射光线 ω_o 具有相同（反射）角度的一条光线，函数在该光线处返回 1 。

BRDF 近似于基于微平面理论的材料的反射和折射特性。为了使 BRDF 在物理上合理，它必须遵守能量守恒定律，即反射光的总和不应超过入射光的量。从技术上讲，Blinn-Phong 被认为是采用相同的 ω_i 和 ω_o 作为输入的 BRDF。然而，Blinn-Phong 不被认为是基于物理的，因为它不遵守能量守恒原理。有几种基于物理的 BRDF 来近似表面对光的反应。但是，几乎所有实时 PBR 渲染管线都使用称为 Cook-Torrance BRDF 的 BRDF。

Cook-Torrance BRDF 包含漫反射和镜面反射部分：
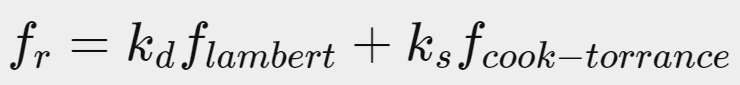
在这里插入图片描述

菲涅尔方程

菲涅尔方程描述了反射光与折射光的比率，折射光会随我们观察的角度变化而变化。光线照射到表面时，根据表面到视角的角度，可以计算出被反射的光的百分比。根据这个反射比和能量守恒原理，我们可以直接得到光的折射部分。

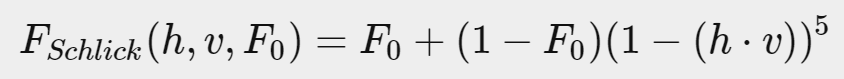
在这里插入图片描述

vec3 fresnelFactor(const in vec3 color, const in float cosineFactor)
{// 计算菲涅耳效应值vec3 f = color;vec3 F = f + (1.0 - f) * pow(1.0 - cosineFactor, 5.0);return clamp(F, f, vec3(1.0));
}

PBR材质

PBR 所需的每个表面参数都可以通过纹理定义。使用纹理让我们可以局部控制每个特定的表面点对光的反应：该点是金属的、粗糙的还是光滑的，或者表面如何不同波长的光。

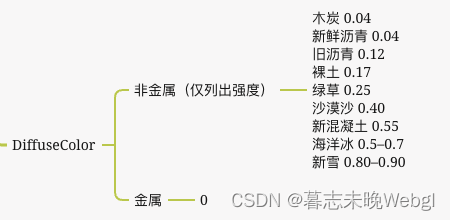
Albedo：Albedo 纹理为每个纹素指定表面的颜色，如果该纹素是金属的，则指定基础反射率。这在很大程度上类似于漫反射纹理，但所有光照信息都是从纹理中提取的。漫反射纹理通常在图像内部有轻微的阴影或变暗的裂缝，但这是我们不希望在 Albedo 纹理中看到的，它应该只包含表面的颜色（或折射吸收系数）。

Normal：法线贴图纹理允许我们为每个片段指定一个独特的法线，以产生表面比其平坦对应物更颠簸的错觉。

Metallic：金属贴图指定每个纹素是金属还是非金属。根据 PBR 的设置方式，可以将金属度设置为灰度值或二进制黑色或白色。

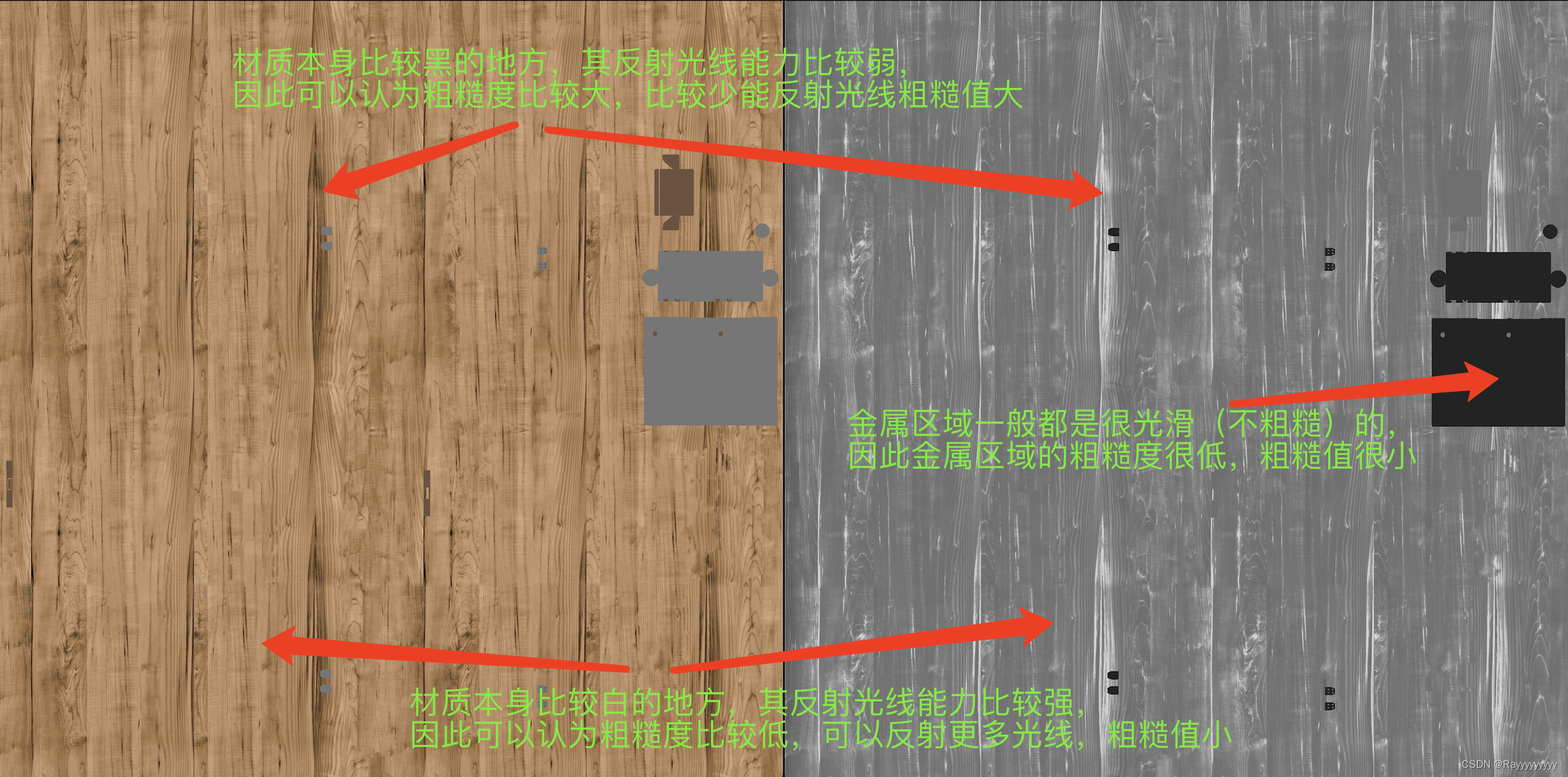
Roughness：粗糙度贴图指定表面在每个纹素基础上的粗糙度。粗糙度的采样粗糙度值影响表面的统计微面取向。粗糙的表面会产生更广泛和更模糊的反射，而光滑的表面会产生聚焦和清晰的反射。

AO : 环境光遮蔽/AO贴图指定了表面和潜在周围几何体的额外阴影因素。例如，如果我们有一个砖块表面，在砖块的缝隙内应该没有阴影信息。然而，AO 贴图指定了这些边缘处的阴影。

vec3 pbrModel(const in int lightIndex,const in vec3 wPosition,const in vec3 wNormal,const in vec3 wView,const in vec3 baseColor,const in float metalness,const in float alpha,const in float ambientOcclusion)
{vec3 n = wNormal;vec3 s = vec3(0.0);vec3 v = wView;vec3 h = vec3(0.0);float vDotN = dot(v, n);float sDotN = 0.0;float sDotH = 0.0;float att = 1.0;if (lights[lightIndex].type != TYPE_DIRECTIONAL) {// 点光源和聚光灯vec3 sUnnormalized = vec3(lights[lightIndex].position) - wPosition;s = normalize(sUnnormalized);// 计算衰减因子sDotN = dot(s, n);if (sDotN > 0.0) {if (lights[lightIndex].constantAttenuation != 0.0|| lights[lightIndex].linearAttenuation != 0.0|| lights[lightIndex].quadraticAttenuation != 0.0) {float dist = length(sUnnormalized);att = 1.0 / (lights[lightIndex].constantAttenuation +lights[lightIndex].linearAttenuation * dist +lights[lightIndex].quadraticAttenuation * dist * dist);}// 光线的方向已经转换到世界空间中if (lights[lightIndex].type == TYPE_SPOT) {// 检查片段是在聚光灯锥的内部还是外部if (degrees(acos(dot(-s, lights[lightIndex].direction))) > lights[lightIndex].cutOffAngle)sDotN = 0.0;}}} else {// 定向光源// 光线的方向已经转换到世界空间中s = normalize(-lights[lightIndex].direction);sDotN = dot(s, n);}h = normalize(s + v);sDotH = dot(s, h);// 计算漫反射分量vec3 diffuseColor = (1.0 - metalness) * baseColor * lights[lightIndex].color;vec3 diffuse = diffuseColor * max(sDotN, 0.0) / 3.14159;// 计算镜面反射分量vec3 dielectricColor = vec3(0.04);vec3 F0 = mix(dielectricColor, baseColor, metalness);vec3 specularFactor = vec3(0.0);if (sDotN > 0.0) {specularFactor = specularModel(F0, sDotH, sDotN, vDotN, n, h);specularFactor *= normalDistribution(n, h, alpha);}vec3 specularColor = lights[lightIndex].color;vec3 specular = specularColor * specularFactor;// 混合漫反射和镜面反射vec3 color = att * lights[lightIndex].intensity * (specular + diffuse * (vec3(1.0) - specular));// 环境遮挡量衰减color *= ambientOcclusion;return color;
}