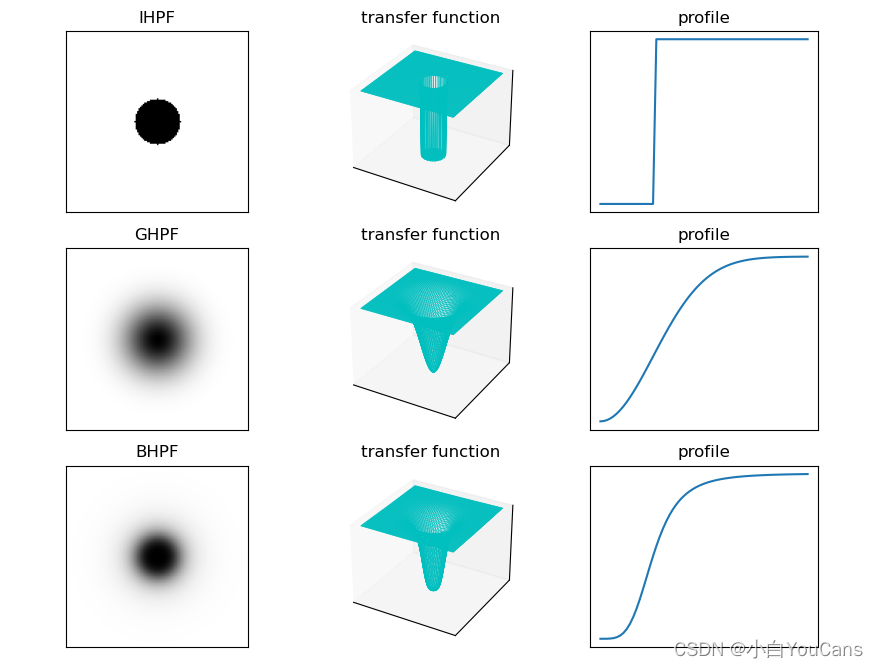
频域高通滤波

高通滤波器的功能是削弱或消除低频分量而保留高频分量。

理想高通滤波器

理想低通滤波器，模拟上容易实现，物理上无法实现。

转移函数定义：
$$H(u,v)=\{\begin{array}{rl}& 0，D(u,v)<=D_0\\ & 1，D(u,v)>D_0\end{array}$$

巴特沃斯高通滤波器

巴特沃斯低通滤波器是物理上可实现的,高低频之间的过渡比较平滑。

转移函数定义为:

$$H(u,v)=\frac{1}{1+[\frac{D_0}{D(u,v)}{]}^{2n}}$$

高斯高通滤波器

$$H(u,v)=1-e^{\frac{-{D(u,v)}^2}{2{D_0}^2}}$$

Opencv低通滤波

import cv2 as cv
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

img = cv.imread('./images/kunting.png')
img = cv.cvtColor(img, cv.COLOR_BGR2RGB)
img_gray = cv.cvtColor(img, cv.COLOR_RGB2GRAY)

测试用例（美剧《杀出个黎明》）：

傅里叶变换:

dft = cv.dft(img_gray.astype('float32'),flags = cv.DFT_COMPLEX_OUTPUT)           # 傅里叶变换(Opencv是用深度为2数组表示复数)
dft_shift = np.fft.fftshift(dft)                                                 # 移动零频分量
magnitude_spectrum = cv.magnitude(dft_shift[:,:,0], dft_shift[:,:,1])
log_magnitude_spectrum = 20*np.log(magnitude_spectrum)  # 幅值对数变换

理想、巴特沃斯、高斯HPF

def hpf(dft_shift, r=100):m, n, _ = dft_shift.shapecenter = (m//2, n//2)mask = np.zeros_like(dft_shift)x_arr = np.concatenate([np.arange(m).reshape(m, 1)], axis=1)y_arr = np.concatenate([np.arange(n).reshape(1, n)], axis=0)dist = np.sqrt((x_arr - center[0])**2 + (y_arr - center[1])**2)mask[dist > r] = 1return maskdef bw_hpf(dft_shift, r=100, N=1):m, n, _ = dft_shift.shapecenter = (m//2, n//2)mask = np.ones_like(dft_shift)x_arr = np.concatenate([np.arange(m).reshape(m, 1)], axis=1)y_arr = np.concatenate([np.arange(n).reshape(1, n)], axis=0)dist = np.sqrt((x_arr - center[0])**2 + (y_arr - center[1])**2).reshape(m, n, 1)+0.01mask = 1/(1+(r/dist)**(2*N))return maskdef gaussian_hpf(dft_shift, r=100):m, n, _ = dft_shift.shapecenter = (m//2, n//2)x_arr = np.concatenate([np.arange(m).reshape(m, 1)], axis=1)y_arr = np.concatenate([np.arange(n).reshape(1, n)], axis=0)dist_square = np.sqrt((x_arr - center[0])**2 + (y_arr - center[1])**2).reshape(m, n, 1)mask = 1-np.exp(-1*dist_square/(2*r*r))return mask

huv = hpf(dft_shift, r=50)                        # 转移函数（算子/模)
hpf_dft_shift = dft_shift * huv                # 低通滤波
hpf_magnitude_spectrum = cv.magnitude(hpf_dft_shift[:,:,0], hpf_dft_shift[:,:,1])
log_hpf_magnitude_spectrum = 20*np.log(hpf_magnitude_spectrum+1) # 幅值对数变换
hpf_dft = np.fft.ifftshift(hpf_dft_shift)         # 还原频谱图
img_ = cv.idft(hpf_dft)                           # 逆傅里叶变换
img_hpf1 = cv.magnitude (img_[:,:,0],img_[:,:,1])  # 还原图像

边缘检测的效果。

sobel_x、sobel_y、scharr算子对低频的抑制

scharr = np.array([[-3, 0, 3],[-10,0,10],[-3, 0, 3]])
# sobel in x direction
sobel_x= np.array([[-1, 0, 1],[-2, 0, 2],[-1, 0, 1]])
# sobel in y direction
sobel_y= np.array([[-1,-2,-1],[0, 0, 0],[1, 2, 1]])

高通滤波同时保留部分低频分量：

$$G_e(u,v)=G(u,v)+cF(u,v)，0<c<1$$

$c=0.5$：

huv = hpf(dft_shift, r=50)                         
hpf_dft_shift = dft_shift * huv + 0.5*dft_shift   # 高通滤波 + c*低频分量
hpf_dft = np.fft.ifftshift(hpf_dft_shift)          
img_ = cv.idft(hpf_dft)                            
img_hpf_a = cv.magnitude (img_[:,:,0],img_[:,:,1])   

不仅边缘得到了增强，整体图像信息也得到保留。