1. 加窗法设计滤波器

为什么要加窗设计滤波器？因为为了降低DFT的频率泄露。那什么是DFT频率泄露以及为什么加窗设计就可以降低DFT的频率泄露？解释这个之前，我们先介绍一下DFT（离散傅里叶变换）和三角函数的正交性知识，再介绍加窗设计的原因。

首先是DFT：
$$X(m)=\sum _{n=0}^{N-1}x(n)e^{-j2\pi nm/N}=\sum _{n=0}^{N-1}x(n)[cos(2\pi nm/N)-j(sin(2\pi nm/N)]$$
$X(m)$是第m个频率分量的幅值，$x(n)$是从连续变量$x(t)$中取样得到的一个离散时间序列的第n个值。
需要注意的是，这里的N是指对时域信号有。N是固定大小，常见的都是2的整数倍。如果N个离散采样点没有采样到完整的周期数时，那么输入的残缺部分的能量就会泄露到其他频率分量上。

下面是三角函数的正交性知识点，可以解释为什么周期不完整会造成频率泄露？（正交即内积运算值为零）
对于三角函数集 { 1 , c o s ( n Ω t ) , s i n ( m Ω t ) } \{1, cos(n\Omega t), sin(m\Omega t) \} {1,cos(nΩt),sin(mΩt)}，中有如下三条正交性性质：

• 任意频率成分的sin和cos函数正交
• 频率不相等的sin函数正交
• 频率不相等的cos函数正交

正交成立的前提是，函数的周期要完整。比如说，频率的sin和cos函数都只有第一象限部分的数据，那么他们的内积显然不为0。但是你不能因此说明这两个函数不正交。此处内积不为零的原因是你的采样点没有完整周期。 以下面例子说明，这个对时域信号投影到频域上的影响。

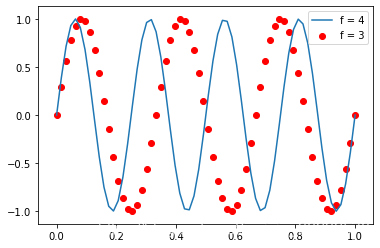
对于输入信号（f=3）采样正好取到完整周期时（红色圆点）。图中f=4是对比参照系，用来说明问题的。
输入信号f=3在频域理论上应该只有频率为3处有幅值。也就是说，再频率为4的地方$sin(2\pi 3t)$和$sin(2\pi 4t)$和$cos(2\pi 4t)$的内积应该为零。计算结果也正好是接近零。说明输入信号f=3在频率4处没有分量。

import numpy as np
n_vec = np.linspace(0, 1, 64)
ans = 0
for i in n_vec:ans += np.sin(2*np.pi*3*i)*np.sin(2*np.pi*4*i)
print(ans)plt.figure()
plt.plot(n_vec, np.sin(2*np.pi*4*n_vec))
plt.scatter(n_vec, np.sin(2*np.pi*3*n_vec), c='r')
plt.legend(['f = 4', 'f = 3'])
plt.show()

1.665334536937742e-16

图1 采样恰好是完整周期情况

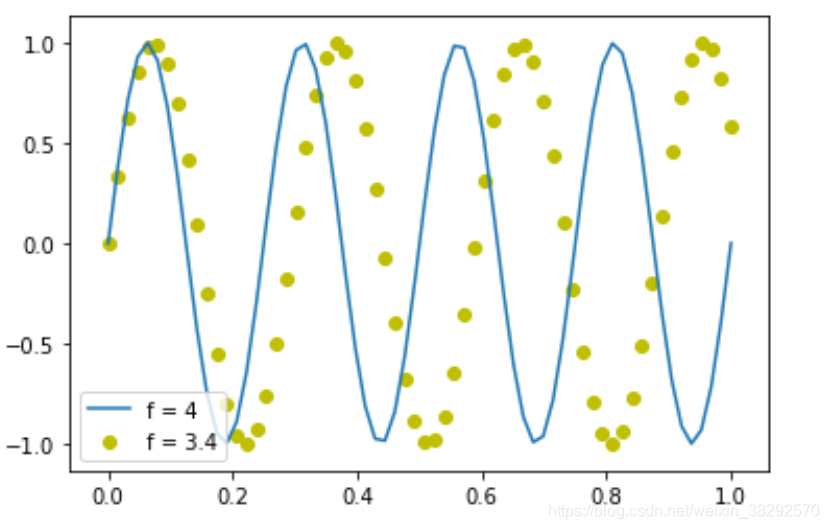
对于输入信号（f=3.4）采样没有取到完整周期时（黄色圆点）。图中f=4是对比参照系，用来说明问题的。
f=3.4这个信号，理论上在频域上应该只有频率为3.4处有幅值。也就是说$sin(2\pi 3.4t)$和$sin(2\pi 4t)$的内积应该零。
不为零就说明了在频率4处，输入信号f=3.4有幅值。即发生了频率泄露。
由前面正交性的介绍，我们知道这个不是因为非正交引起的，而是信号不完整引起的。

ans = 0
for i in n_vec:ans += np.sin(2*np.pi*3.4*i)*np.sin(2*np.pi*4*i)
print(ans)plt.figure()
plt.plot(n_vec, np.sin(2*np.pi*4*n_vec))
plt.scatter(n_vec, np.sin(2*np.pi*3.4*n_vec), c='y')
plt.legend(['f = 4', 'f = 3.4'])
plt.show()

-5.289826894417038

图2 采样不是完整周期情况

还有一种有关分析频率的说法， $f_{an}=\frac{m{f}_s}{N},m=0,1,2,..,N-1$，
如果$f_s=12000,N=1024$,那么$f_{an}=11.7m,m=0,1,2,...,1023$ ,如果输入信号频率是5Hz，正好位于两个相邻的分析频率之间（0和11.7），那么5Hz的信号会在所有频率分量上出现。可以理解为频率为分析频率的输入信号正好可以被N=1024个采样点可以取到完整周期。而$\frac{f_s}{N}$又被成为分辨率。

加窗法为什么可以降低频率泄露呢？逆向思考，从上述分析我们知道，要想减少频率泄露，只要尽量保证进行DFT计算的信号是接近完整周期即可（是尽量，无法完全做到）。窗函数就可以透过截取信号来做到这一点，以hamming窗为例。

# 信号频谱绘图函数
from scipy import signal
from scipy.fftpack import fft
def plot_freq(x, fs):N = len(x)T = 1/fsX = x - np.mean(x)yf = fft(X)xf = np.linspace(0.0, 1.0/(2.0*T), N//2)# 画图plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))# plt.xlim(0, 500)plt.title('Signal spectrum')plt.xlabel("frequency")plt.ylabel("amplitude")plt.grid()plt.show()

下面这个函数绘制不加窗情况下，f=3.4信号的FFT变换

import numpy as np
n_vec = np.linspace(0, 1, 64)
x = np.sin(2*np.pi*3.4*n_vec)
plt.figure(figsize=(5,6))
plt.subplot(2,1,1)
plt.scatter(n_vec, x, c='y')
plt.subplot(2,1,2)
plot_freq(x, 64)
plt.show()

图3 不加窗情况下，f=3.4信号的FFT变换，频率泄露

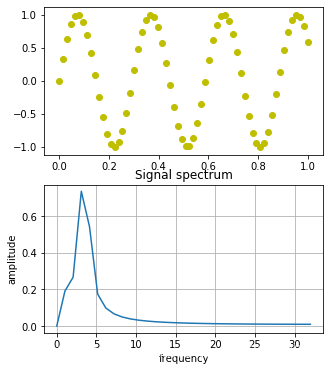
下面代码是加窗情况下，f=3.4信号的FFT变换

import numpy as np
n_vec = np.linspace(0, 1, 64)
win = np.hamming(64)
x = np.multiply(np.sin(2*np.pi*3.4*n_vec),win)
plt.figure(figsize=(5,6))
plt.subplot(2,1,1)
plt.scatter(n_vec, x, c='y')
plt.subplot(2,1,2)
plot_freq(x, 64)
plt.show()

图4 加窗情况下，f=3.4信号的FFT变换，频率泄露改善

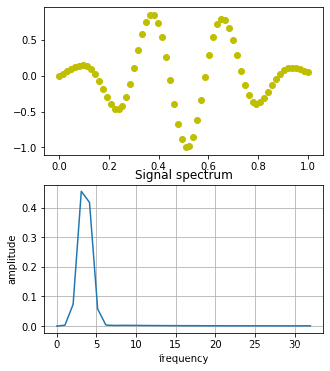
发现加了hamming窗的x信号变得更像周期信号。突然，意识到加窗真有点是“自欺欺人”（非贬义）的想法。不过，这算是一种工程近似办法，无法得到精确的，就寻找近似值。这种思想应用在很多领域，比如微分、积分的定义，所谓的无限逼近之前的部分就是一个粗糙的近似。

两幅图对比可以发现，加了汉明窗改善了频率泄露问题，使得频谱更加向3.4Hz靠拢。原因在于，hamming截取的信号部分比原来的采样信号，更接近一个完整的信号周期。于是，频率泄露的问题就得到了改善。（不是解决，也无法解决）

2. FIR加窗法设计高通滤波器

def plot_freqz_2(h, fs):w1, h1 = signal.freqz(h, fs=fs)plt.title('Digital filter frequency response')plt.plot(w1, 20*np.log10(np.abs(h1)), 'b')plt.ylabel('Amplitude Response (dB)')plt.xlabel('Frequency (rad/sample)')plt.grid()plt.show()

生成带噪声的信号xn：

# 生成信号：6kHz、100Hz， 10Hz，并且带有高斯噪声
t = np.linspace(0, 1, 12000)
x = np.sin(2*np.pi*5000*t) + np.sin(2*np.pi*100*t)*0.2+np.sin(2*np.pi*10*t)*0.1
xn = x + np.random.randn(len(t))
plt.figure()
plt.plot(t,x)
plt.plot(t,xn)
plt.legend(['x', 'xn'])
plt.xlim(0, 0.008)
plt.title('x and xn')
plt.xlabel("time/s")
plt.ylabel("amplitude")
plt.show()

图5 生成信号xn：6kHz、100Hz， 10Hz，并且带有高斯噪声

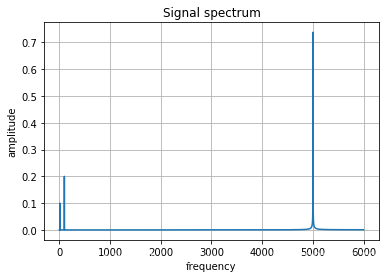
查看不带噪声信号和带噪声信号的频谱图。

# 不带噪声的信号频谱图
fs = 12000
plot_freq(x, fs)

图6-a 不带噪声的信号频谱图

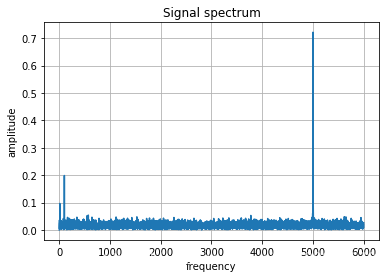
# 带噪声信号的频谱图
plot_freq(xn, fs)

图6-b 带噪声信号的频谱图

可见高斯随机噪声的频谱是遍布每个频率分量。

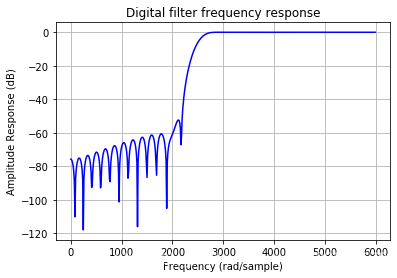
下面设计加窗的FIR高通滤波器，截止频率为2500Hz，可以滤掉xn中的低频，保留5000Hz的高频信号。并显示滤波器的幅频响应。

# FIR高通滤波器设计
fs = 12000
N = 64
fc = 2500
# 滤波器的最大响应频率是fs/2.这个是由奈奎斯特采样定理决定的
g_ = signal.firwin(N+1,fc,fs=fs, pass_zero='highpass')
plot_freqz_2(g_, fs)

图7

下面对带噪声信号分别进行滤波处理，并查看频谱图。

# 带噪声信号的滤波后频谱图
new_x = signal.convolve(xn, g_, mode='full')
plot_freq(new_x, fs)

图8 带噪声信号xn的滤波后频谱图

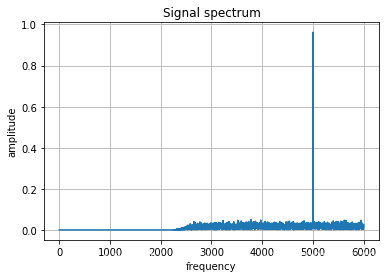
发现滤掉了低频信号，保留了高频部分，但是高频部分中的高斯噪声依旧保留着。