下面三种序列可以唯一的构造唯一的一棵二叉树:
前序序列和中序序列构造二叉树
后序序列和中序序列构造二叉树
层次遍历序列和中序遍历序列构造二叉树
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#define MaxSize 10
typedef struct BTNode{char data;struct BTNode *lchild,*rchild;
}BTNode,*BiTree;//根据前序序列,中序序列建造一棵二叉树
//参数含义:pre[]前序序列 in[]中序序列
// L1 R1用于指定pre[]的搜索区域
// L2 R2用于指定in[]的搜索区域
BiTree createBiTree(char pre[],char in[],int L1,int R1,int L2,int R2){if(L1>R1){return NULL;//递归出口 }BTNode *s =(BTNode*)malloc(sizeof(BTNode));s->lchild =NULL;s->rchild =NULL;s->data=pre[L1];int i;//根据中序序列的特性,元素左边的元素属于该节点的左孩子序列,右边则是右孩子序列 for(i=L2;i<=R2;i++){if(pre[L1]==in[i]) break;//在中序序列找到该元素 }s->lchild=createBiTree(pre,in,L1+1,L1+i-L2,L2,i-1);//递归 s->rchild=createBiTree(pre,in,L1+i-L2+1,R1,i+1,R2); return s;
}
//根据后序中序建立二叉树
BiTree createBiTree2(char post[],char in[],int L1,int R1,int L2,int R2){if(L1>R1){return NULL;//递归出口 }BTNode *s =(BTNode*)malloc(sizeof(BTNode));s->lchild =NULL;s->rchild =NULL; s->data=post[R1];//后序序列最后一个节点为根节点 int i;//根据中序序列的特性,元素左边的元素属于该节点的左孩子序列,右边则是右孩子序列 for(i=L2;i<=R2;i++){if(post[R1]==in[i]) break;//在中序序列找到该元素 }//递归 面试官:为什么要减去L2? 答:递归传下去的是整个数组,需要根据参数找到递归出口,-L2是缩小查找范围 s->lchild=createBiTree2(post,in,L1,L1+i-L2-1,L2,i-1);s->rchild=createBiTree2(post,in,L1+i-L2,R1-1,i+1,R2); return s;
}
//该函数用于在中序序列中找到key,返回其位置
//参数含义:in[]:中序序列 key:所要查找元素 L,R:查找范围
int serach(char in[],char key,int L,int R){for(int i=L;i<=R;i++){if(in[i]==key) return i;}return -1;
}//因为在中序序列元素的左面的元素在层次遍历序列中并不连续,所以需要用子序列函数将并不连续的序列连续起来
//为什么要连续起来?因为需要连续起来才能和中序序列构造出二叉树
//思路:在中序序列里查找到一个范围,从这个范围里遍历元素,在层次遍历序列里找该元素
//参数含义:sublevel[]:存放子序列数组 level[]:层次遍历序列 in[]:中序序列 n:level层次序列长度 L,R:查找范围
void getSubLevel(char sublevel[],char level[],char in[],int n,int L,int R){int k=0;for(int i=0;i<n;i++){if(serach(in,level[i],L,R)!=-1)sublevel[k++]=level[i]; }
}
//由中序序列和层次遍历序列构造二叉树
BiTree createBiTree3(char level[],char in[],int n,int L,int R){if(L>R) return NULL;BTNode *s =(BTNode*)malloc(sizeof(BTNode));s->lchild =NULL;s->rchild =NULL; s->data=level[0];int i=serach(in,level[0],L,R);//找到i便可以确定左右子树答大小 int LN=i-L; char LLevel[LN];int RN=R-i; char RLevel[RN];getSubLevel(LLevel,level,in,n,L,i-1);//得到子序列 getSubLevel(RLevel,level,in,n,i+1,R);s->lchild=createBiTree3(LLevel,in,LN,L,i-1);//用子序列递归 s->rchild=createBiTree3(RLevel,in,RN,i+1,R); return s;
}
void visit(BiTree T) {printf("%c ",T->data);
}
//前序遍历
void PreOrder(BiTree T){if(T!=NULL){visit(T);//根 PreOrder(T->lchild);//左 PreOrder(T->rchild);//右 }
}
//中序遍历
void InOrder(BiTree T){if(T!=NULL){InOrder(T->lchild);visit(T);InOrder(T->rchild);}
}
//后序遍历
void PostOrder(BiTree T){if(T!=NULL){PostOrder(T->lchild);PostOrder(T->rchild);visit(T);}
}
//层次遍历
void level(BiTree T){if(T!=NULL){int front=0;int rear=0;BiTree queue[MaxSize];BiTree p;p=T;rear=(rear+1)%MaxSize;queue[rear]=p;while(rear!=front){front=(front+1)%MaxSize;p=queue[front];visit(p); if(p->lchild!=NULL){rear=(rear+1)%MaxSize;queue[rear]=p->lchild; } if(p->rchild!=NULL){rear=(rear+1)%MaxSize;queue[rear]=p->rchild;}}}
}
int main(){char c[]="ABDECFGH";//前序序列 char d[]="DBEACGFH";//中序序列 char p[]="DEBGHFCA";//后序序列 char l[]="ABCDEFGH";//层次遍历序列 BTNode *r=createBiTree(c,d,0,7,0,7);BTNode *r2=createBiTree2(p,d,0,7,0,7);BTNode *r3=createBiTree3(l,d,8,0,7); printf("前序序列为:"); PreOrder(r);printf("\n");printf("后序序列为:");PostOrder(r2);printf("\n");printf("中序序列为:"); InOrder(r3);printf("\n");printf("层次遍历为:");level(r3); printf("\n");} 代码运行截图:




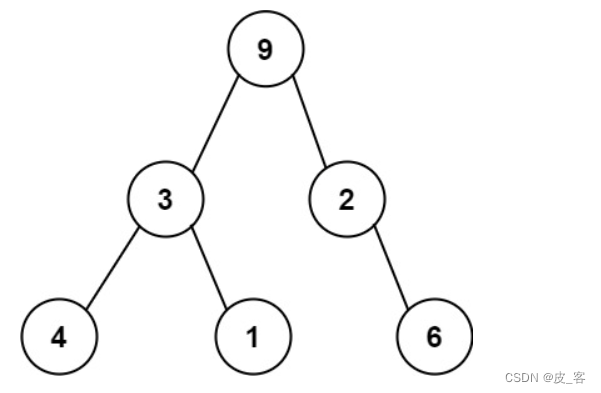
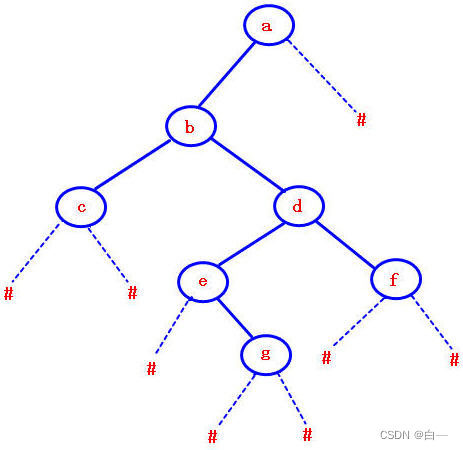
![IIC通信协议详解[转载]](https://img-blog.csdnimg.cn/20190210172036333.jpg?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzM4NDEwNzMw,size_16,color_FFFFFF,t_70)