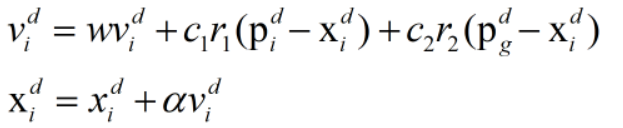粒子群算法详解

一.产生背景

❃粒子群算法(particleswarm optimization，PSO)由Kennedy和Eberhart在1995年提出，该算法对于Hepper的模拟鸟群(鱼群)的模型进行修正，以使粒子能够飞向解空间，并在最好解处降落，从而得到了粒子群优化算法。

❃同遗传算法类似，也是一种基于群体叠代的，但并没有遗传算法用的交叉以及变异，而是粒子在解空间追随最优的粒子进行搜索。

❃PSO的优势在于简单，容易实现，无需梯度信息，参数少，特别是其天然的实数编码特点特别适合于处理实优化问题。同时又有深刻的智能背景，既适合科学研究，又特别适合工程应用。

设想这样一个场景：一群鸟在随机的搜索食物。在这个区域里只有一块食物，所有的鸟都不知道食物在哪。但是它们知道自己当前的位置距离食物还有多远。

那么找到食物的最优策略是什么？

最简单有效的就是搜寻目前离食物最近的鸟的周围区域。

二.算法介绍

(1)简述

❃每个寻优的问题解都被想像成一只鸟，称为“粒子”。所有粒子都在一个D维空间进行搜索。

❃所有的粒子都由一个fitness-function确定适应值以判断目前的位置好坏。

❃每一个粒子必须赋予记忆功能，能记住所搜寻到的最佳位置。

❃每一个粒子还有一个速度以决定飞行的距离和方向。这个速度根据它本身的飞行经验以及同伴的飞行经验进行动态调整。

(2) 基本PSO算法

a. D维空间中，有m个粒子；

粒子i位置：xi=(xi1,xi2,…xiD)

粒子i速度：vi=(vi1,vi2,…viD)，1≤i≤m,1 ≤d ≤D

粒子i经历过的历史最好位置：pi=(pi1,pi2,…piD)

群体内（或领域内）所有粒子所经历过的最好位置：

pg =(pg1,pg2,…pgD)

PS:一般来说，粒子的位置和速度都是在连续的实数空间内进行取值。

b.基本PSO公式

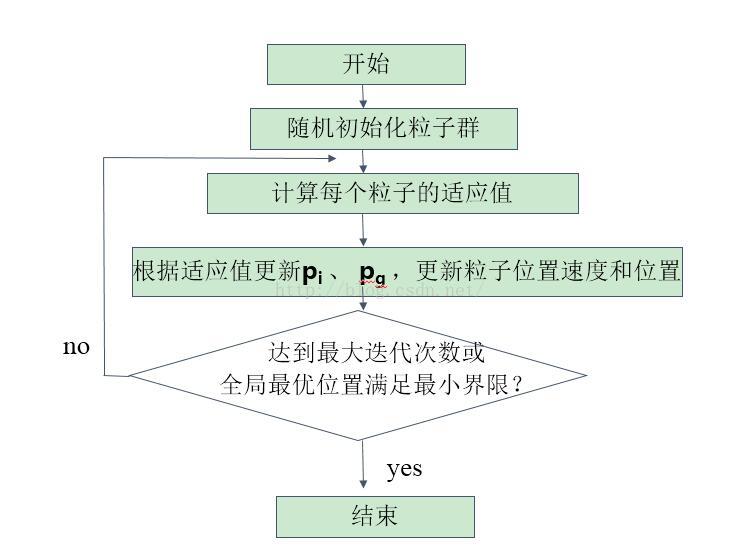
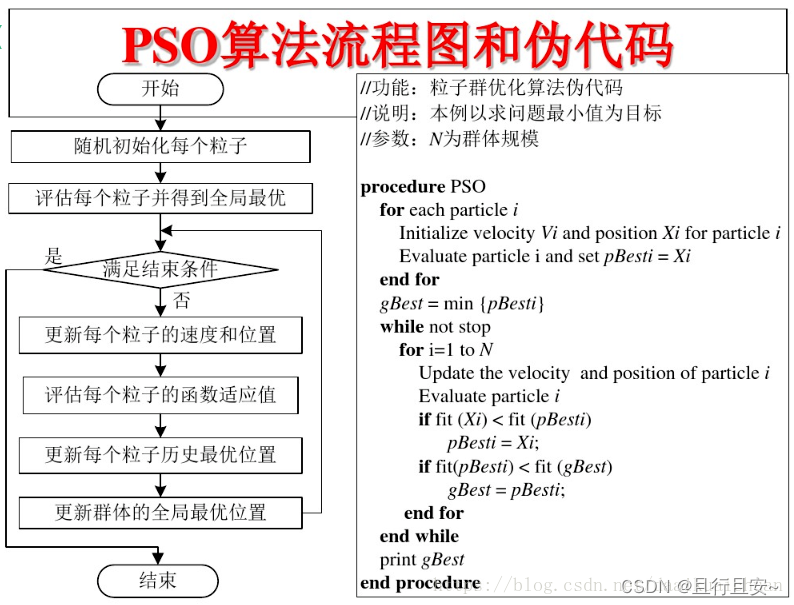
(3)基本PSO算法流程图

关于每个粒子的更新速度和位置的公式如下:

三.简单应用

(1)•编码：因为问题的维数为5，所以每个粒子为5维的实数向量。

(2)•初始化范围：根据问题要求，设定为[-30，30]。根据前面的参数分析，我们知道，可以将最大速度设定为Vmax=60。

(3)•种群大小：为了说明方便，这里采用一个较小的种群规模，m=5。

(4)•停止准则：设定为最大迭代次数100次。

(5)•惯性权重：采用固定权重0.5。

(6)邻域拓扑结构：使用星形拓扑结构，即全局版本的粒子群优化算法

算法执行的过程如下:

四.代码实现:运用粒子群算法解决 TSP问题

1.matlab实现

close all;
clear all;PopSize=500;%种群大小
CityNum = 14;%城市数OldBestFitness=0;%旧的最优适应度值Iteration=0;%迭代次数
MaxIteration =2000;%最大迭代次数
IsStop=0;%程序停止标志 
Num=0;%取得相同适应度值的迭代次数c1=0.5;%认知系数
c2=0.7;%社会学习系数
w=0.96-Iteration/MaxIteration;%惯性系数,随迭代次数增加而递减%节点坐标
node=[16.47 96.10; 16.47 94.44; 20.09 92.54; 22.39 93.37; 25.23 97.24;...22.00 96.05; 20.47 97.02; 17.20 96.29; 16.30 97.38; 14.05 98.12;...16.53 97.38; 21.52 95.59; 19.41 97.13; 20.09 94.55];%初始化各粒子，即产生路径种群
Group=ones(CityNum,PopSize);   
for i=1:PopSizeGroup(:,i)=randperm(CityNum)';
end
Group=Arrange(Group);%初始化粒子速度（即交换序）
Velocity =zeros(CityNum,PopSize);   
for i=1:PopSizeVelocity(:,i)=round(rand(1,CityNum)'*CityNum); %round取整
end%计算每个城市之间的距离
CityBetweenDistance=zeros(CityNum,CityNum);   
for i=1:CityNumfor j=1:CityNumCityBetweenDistance(i,j)=sqrt((node(i,1)-node(j,1))^2+(node(i,2)-node(j,2))^2);end
end%计算每条路径的距离
for i=1:PopSize   EachPathDis(i) = PathDistance(Group(:,i)',CityBetweenDistance);
endIndivdualBest=Group;%记录各粒子的个体极值点位置,即个体找到的最短路径
IndivdualBestFitness=EachPathDis;%记录最佳适应度值,即个体找到的最短路径的长度
[GlobalBestFitness,index]=min(EachPathDis);%找出全局最优值和相应序号 %初始随机解
figure;
subplot(2,2,1);
PathPlot(node,CityNum,index,IndivdualBest);
title('随机解');%寻优
while(IsStop == 0) & (Iteration < MaxIteration) %迭代次数递增Iteration = Iteration +1;  %更新全局极值点位置,这里指路径for i=1:PopSize   GlobalBest(:,i) = Group(:,index);end%求pij-xij ,pgj-xij交换序，并以概率c1，c2的保留交换序pij_xij=GenerateChangeNums(Group,IndivdualBest);  pij_xij=HoldByOdds(pij_xij,c1); pgj_xij=GenerateChangeNums(Group,GlobalBest);pgj_xij=HoldByOdds(pgj_xij,c2);%以概率w保留上一代交换序Velocity=HoldByOdds(Velocity,w);Group = PathExchange(Group,Velocity); %根据交换序进行路径交换Group = PathExchange(Group,pij_xij);Group = PathExchange(Group,pgj_xij);for i = 1:PopSize    % 更新各路径总距离EachPathDis(i) = PathDistance(Group(:,i)',CityBetweenDistance);endIsChange = EachPathDis<IndivdualBestFitness;%更新后的距离优于更新前的，记录序号IndivdualBest(:, find(IsChange)) = Group(:, find(IsChange));%更新个体最佳路径IndivdualBestFitness = IndivdualBestFitness.*( ~IsChange) + EachPathDis.*IsChange;%更新个体最佳路径距离[GlobalBestFitness, index] = min(EachPathDis);%更新全局最佳路径,记录相应的序号if GlobalBestFitness==OldBestFitness %比较更新前和更新后的适应度值;Num=Num+1; %相等时记录加一;elseOldBestFitness=GlobalBestFitness;%不相等时更新适应度值，并记录清零;Num=0;end    if Num >= 20 %多次迭代的适应度值相近时程序停止IsStop=1;endBestFitness(Iteration) =GlobalBestFitness;%每一代的最优适应度end%最优解
subplot(2,2,2);
PathPlot(node,CityNum,index,IndivdualBest);
title('优化解');
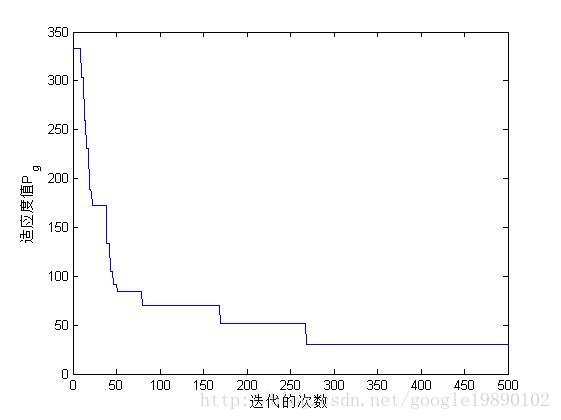
%进化曲线
subplot(2,2,3);
plot((1:Iteration),BestFitness(1:Iteration));
grid on;
title('进化曲线');
%最小路径值
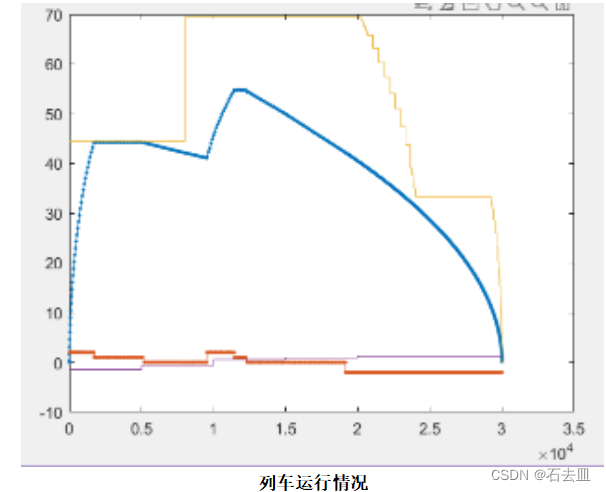
GlobalBestFitness运行结果如下:

2.java 实现

package pso;
import java.awt.*;
import java.awt.event.*;
import java.io.ByteArrayInputStream;
import java.io.InputStream;import javax.swing.*;
import javax.swing.event.*;
public class Pso extends Frame implements Runnable
{private static int particleNumber;  //粒子的数量private static int iterations;      //迭代的次数private static int k=1;             //记录迭代的次数final private static float C1=2;    //学习因子final private static float C2=2;final private static float WMIN=-200;final private static float WMAX=200;final private static float VMAX=200;private static float r1;           //随机数0-1之间private static float r2;private static float x[][];private static float v[][];private static float xpbest[][];private static float pbest[];      private static float gbest=0;private static float xgbest[];private static float w;           //惯性因子private static float s;private static float h;private static float fit[];public Sounds sound;//粒子群的迭代函数
public void lzqjs()
{w=(float)(0.9-k*(0.9-0.4)/iterations);for(int i=0;i<particleNumber;i++){fit[i]= (float)(1/(Math.pow(x[i][0],2)+Math.pow(x[i][1],2))); //求适值函数最大值System.out.print("粒子"+i+"本次适应值函数f为：" + fit[i]);System.out.println();if(fit[i]>pbest[i]){pbest[i]=fit[i];xpbest[i][0]=x[i][0];xpbest[i][1]=x[i][1];}if(pbest[i]>gbest){gbest=pbest[i];xgbest[0]=xpbest[i][0];xgbest[1]=xpbest[i][1];}}for(int i=0;i<particleNumber;i++){for(int j=0;j<2;j++){//粒子速度和位置迭代方程:v[i][j]=(float)(w*v[i][j]+C1*Math.random()*(xpbest[i][j]-x[i][j])+C2*Math.random()*(xgbest[j]-x[i][j]));x[i][j]=(float)(x[i][j]+v[i][j]);}System.out.print("粒子"+i+"本次X1的速度变化幅度:"+v[i][0]+";本次X2的速度变化幅度:"+v[i][1]);System.out.println();System.out.print("粒子"+i+"本次X1为："+x[i][0]+";本次X2为："+x[i][1]);System.out.println();}
}public static void main(String[] args){particleNumber=Integer.parseInt(JOptionPane.showInputDialog("请输入粒子个数1-500）"));iterations=Integer.parseInt(JOptionPane.showInputDialog("请输入迭代次数"));x=new float [particleNumber][2];v=new float [particleNumber][2];fit=new float [particleNumber];    //存储适值函数值pbest=new float [particleNumber];  //存储整个粒子群的最有位置xpbest=new float [particleNumber][2];xgbest=new float [2];for(int i=0;i<particleNumber;i++){//对数组的初始化操作pbest[i]=0;xpbest[i][0]=0;xpbest[i][1]=0;}xgbest[0]=0;xgbest[1]=0;System.out.println("开始初始化：");for(int i=0;i<particleNumber;i++){for(int j=0;j<2;j++){//任意给定每个位置一定的位置值和速度值x[i][j]=(float)(WMAX*Math.random()+WMIN);v[i][j]=(float)(VMAX*Math.random());}System.out.print("粒子"+i+"本次X1的变化幅度:"+v[i][0]+";本次X2的变化幅度:"+v[i][1]);System.out.println();System.out.print("粒子"+i+"本次X1为："+x[i][0]+";本次X2为："+x[i][1]);System.out.println();}System.out.println("初始化数据结束，开始迭代.....");Pso threada=new Pso();threada.setTitle("基于粒子群的粒子位置动态显示");threada.setSize(800,800);threada.addWindowListener(new gbck());threada.setVisible(true);Thread threadc=new Thread(threada);threadc.start();}static class gbck extends WindowAdapter{public void windowClosing(WindowEvent e){System.exit(0);}}//开启的额外线程用于声音的播放public void run(){repaint();for(int i=0;i<iterations;i++){sound();}}public void paint(Graphics g){g.setColor(new Color(0,0,0));for(int i=0;i<particleNumber;i++){g.drawString("*",(int)(x[i][0]+200),(int)(x[i][1]+200));}g.setColor(new Color(255,0,0));g.drawString("全局最优适应度函数值："+gbest+"      参数1："+xgbest[0]+"     参数2："+xgbest[1]+"    迭代次数："+ k,50,725);try{lzqjs();  //开始迭代if(k>=iterations){Thread.sleep((int)(5000));System.exit(0);}k=k+1;  //每次迭代一次加1操作Thread.sleep((int)(1000));}catch(InterruptedException e){System.out.println(e.toString());}repaint();}public  void sound(){sound =new Sounds("050.wav");InputStream stream =new ByteArrayInputStream(sound.getSamples());// play the soundsound.play(stream);// exit}
}

运行的结果如下: