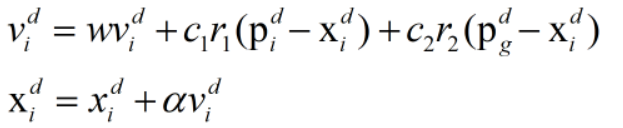背景
1995 年,Kennedy 和 Eberhart 两位博士共同 提出了粒子群优化算法 (Particle swarm optimization, PSO) PSO 算法中,将鸟群的个体位置或食物当作优化问题的解,利用群体中个体与最优个体以及个体之间的信息交互,引导整个群体中个体在保留自身多样性信息的同时,朝向群体最优个体收敛,通过不断地更新逐渐找到最优解.
算法原理
通俗的说,就是有一群鸟儿在寻找食物,每只鸟都在不断改变自己的位置及速度。当任何一只鸟发现了有一个地方食物非常的多后,就会将信息告诉其他的鸟儿,其他的鸟儿在收到信息过后,怎样移动呢?
假设t时刻有一个编号为i鸟,它已经搜索了许多地方,其中自己遇到的食物最多的地方为Pbesti,与此同时种群中的其它鸟报告了一个当前发现食物最多的位置Gbest(t),Gbest(t)位置食物量更多,见下图

牛顿告诉我们,物体是有惯性的,v1即为鸟i在t时刻的运动方向,v2是朝向鸟i自己曾经到达过的食物最多的位置的方向的速度,v3则为群体发现的最好位置的方向,最终的v为三个方向的速度合的作用,使得鸟儿在下一时刻t+1到达位置xi+1
不直接让鸟i飞向群体最优位置Gbest是为了防止种群过快收敛,即实现引导整个群体中个体在保留自身多样性信息的同时,朝向群体最优个体收敛。这样可以尽可能的发现更多更好的位置。防止由于收敛过快而导致“早熟”。
了解基本原理,再看数学公式就很简单了

vi,t即为t时刻鸟i的速度(矢量),ω为惯性权重,c1,c2分别为分别为自身认识学习速度和社会学习速度的学习因子,rand1 i 和 rand2i 为随机因子,在 0 和 1 之间随机取值.xi,t为为t时刻鸟i的速度,xi,t+1为更新后的位置。
根据经验,通常随算法的不断迭代,惯性权重应该逐渐减小,自我学习因子减小,社会学习因子要逐渐变大,实际使用过程中需要根据实际情况设置函数进行控制。
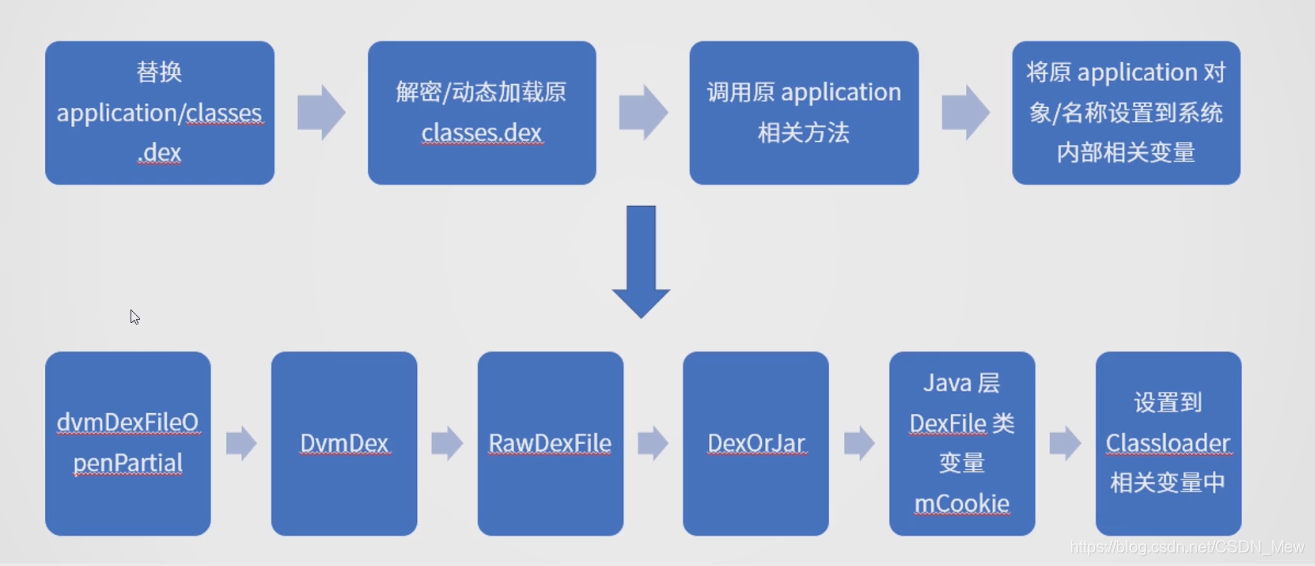
流程
优化算法的流程图如下,图片来源于网络,侵删